Probar la hipótesis mediante una prueba T
Importante
El soporte técnico de Machine Learning Studio (clásico) finalizará el 31 de agosto de 2024. Se recomienda realizar la transición a Azure Machine Learning antes de esa fecha.
A partir del 1 de diciembre de 2021 no se podrán crear recursos de Machine Learning Studio (clásico). Hasta el 31 de agosto de 2024, puede seguir usando los recursos de Machine Learning Studio (clásico) existentes.
- Consulte la información acerca de traslado de proyectos de aprendizaje automático de ML Studio (clásico) a Azure Machine Learning.
- Más información sobre Azure Machine Learning.
La documentación de ML Studio (clásico) se está retirando y es posible que no se actualice en el futuro.
Compara los medios de dos columnas mediante una prueba t
Categoría: Funciones estadísticas
Nota
Se aplica a: solo Machine Learning Studio (clásico)
Hay módulos para arrastrar y colocar similares en el diseñador de Azure Machine Learning.
Información general sobre el módulo
En este artículo se describe cómo usar el módulo Hipótesis de prueba mediante t-Test en Machine Learning Studio (clásico) para generar puntuaciones para tres tipos de pruebas t:
- Prueba t de muestra única
- Prueba t relacionada
- Prueba t independiente
En general, la prueba t le permite comparar si dos grupos tienen medias diferentes. Por ejemplo, supongamos que está evaluando los datos de las pruebas de los pacientes que recibieron el fármaco A en comparación con los pacientes que recibieron el fármaco B y necesita comparar una métrica de velocidad de recuperación en ambos grupos. La hipótesis nula supondría que la velocidad de recuperación es la misma en ambos grupos y, además, que los valores de velocidad de recuperación tienen una distribución normal en los dos grupos.
Mediante el uso de hipótesis de prueba mediante t-Test y proporcionar las columnas que contienen las tasas de recuperación como entrada, puede obtener puntuaciones que indican si la diferencia es significativa, lo que significaría que se debe rechazar la hipótesis nula. La prueba tiene en cuenta factores como el tamaño de la diferencia entre los valores, el tamaño de la muestra (mayor es mejor) y el tamaño de la desviación estándar (menor es mejor).
Al revisar los resultados del módulo Hipótesis de prueba mediante t-Test , puede determinar si la hipótesis nula es TRUE o FALSE y revisar las puntuaciones de confianza (P) de la prueba t.
Cómo elegir una prueba t
Elija una prueba t de ejemplo única cuando se apliquen estas condiciones:
Tiene una única muestra de puntuaciones.
Todas las puntuaciones son independientes entre sí.
La distribución de muestreo de xˉ es normal.
En general, la prueba t de muestra única se usa para comparar un valor promedio con un número conocido.
Elija una prueba t emparejada cuando se apliquen estas condiciones:
Tiene un par coincidente de resultados. Por ejemplo, puede que tenga dos medidas distintas por persona o pares coincidentes de personas, como marido y mujer.
Cada par de puntuaciones es independiente del resto de pares.
La distribución de muestreo de d es normal.
La prueba t relacionada es útil para comparar casos relacionados. Al calcular el promedio de las diferencias entre las puntuaciones de los casos emparejados, puede averiguar si la diferencia total es estadísticamente significativa.
Elija una prueba t sin emparejar cuando se apliquen estas condiciones:
Tiene dos muestras independientes de puntuaciones. Es decir, no hay ningún motivo para emparejar las puntuaciones de la muestra 1 con las de la muestra 2.
Todas las puntuaciones de una muestra son independientes entre sí.
La distribución de muestreo de x1- x2 es normal.
Opcionalmente, puede cumplir el requisito de que la varianza entre los grupos sea aproximadamente la misma.
Configuración de hipótesis de prueba mediante t-Test
Use un único conjunto de datos como entrada. Las columnas que se comparan deben estar en el mismo conjunto de datos.
Si necesita comparar columnas de distintos conjuntos de datos, puede aislar cada columna para compararla mediante Seleccionar columnas en el conjunto de datos y, a continuación, combinarlas en un conjunto de datos mediante Agregar columnas.
Agregue el módulo Hipótesis de prueba mediante t-Test al experimento.
Puede encontrar este módulo en la categoría Funciones estadísticas de Studio (clásico).
Agregue el conjunto de datos que contiene la columna o columnas que desea analizar.
Decida qué tipo de prueba t es adecuada para los datos. Consulte Cómo elegir una prueba t.
Ejemplo único: si usa un solo ejemplo, establezca estos parámetros:
Null hipótesis μ: escriba el valor que se va a usar como media hipotética de null para la muestra. Especifica el valor medio esperado con el que se probará la media de muestra.
Columna de destino: use el selector de columnas para elegir una sola columna numérica para las pruebas.
Tipo de hipótesis: elija una prueba de una cola o de dos colas. El valor predeterminado es una prueba de dos colas. Es el tipo más común de prueba, en el que las distribuciones son simétricas alrededor del cero.
La opción One Tail GT es para un valor de una cola mayor que la prueba. Esta prueba proporciona más potencia para detectar un efecto en una dirección, sin probar el efecto en la otra dirección.
La opción One Tail LT proporciona una cola inferior a la prueba.
α: especifique un factor de confianza. Este valor se usa para evaluar el valor de P (la primera salida del módulo). Si p es menor que el factor de confianza, se rechaza la hipótesis nula.
PairedSamples: si va a comparar dos ejemplos de la misma población, establezca estos parámetros:
Null hipótesis μ: escriba un valor que represente la diferencia de ejemplo entre el par de muestras.
Columna de destino: use el Selector de columnas para elegir las dos columnas numéricas que se van a probar.
Tipo de hipótesis: seleccione una prueba de una cola o de dos colas. El valor predeterminado es una prueba de dos colas.
α: especifique el factor de confianza. Este valor se usa para evaluar el valor de P (la primera salida del módulo)> Si p es menor que el factor de confianza, se rechaza la hipótesis nula.
Un aparejadoSamples: si compara dos ejemplos no emparejados, establezca estos parámetros:
- Suponga que la varianza es igual: anule la selección de esta opción cuando las muestras sean de diferentes poblaciones.
- Null hipótesis μ1: escriba la media para la primera columna.
- Null hipótesis μ2: escriba la media para la segunda columna.
- Columnas de destino: use el selector de columnas para elegir dos columnas numéricas que se van a probar.
- Tipo de hipótesis: indica si la prueba es de una cola o de dos colas. El valor predeterminado es una prueba de dos colas.
- α: especifique el factor de confianza. Este valor se usa para evaluar el valor de P (la primera salida del módulo)> Si p es menor que el factor de confianza, se rechaza la hipótesis nula.
Ejecute el experimento.
Results
La salida del módulo es un conjunto de datos que contiene las puntuaciones de prueba t y una transformación que, opcionalmente, puede guardar para volver a aplicar a este conjunto de datos u otro conjunto de datos mediante Aplicar transformación.
El conjunto de datos de puntuaciones contiene estos valores, independientemente del tipo de prueba t que usó:
- Una puntuación de probabilidad que indica la confianza de la hipótesis nula
- Un valor que indica si se debe rechazar la hipótesis nula
Sugerencia
Recuerde que el objetivo es determinar si puede rechazar la hipótesis nula. Una puntuación de 0 no significa que debe aceptar la hipótesis nula: significa que no tiene suficientes datos y necesita una investigación más detallada.
Notas técnicas
El módulo nombra automáticamente las columnas de salida según las convenciones siguientes, dependiendo del tipo de prueba t seleccionada y de si el resultado fue rechazar o aceptar la hipótesis nula.
Dadas las columnas de entrada con nombres {0} y {1}, el módulo crea los nombres siguientes:
| Columnas | SingleSampleSet | PairedSamples | UnpairedSamples |
|---|---|---|---|
| Columna de salida P | P_ss({0}) | P_ps({0}, {1}) | P_us({0}, {1}) |
| Columna de salida RejectH0 | RejectH0_ss({0})" | RejectH0_ps({0}, {1}) | RejectH0_us({0}, {1}) |
Cómo se calculan las puntuaciones
Este módulo calcula y usa la desviación estándar de la muestra; por lo tanto, la ecuación usa (n-1) en el denominador.
Cálculo de puntuaciones para una prueba de ejemplo único
Dada una muestra única de puntuaciones, todas independientes entre sí, y una distribución normal, la puntuación se calcula de la siguiente manera:
Tome la entrada siguiente:
- Una columna única de valores desde el conjunto de datos
- Parámetro μ0 de hipótesis nula (H0)
- Puntuación de confianza especificada por α
Extraiga el número de muestras (n).
Calcule el promedio de los datos de la muestra.
Calcule la desviación estándar (s) de los datos de muestra.
Calcular t y grados de libertad (df):
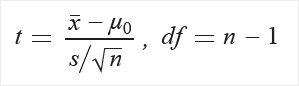
Extraiga la probabilidad P de la tabla de distribución T mediante t y df.
Cálculo de puntuaciones para una prueba t emparejada
Dado un conjunto de puntuaciones coincidente, con cada par independiente del otro, y una distribución normal en cada conjunto, la puntuación se calcula de la siguiente manera:
Tome la entrada siguiente:
- Dos columnas de valores del conjunto de datos
- Parámetro de hipótesis nula (H0) d0
- Puntuación de confianza especificada por α
Extraiga algún número de pares de ejemplo (n).
Calcule el promedio de las diferencias de los datos de las muestras:
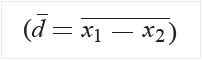
Calcule la desviación estándar de las diferencias (sd).
Calcular t y los grados de libertad (df):
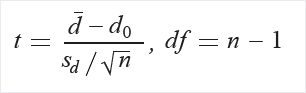
Extraiga la probabilidad (P) de la tabla de distribución (T) mediante t y df.
Cálculo de puntuaciones para una prueba t sin emparejar
Dadas dos muestras de puntuaciones independientes, con una distribución normal de valores en cada muestra, la puntuación se calcula de la siguiente manera:
Tome la entrada siguiente:
- Un conjunto de datos que contiene dos columnas de
doubles - Parámetro de hipótesis nula (H0) (d0)
- Puntuación de confianza especificada por α
- Un conjunto de datos que contiene dos columnas de
Extraiga una serie de muestras en cada grupo, n1 y n2.
Calcule los promedios de cada uno de los conjuntos de muestras.
Calcule la desviación estándar de cada grupo como s1 y s2.
Calcular t y grados de libertad (df):
Si así lo desea, puede cumplir el requisito de que la varianza entre los grupos sea aproximadamente la misma, del siguiente modo:
Calcule primero la desviación estándar agrupada:
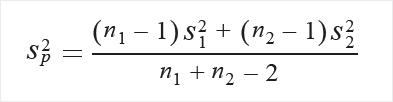
Si no hay ninguna suposición sobre la igualdad de las varianzas, realice el cálculo como sigue:
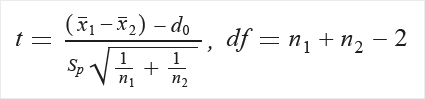
Extraiga P de la tabla de distribución (T) mediante t y df.
Computación de la hipótesis nula
La probabilidad de la hipótesis nula, designada como P, se calcula de la siguiente manera:
Si P < α, establezca la marca Reject en True.
Si P ≥ α, establezca la marca Reject en False.
Entradas esperadas
| Nombre | Tipo | Descripción |
|---|---|---|
| Dataset | Tabla de datos | Conjunto de datos de entrada |
Parámetros del módulo
| Nombre | Intervalo | Tipo | Valor predeterminado | Descripción |
|---|---|---|---|---|
| Tipo de hipótesis | Any | Hipótesis | Dos colas | Tipo de hipótesis nula de prueba t de Student |
| Μ hipotéticas nulas | Any | Float | 0,0 | En la prueba t de muestra única, la media hipotética nula de la muestra En la prueba t relacionada, la diferencia entre las muestras |
| Columnas de destino | Any | ColumnSelection | None | Patrón de selección de columnas de destino |
| Suponer varianzas iguales | Any | Boolean | True | Se supone que las varianzas de dos muestras son iguales Solo se aplica a las muestras no emparejadas. |
| Hipótesis nula μ1 | Any | Float | 0,0 | Media con hipótesis nula para la primera muestra |
| Α | [0.0;1.0] | Float | 0,95 | Factor de confianza (si P es inferior al factor de confianza, la hipótesis nula se rechaza) |
Salidas
| Nombre | Tipo | Descripción |
|---|---|---|
| P | Tabla de datos | Una puntuación de probabilidad que indica la confianza de la hipótesis nula |
| Rechazar H0 | Tabla de datos | Valor que indica si se debe rechazar la hipótesis nula |
Excepciones
| Excepción | Descripción |
|---|---|
| Error 0003 | Se produce una excepción si una o varias de las entradas son NULL o están vacías. |
| Error 0008 | Se produce una excepción si el parámetro no se encuentra en el intervalo. |
| Error 0017 | Se producen excepciones si una o más columnas especificadas tienen un tipo no compatible con el módulo actual. |
| Error 0020 | Se produce una excepción si el número de columnas de algunos de los conjuntos de datos que se pasan al módulo es demasiado pequeño. |
| Error 0021 | Se produce una excepción si el número de filas de algunos de los conjuntos de datos que se pasan al módulo es demasiado pequeño. |
| Error 0031 | Se produce una excepción si el número de columnas del conjunto de columnas es menor que el necesario. |
| Error 0032 | Se produce una excepción si el argumento no es un número. |
| Error 0033 | Se produce una excepción si el argumento es infinito. |
Para obtener una lista de errores específicos de los módulos de Studio (clásico), consulte Machine Learning códigos de error.
Para obtener una lista de excepciones de API, consulte Machine Learning códigos de error de la API REST.