Evaluación de la función de probabilidad
Importante
El soporte técnico de Machine Learning Studio (clásico) finalizará el 31 de agosto de 2024. Se recomienda realizar la transición a Azure Machine Learning antes de esa fecha.
A partir del 1 de diciembre de 2021 no se podrán crear recursos de Machine Learning Studio (clásico). Hasta el 31 de agosto de 2024, puede seguir usando los recursos de Machine Learning Studio (clásico) existentes.
- Consulte la información acerca de traslado de proyectos de aprendizaje automático de ML Studio (clásico) a Azure Machine Learning.
- Más información sobre Azure Machine Learning.
La documentación de ML Studio (clásico) se está retirando y es posible que no se actualice en el futuro.
Ajusta una función de distribución de probabilidad especificada a un conjunto de datos
Categoría: Funciones estadísticas
Nota
Se aplica a: solo Machine Learning Studio (clásico)
Hay módulos para arrastrar y colocar similares en el diseñador de Azure Machine Learning.
Información general sobre el módulo
En este artículo se describe cómo usar el módulo Evaluar función de probabilidad en Machine Learning Studio (clásico), para calcular medidas estadísticas que describen la distribución de una columna, como las distribuciones de Bernoulli, Pareto o Poisson.
Para usar este modelo, conecte un conjunto de datos que contenga al menos una columna de valores numéricos y elija una distribución de probabilidad para probar. El módulo devuelve una tabla de datos que contiene valores de la función de probabilidad especificada.
Puede calcular cualquiera de estos valores para la distribución de probabilidad elegida:
- función de distribución acumulativa (cdf)
- función de distribución acumulativa inversa (InverseCdf)
- función de densidad de probabilidad (Pdf)
¿Por qué es útil la distribución de probabilidad?
Al evaluar los datos con respecto a una distribución de probabilidad, se asignan valores de columna con un conjunto de valores con propiedades conocidas. Al saber si los datos corresponden a una de estas distribuciones conocidas, es posible que pueda deducir otras propiedades de los datos. En general, puede obtener mejores predicciones de un modelo si puede identificar la distribución que mejor se adapte a los datos.
La elección de una función de distribución de probabilidad depende de los datos y de las variables que se van a medir. Por ejemplo, algunas distribuciones están diseñadas para describir las probabilidades de valores discretos; otros están diseñados para su uso solo con variables numéricas continuas. Para algunas distribuciones, también debe conocer de antemano una media esperada, grados de libertad, etc. Para más información, consulte Distribuciones de probabilidad admitidas.
Configuración de la función Evaluate Probability
Todas las opciones cambian en función del tipo de distribución de probabilidad que quiera calcular. Si cambia el método de distribución de probabilidad, es posible que se restablezcan otras selecciones que haya realizado.
Por lo tanto, asegúrese de elegir primero la opción Distribución .
El conjunto de datos utilizado como entrada debe contener datos numéricos. Se omiten otros tipos de datos.
Para cada análisis, puede aplicar un único método de distribución de probabilidad. Para calcular una distribución de probabilidad diferente, agregue una instancia independiente del módulo para cada distribución que quiera probar.
Agregue el módulo Evaluate Probability Function (Evaluar función de probabilidad ) al experimento. Puede encontrar este módulo en la categoría Funciones estadísticas en Machine Learning Studio (clásico).
Conectar un conjunto de datos que contiene al menos una columna de números.
Use la opción Distribución para seleccionar el tipo de distribución de probabilidad que desea calcular. Consulte Distribuciones de probabilidad admitidas para obtener una lista de opciones y sus argumentos necesarios.
Establezca los parámetros necesarios para la distribución.
Elija una de las tres estadísticas que se van a crear: la función de distribución acumulativa (cdf), la función de distribución acumulativa inversa (InverseCdf) o la función de densidad de probabilidad (pdf).
Consulte la sección Notas técnicas para ver las definiciones.
Use el selector de columnas para elegir las columnas sobre las que calcular la distribución de probabilidad seleccionada.
Todas las columnas que seleccione deben tener un tipo de datos numérico.
El intervalo de datos de la columna también debe ser válido, dada la función de probabilidad seleccionada. De lo contrario, puede producirse un error o un resultado NaN.
En el caso de las columnas dispersas, no se procesará ningún valor que se corresponda con ceros de fondo.
Use la opción Modo de resultado para especificar cómo generar los resultados. Puede reemplazar los valores de columna con los valores de distribución de probabilidad, anexar los nuevos valores al conjunto de datos o devolver únicamente los valores de distribución de probabilidad.
Ejecute el experimento o haga clic con el botón derecho en el módulo Evaluar función de probabilidad y haga clic en Ejecutar seleccionado.
Results
La tabla siguiente contiene un ejemplo de resultados, mediante la opción Append , en una sola columna de temperatura del conjunto de datos de ejemplo Forest Fires .
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp | FFisher.cdf(temp |
|---|---|---|---|---|
| 8,2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11.4 | 1 | 1 | 0.993147 | 0.001502 |
Los encabezados de las columnas generadas contienen la distribución de probabilidad que se usó.
Si no está seguro de qué distribución de probabilidad es probable que se adapte a los datos, puede crear un gráfico rápido de distribución acumulativa y densidad de probabilidad para cualquier columna numérica.
- Haga clic con el botón derecho en el conjunto de datos o la salida del módulo y seleccione Visualizar.
- Seleccione la columna de interés y, en el panel Histograma , seleccione distribución acumulativa o densidad de probabilidad.
- Un gráfico de la distribución, como el siguiente, se superpone en el histograma que representa los datos.
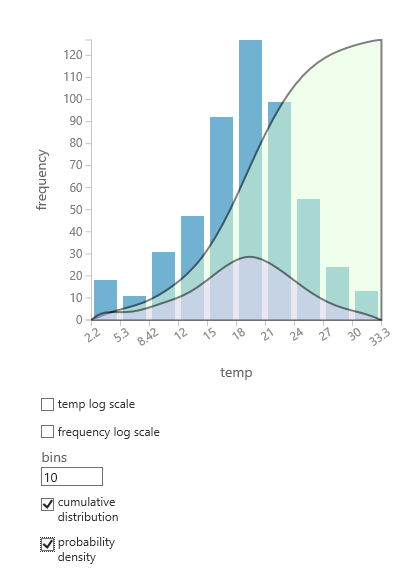
Distribuciones de probabilidad admitidas
El módulo Evaluate Probability Function admite las siguientes distribuciones:
Bernoulli
La distribución de Bernoulli es una distribución sobre valores binarios: en otras palabras, modela la distribución esperada cuando solo son posibles dos valores.
Para calcular, seleccione Bernoulli y establezca las siguientes opciones:
- Probabilidad de éxito
El parámetro p especifica la probabilidad de que se genere un 1. Escriba un número (float) entre 0,0 y 1,0 que especifique la probabilidad de éxito. El valor predeterminado es .5.
Beta
La distribución beta es una distribución univariante continua.
Para calcular, seleccione Beta y establezca las siguientes opciones:
Forma
Escriba un valor para cambiar la forma de la distribución.Un parámetro de forma es cualquier parámetro de una distribución de probabilidad que no define su ubicación o escala. Por lo tanto, al especificar un valor para la forma, el parámetro cambia la forma de la distribución, en lugar de moverla, expandirla o contraerla.
El valor debe ser un número (
double). El valor predeterminado es 1.0.Escala
Escriba un número para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Límite superior
Escriba un número (double) que represente el límite superior de la distribución. El valor predeterminado es 1.0.Límite inferior
Escriba un número (double) que represente el límite superior de la distribución. El valor predeterminado es 0,0.
Binomial
La distribución binomial es una distribución univariante discreta. La distribución binomial se usa para modelar el número de éxitos en una muestra. Durante el muestreo se utiliza el reemplazo. En el caso del muestreo sin reemplazo, use la distribución hipergeométrica.
Para calcular, seleccione Binomial y establezca las siguientes opciones:
Probabilidad de éxito
Escriba un número (float) entre 0,0 y 1,0 que indique la probabilidad de éxito. El valor predeterminado es .5.Número de pruebas
Especifique el número de pruebas.Use un
integer, con un valor mínimo de 1. El valor predeterminado es 3.
Cauchy
La distribución de Cauchy es una distribución de probabilidad continua simétrica.
Para calcular, seleccione Cauchy y establezca las siguientes opciones:
Ubicación
Escriba un número (double) que represente la ubicación del0º elemento.Si especifica un valor para el parámetro Ubicación, puede cambiar la distribución de probabilidad hacia arriba o hacia abajo en una escala numérica.
El valor predeterminado es 0,0.
ChiSquare
La distribución chi cuadrado es una suma de los cuadrados de k variables independientes, estándar, normales y aleatorias.
Para calcular, seleccione ChiSquare y establezca las siguientes opciones:
- Número de grados de libertad Escriba un número (
double) para especificar los grados de libertad. El valor predeterminado es 1.0.
ChiSquareRightTailed
Esta opción proporciona una distribución chi cuadrado de cola derecha.
Para calcular, seleccione ChiSquareRightTailed y establezca las siguientes opciones:
- Número de grados de libertad
Escriba un número (double) para especificar los grados de libertad. El valor predeterminado es 1.0.
Exponencial
La distribución exponencial es una distribución sobre los números reales parametrizados por un parámetro no negativo.
Para calcular, seleccione Exponencial y establezca las siguientes opciones:
- Lambda
Escriba un número (double) para usarlo como parámetro lambda. El valor predeterminado es 1.0.
FFisher
Genera la probabilidad de la estadística fisher para una muestra, también conocida como distribución de Fisher F. Esta distribución es de dos colas.
Para calcular, seleccione FFisher y establezca las siguientes opciones:
Grados de libertad del numerador
Escriba un número (double) para especificar los grados de libertad que se usan en el numerador. El valor predeterminado es 3.0.Grados de libertad del denominador
Escriba un número (double) para especificar los grados de libertad que se usan en el denominador. El valor predeterminado es 6.0.
FFisherRightTailed
Crea una distribución de Fisher de cola derecha. La distribución de Fisher también se conoce como la distribución F de Fisher, la distribución de Snedecor o la distribución de Fisher-Snedecor. Esta forma especial de la distribución es de cola derecha.
Para calcular, seleccione FFisherRightTailed y establezca las siguientes opciones:
Grados de libertad del numerador
Escriba un número (double) para especificar los grados de libertad que se usan en el numerador. El valor predeterminado es 3.0.Grados de libertad del denominador
Escriba un número (double) para especificar los grados de libertad que se usan en el denominador. El valor predeterminado es 6.0.
Gamma
La distribución gamma es una familia de distribuciones de probabilidad continuas con dos parámetros. Por ejemplo, chi cuadrado es un caso especial de la distribución gamma.
Para calcular, seleccione Gamma y establezca las siguientes opciones:
Escala
Escriba un valor para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Ubicación
Escriba un número (double) que represente la ubicación del0º elemento.Si especifica un valor para el parámetro Ubicación, puede cambiar la distribución de probabilidad hacia arriba o hacia abajo en una escala numérica.
El valor predeterminado es 0,0.
GeneralizedExtremeValues
Crea una distribución desarrollada para controlar valores extremos. La distribución de valores extremos generalizada (GEV) es, en realidad, un grupo de distribuciones de probabilidad continua que combina las distribuciones de Gumbel, Fréchet y Weibull (también conocidas como distribuciones de valor extremo de tipo I, II y III).
Para obtener más información sobre la teoría del valor extremo, consulte este artículo en Wikipedia: Teorema Fisher-Tippet-Gnedenko.
Para calcular, seleccione GeneralizedE extremeValues y establezca las siguientes opciones:
Forma
Escriba un valor para cambiar la forma de la distribución.Un parámetro de forma es cualquier parámetro de una distribución de probabilidad que no define su ubicación o escala. Por lo tanto, al especificar un valor para la forma, el parámetro cambia la forma de la distribución, en lugar de moverla, expandirla o contraerla.
El valor debe ser un número (
double). El valor predeterminado es 1.0.Escala
Escriba un valor para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Ubicación
Escriba un número (double) que represente la ubicación del0º elemento.Si escribe un valor para el parámetro Ubicación, puede cambiar la distribución de probabilidad hacia arriba o hacia abajo en una escala numérica.
El valor predeterminado es 0,0.
Geométrico
La distribución geométrica es una distribución sobre enteros positivos parametrizados por un número real positivo.
Para calcular, seleccione Geométrico y establezca las siguientes opciones:
- Probabilidad de éxito
Escriba un número (float) entre 0,0 y 1,0 que indique la probabilidad de éxito. El valor predeterminado es .5.
Nota
Esta implementación de la distribución geométrica no genera ceros.
GumbelMax
La distribución de Gumbel es una de las diversas distribuciones de valores extremos. La opción GumbelMax implementa la distribución de valores extremos máximos de tipo 1.
Para calcular, seleccione GumbelMax y establezca las siguientes opciones:
Escala
Escriba un valor para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Ubicación
Escriba un número (double) que represente la ubicación del0º elemento.Si escribe un valor para el parámetro Ubicación, puede cambiar la distribución de probabilidad hacia arriba o hacia abajo en una escala numérica.
El valor predeterminado es 0,0.
GumbelMin
La distribución de Gumbel es una de las diversas distribuciones de valores extremos. La distribución de Gumbel también se conoce como la distribución de valores extremos mínimos (SEV) o distribución de valores extremos mínimos (tipo I). La opción GumbelMin implementa la distribución de tipo 1 de valor extremo mínimo.
Para calcular, seleccione GumbelMin y debe establecer las siguientes opciones:
Escala
Escriba un valor para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Ubicación
Escriba un número (double) que represente la ubicación del0º elemento.Si escribe un valor para el parámetro Ubicación, puede cambiar la distribución de probabilidad hacia arriba o hacia abajo en una escala numérica.
El valor predeterminado es 0,0.
Hipergeométrica
La distribución hipergeométrica es una distribución de probabilidad discreta que describe el número de éxitos en una secuencia de n se extrae de una población finita sin reemplazo, al igual que la distribución binomial describe el número de éxitos para los sorteos con reemplazo.
Para calcular, seleccione Hypergeometric y establezca las siguientes opciones:
Número de muestras
Escriba un entero que indique el número de muestras que se van a usar. El valor predeterminado es 9.Número de aciertos
Escriba un entero que defina el valor para el acierto. El valor predeterminado es 24.Tamaño de la población
Especifique el tamaño de población que se usará al estimar la distribución hipergeométrica.
Laplace
La distribución de Laplace es una distribución sobre los números reales, parametrizados por una media y por un parámetro de escala.
Para calcular, seleccione Distribución de Laplace y establezca las siguientes opciones:
Escala
Escriba un valor para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Ubicación
Escriba un número (double) que represente la ubicación del0º elemento.Si escribe un valor para el parámetro Ubicación, puede cambiar la distribución de probabilidad hacia arriba o hacia abajo en una escala numérica.
El valor predeterminado es 0,0.
Logística
La distribución logística es similar a la distribución normal, pero no tiene límite en el lado izquierdo de la distribución. La distribución logística se utiliza en los modelos de red neuronal y regresión logística, así como para el modelado de datos de las ciencias biológicas.
Para calcular, seleccione Logística y establezca las siguientes opciones:
Escala
Escriba un valor para utilizarlo en el escalado de la distribución.Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.
El valor predeterminado es 1,0. Los valores deben ser números positivos.
Promedio
Escriba un número (double) que indique el valor medio estimado de la distribución. El valor predeterminado es 0,0.
Logarítmico-normal
La distribución logarítmico-normal es una distribución univariante continua.
Para calcular, seleccione Lognormal y establezca las siguientes opciones:
Promedio
Escriba un número (double) que indique el valor medio estimado de la distribución. El valor predeterminado es 0,0.Desviación estándar
Escriba un número positivo (double) que indique la desviación estándar estimada de la distribución. El valor predeterminado es 1.0.
NegativeBinomial
La distribución binomial negativa es una distribución sobre los números naturales con dos parámetros (r, p). En el caso especial que r es un entero, puede interpretar la distribución como el número de colas antes de lacabeza r cuando la probabilidad de la cabeza es p.
Para calcular, seleccione NegativeBinomial y establezca las siguientes opciones:
Probabilidad de éxito
Escriba un número (float) entre 0,0 y 1,0 que indique la probabilidad de éxito. El valor predeterminado es .5.Número de aciertos
Escriba un entero que especifique el valor para el acierto. El valor predeterminado es 24.
Normal
La distribución normal también se conoce como distribución gaussiana.
Para calcular, seleccione Normal y establezca las siguientes opciones:
Promedio
Escriba un número (double) que indique el valor medio estimado de la distribución. El valor predeterminado es 0,0.Desviación estándar
Escriba un número positivo (double) que indique la desviación estándar estimada de la distribución. El valor predeterminado es 1.0.
Pareto
La distribución de Pareto es una distribución de probabilidad de ley potencial que coincide con fenómenos observables sociales, científicos, geofísicos, actuarios y de muchos otros tipos.
Para calcular, seleccione Pareto y establezca las siguientes opciones:
Forma
Escriba un valor (opcional) para cambiar la forma de la distribución.Un parámetro de forma es cualquier parámetro de una distribución de probabilidad que no define su ubicación o escala. Por lo tanto, al especificar un valor para la forma, el parámetro cambia la forma de la distribución, en lugar de moverla, expandirla o contraerla.
El valor debe ser un número (
double). El valor predeterminado es 1.0.Escala
Escriba un valor (opcional) para cambiar la escala de la distribución. Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.El valor debe ser un número (
double). El valor predeterminado es 1.0.
Poisson
En esta implementación, el método de Knuth sirve para generar variables aleatorias distribuidas de Poisson. Para obtener más información sobre la distribución de Poisson, consulte Regresión de Poisson.
Para calcular, seleccione Poisson y establezca las siguientes opciones:
- Promedio
Escriba un número (double) que indique el valor medio estimado de la distribución. El valor predeterminado es 0,0.
Rayleigh
La distribución de Rayleigh es una distribución de probabilidad continua. Un ejemplo de cómo se produce sería el siguiente: la velocidad del viento tendrá una distribución de Rayleigh si los componentes del vector bidimensional de velocidad del viento no están correlacionados y se distribuyen normalmente con una varianza igual.
Para calcular, seleccione Rayleigh y establezca las siguientes opciones:
- Límite inferior
Escriba un número (double) que represente el límite superior de la distribución. El valor predeterminado es 0,0.
StandardNormal
Esta opción proporciona la distribución normal estándar, sin otros parámetros.
Para calcular, seleccione StandardNormal y seleccione las columnas.
TStudent
Esta opción implementa la distribución t de Student univariante.
Para calcular, seleccione TStudent y establezca las siguientes opciones:
- Número de grados de libertad
Escriba un número (double) para especificar los grados de libertad. El valor predeterminado es 1.0.
TStudentRightTailed
Implementa la distribución t de Student univariante mediante el uso de una cola derecha.
Para calcular, seleccione TStudentRightTailed y establezca las siguientes opciones:
- Número de grados de libertad
Escriba un número (double) para especificar los grados de libertad. El valor predeterminado es 1.0.
TStudentTwoTailed
Implementa una distribución t de Student de dos colas.
Para calcular, seleccione TStudentTwoTailed y establezca las siguientes opciones:
- Número de grados de libertad
Escriba un número (double) para especificar los grados de libertad. El valor predeterminado es 1.0.
Uniforme
La distribución uniforme también se conoce como la distribución rectangular.
Para calcular, seleccione Uniforme y establezca las siguientes opciones:
Límite inferior
Escriba un número (double) que represente el límite inferior de la distribución. El valor predeterminado es 0,0.Límite superior
Escriba un número (double) que represente el límite superior de la distribución. El valor predeterminado es 1.0.
Weibull
La distribución de Weibull se usa ampliamente en la ingeniería de fiabilidad. Puede usar su parámetro Shape para modelar muchas otras distribuciones.
Para calcular, seleccione Weibull y establezca las siguientes opciones:
Forma
Escriba un valor (opcional) para cambiar la forma de la distribución.Un parámetro de forma es cualquier parámetro de una distribución de probabilidad que no define su ubicación o escala. Por lo tanto, al especificar un valor para la forma, el parámetro cambia la forma de la distribución, en lugar de moverla, expandirla o contraerla.
El valor debe ser un número (
double). El valor predeterminado es 1.0.Escala
Escriba un valor (opcional) para cambiar la escala de la distribución. Al aplicar un valor de escala a la distribución, puede contraerla o expandirla.El valor debe ser un número (
double). El valor predeterminado es 1.0.
Notas técnicas
Esta sección contiene detalles de implementación, sugerencias y respuestas a las preguntas más frecuentes.
Detalles de la implementación
Este módulo es compatible con todas las distribuciones que se proporcionan en la biblioteca numérica de MATH.NET de código abierto. Para obtener más información, consulte la documentación de la biblioteca Math.Net.Numerics.Distribution .
Las distribuciones de cola derecha y de dos colas aparecen como distribuciones independientes, no como versiones con parámetros de las distribuciones base. El comportamiento actual es mantener la compatibilidad con Excel.
Definiciones
Este módulo admite el cálculo de cualquiera de estos valores para la distribución especificada:
cdf o la función de distribución acumulativa
Devuelve la probabilidad de un evento compuesto, definido como la suma de los casos cuando la variable aleatoria toma un valor menor que algún valor específico x.
En otras palabras, responde a la pregunta: "¿Cómo son las muestras comunes que son menores o iguales que este valor?"
Esta función se puede usar con variables numéricas continuas y discretas.
InverseCdf o la función de distribución acumulativa inversa
Devuelve el valor asociado a un valor de probabilidad acumulado específico (cdf).
En otras palabras, responde a la pregunta: "¿Cuál es el valor de x en el que la función cdf devuelve la probabilidad acumulativa y?"
pdf, o la función de densidad de probabilidad
Describe la probabilidad relativa de que una variable aleatoria sea un valor específico.
En otras palabras, responde a la pregunta: "¿Cómo son las muestras comunes exactamente este valor?"
Entradas esperadas
| Nombre | Tipo | Descripción |
|---|---|---|
| Dataset | Tabla de datos | Conjunto de datos de entrada |
Parámetros del módulo
| Nombre | Intervalo | Tipo | Valor predeterminado | Descripción |
|---|---|---|---|---|
| Distribución | Any | ProbabilityDistribution | StandardNormal | Seleccione el tipo de distribución de probabilidad que se va a generar. |
| Método | Any | ProbabilityDistributionMethod | Cdf | Seleccione el método que se va a usar para calcular la distribución de probabilidad seleccionada. Las opciones son la función de distribución acumulativa (cdf), la función de distribución acumulativa inversa (InverseCdf) y la función de densidad de probabilidad o función bruta (pdf). |
| Método de distribución binomial negativa | Any | ProbabilityDistributionMethodForNegativeBinomial | Cdf | Si selecciona la distribución binomial negativa, especifique el método utilizado para evaluar la distribución. |
| Probabilidad de éxito | [0.0;1.0] | Float | 0.5 | Escriba un valor que se usará como probabilidad de éxito. |
| Forma | Any | Float | 1,0 | Escriba un valor que modifique la forma de la distribución. |
| Escala | >=0.0 | Float | 1,0 | Escriba un valor que cambie la escala de la distribución para expandir o reducir su tamaño. |
| Número de pruebas | >=1 | Entero | 3 | Especifique el número de pruebas. |
| Límite inferior | Any | Float | 0,0 | Escriba un número que usará como el límite inferior de la distribución |
| Límite superior | Any | Float | 1,0 | Escriba un número que usará como el límite superior de la distribución |
| Ubicación | Any | Float | 0,0 | Escriba la ubicación del elemento cero en la distribución. |
| Número de grados de libertad | Any | Float | 1,0 | Especifique el número de grados de libertad. |
| Grados de libertad del numerador | Any | Float | 3.0 | Especifique el número de grados de libertad del numerador. |
| Grados de libertad del denominador | Any | Float | 6.0 | Especifique el número de grados de libertad del denominador. |
| Lambda | >=0.0 | Float | 1,0 | Especifique un valor para el parámetro lambda. |
| Número de ejemplos | Any | Entero | 9 | Especifique el número de muestras. |
| Número de aciertos | Any | Entero | 24 | Escriba un valor que se usará como número de aciertos. |
| Tamaño de la población | Any | Entero | 52 | Especifique el tamaño de la población. |
| Media | Any | Float | 0,0 | Escriba el valor medio estimado. |
| Desviación estándar | >=0.0 | Float | 1,0 | Escriba la desviación estándar estimada. |
| Conjunto de columnas | Any | ColumnSelection | Elija las columnas en las que se va a calcular la distribución de probabilidad. | |
| Modo de resultados | Any | OutputTo | ResultOnly | Especifique cómo se van a guardar los resultados en el conjunto de datos de salida. Las opciones son agregar nuevas columnas, sustituir las columnas existentes o dar salida solo a los resultados. |
Output
| Nombre | Tipo | Descripción |
|---|---|---|
| Conjunto de datos de resultados | Tabla de datos | Conjunto de datos de salida |
Excepción
Para obtener una lista completa de los mensajes de error, consulte Códigos de error del módulo.
| Excepción | Descripción |
|---|---|
| Error 0017 | Se producen excepciones si una o más columnas especificadas tienen un tipo no compatible con el módulo actual. |
Para obtener una lista de errores específicos de los módulos de Studio (clásico), consulte códigos de error Machine Learning.
Para obtener una lista de excepciones de API, consulte Machine Learning códigos de error de la API REST.