Anhang: Matrixtransformationen
Dieses Thema bietet eine mathematische Übersicht über Matrixtransformationen für 2D-Grafiken. Sie müssen jedoch keine Matrixmathematik kennen, um Transformationen in Direct2D verwenden zu können. Lesen Sie dieses Thema, wenn Sie sich für die Mathematik interessieren. Andernfalls können Sie dieses Thema überspringen.
Einführung in Matrizen
Eine Matrix ist ein rechteckiges Array reelle Zahlen. Die Reihenfolge der Matrix ist die Anzahl der Zeilen und Spalten. Wenn die Matrix beispielsweise 3 Zeilen und 2 Spalten enthält, beträgt die Reihenfolge 3 × 2. Matrizen werden in der Regel mit den Matrixelementen angezeigt, die in eckige Klammern eingeschlossen sind:
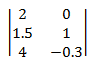
Notation: Eine Matrix wird durch einen Großbuchstaben gekennzeichnet. Elemente werden durch Kleinbuchstaben gekennzeichnet. Tiefgestellte geben die Zeilen- und Spaltennummer eines Elements an. Beispielsweise ist einij das Element in der i'ten Zeile und der j'ten Spalte der Matrix A.
Das folgende Diagramm zeigt eine i × j-Matrix mit den einzelnen Elementen in jeder Zelle der Matrix.

Matrixvorgänge
In diesem Abschnitt werden die grundlegenden Vorgänge beschrieben, die für Matrizen definiert sind.
Addition. Die Summe A + B von zwei Matrizen wird durch Hinzufügen der entsprechenden Elemente von A und B abgerufen:
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
Skalare Multiplikation. Dieser Vorgang multipliziert eine Matrix mit einer reellen Zahl. Bei einer reellen Zahl k wird das Skalarprodukt kA durch Multiplikation jedes Elements von A mit k erhalten.
- kA = k\[ a*ij* \] = \[ k × a*ij* \]
Matrixmultiplikation. Bei zwei Matrizen A und B mit der Reihenfolge (m × n) und (n × p) ist das Produkt C = A × B eine Matrix mit der Reihenfolge (m × p), die wie folgt definiert ist:
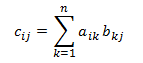
oder gleichwertig:
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*
Gehen Sie also wie folgt vor, um jedes Element cij zu berechnen:
- Nehmen Sie die erste Zeile von A und die j'th-Spalte von B.
- Multiplizieren Sie jedes Elementpaar in der Zeile und Spalte: den ersten Zeileneintrag mit dem ersten Spalteneintrag, den zweiten Zeileneintrag mit dem zweiten Spalteneintrag usw.
- Summieren Sie das Ergebnis.
Hier sehen Sie ein Beispiel für die Multiplikation einer Matrix (2 × 2) mit einer Matrix (2 × 3).
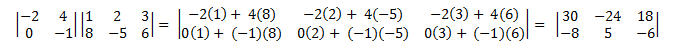
Die Matrixmultiplikation ist nicht kommutativ. Das heißt, A × B ≠ B × A. Außerdem ergibt sich aus der Definition, dass nicht jedes Paar von Matrizen multipliziert werden kann. Die Anzahl der Spalten in der linken Matrix muss der Anzahl der Zeilen in der rechten Matrix entsprechen. Andernfalls ist der ×-Operator nicht definiert.
Identifizieren Sie die Matrix. Eine Identitätsmatrix mit der Bezeichnung I ist eine quadratische Matrix, die wie folgt definiert ist:
- I*ij* = 1, wenn *i* = *j* oder andernfalls 0.
Anders ausgedrückt: Eine Identitätsmatrix enthält 1 für jedes Element, wobei die Zeilennummer der Spaltennummer entspricht, und null für alle anderen Elemente. Hier sehen Sie beispielsweise die Identitätsmatrix 3 × 3.
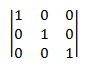
Die folgenden Gleichheiten gelten für jede Matrix M.
- M x I = M I x M = M
Affine Transformationen
Eine affine Transformation ist eine mathematische Operation, die einen Koordinatenraum einem anderen zuordnet. Anders ausgedrückt: Es ordnet einen Satz von Punkten einem anderen Satz von Punkten zu. Affine Transformationen verfügen über einige Features, die sie in Computergrafiken nützlich machen.
- Affine Transformationen behalten die Kollinearität bei. Wenn drei oder mehr Punkte auf eine Linie fallen, bilden sie nach der Transformation immer noch eine Linie. Gerade Linien bleiben gerade.
- Die Zusammensetzung zweier affiner Transformationen ist eine affine Transformation.
Affine Transformationen für 2D-Leerzeichen haben die folgende Form.
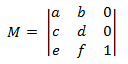
Wenn Sie die zuvor angegebene Definition der Matrixmultiplikation anwenden, können Sie zeigen, dass das Produkt zweier affiner Transformationen eine weitere affine Transformation ist. Um einen 2D-Punkt mithilfe einer affinen Transformation zu transformieren, wird der Punkt als Matrix von 1 × 3 dargestellt.
- P = \| x y 1 \|
Die ersten beiden Elemente enthalten die x- und y-Koordinaten des Punkts. Die 1 wird im dritten Element platziert, damit die Mathematik ordnungsgemäß funktioniert. Um die Transformation anzuwenden, multiplizieren Sie die beiden Matrizen wie folgt.
- P' = P × M
Dies wird auf Folgendes erweitert.
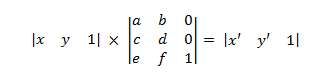
where
- x' = ax + cy + e y' = bx + dy + f
Um den transformierten Punkt abzurufen, nehmen Sie die ersten beiden Elemente der Matrix P'.
- p = (x', y') = (ax + cy + e, bx + dy + f)
Hinweis
Eine 1 × n Matrix wird als Zeilenvektor bezeichnet. Direct2D und Direct3D verwenden beide Zeilenvektoren, um Punkte im 2D- oder 3D-Raum darzustellen. Sie können ein gleichwertiges Ergebnis erhalten, indem Sie einen Spaltenvektor (n × 1) verwenden und die Transformationsmatrix transponieren. Die meisten Grafiktexte verwenden das Spaltenvektorformular. In diesem Thema wird das Zeilenvektorformular für die Konsistenz mit Direct2D und Direct3D vorgestellt.
In den nächsten Abschnitten werden die grundlegenden Transformationen abgeleitet.
Übersetzungstransformation
Die Übersetzungstransformationsmatrix hat die folgende Form.
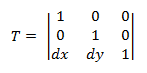
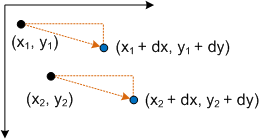
Das Einfügen eines Punkts P in diese Gleichung ergibt Folgendes:
- P' = (*x* + *dx*, *y* + *dy*)
Dies entspricht dem Punkt (x, y), der von dx in der X-Achse und dy in der Y-Achse übersetzt wird.
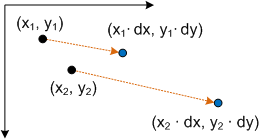
Skalierungstransformation
Die Skalierungstransformationsmatrix hat die folgende Form.
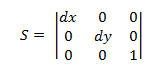
Das Einfügen eines Punkts P in diese Gleichung ergibt Folgendes:
- P' = (*x* ∙ *dx*, *y* ∙ *dy*)
die dem punkt (x,y) entspricht, der nach dx und dy skaliert ist.
Drehung um den Ursprung
Die Matrix, um einen Punkt um den Ursprung zu rotieren, hat die folgende Form.
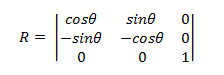
Der transformierte Punkt ist:
- P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)
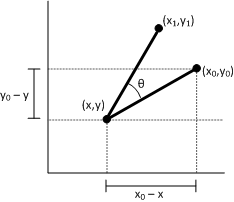
Beweis. Um zu zeigen, dass P' eine Drehung darstellt, sehen Sie sich das folgende Diagramm an.
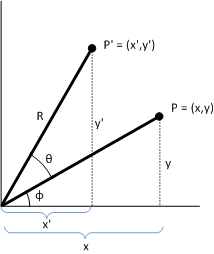
Gegeben:
-
P = (x,y)
-
Der ursprüngliche zu transformierenden Punkt.
-
Φ
-
Der Von der Linie (0,0) zu P gebildete Winkel.
-
Θ
-
Der Winkel, um den der Ursprung gedreht werden soll (x,y).
-
P' = (x',y')
-
Der transformierte Punkt.
-
R
-
Die Länge der Linie (0,0) zu P. Auch der Radius des Kreises der Drehung.
Hinweis
Dieses Diagramm verwendet das Standardkoordinatensystem, das in der Geometrie verwendet wird, wobei die positive y-Achse nach oben zeigt. Direct2D verwendet das Windows-Koordinatensystem, bei dem die positive y-Achse nach unten zeigt.
Der Winkel zwischen der x-Achse und der Linie (0,0) zu P' ist Φ + Θ. Die folgenden Identitäten enthalten:
- x = R cosΦ y = R sinΦ x' = R cos(Φ + Θ) y' = R sin(Φ+ Θ)
Lösen Sie nun für x' und y' in Bezug auf Θ. Anhand der trigonometrischen Additionsformeln:
- x' = R(cosΦcosΘ – sinΦsinΘ) = RcosΦcosΘ – RsinΦsinΘ y' = R(sinΦcosΘ + cosΦsinΘ) = RsinΦcosΘ + RcosΦsinΘ
Ersetzen, erhalten wir Folgendes:
- x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ
die dem transformierten Punkt P' entspricht, der zuvor gezeigt wurde.
Drehung um einen beliebigen Punkt
Um um einen anderen Punkt (x,y) als den Ursprung zu rotieren, wird die folgende Matrix verwendet.
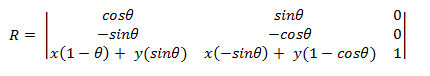
Sie können diese Matrix ableiten, indem Sie den Punkt (x,y) als Ursprung nehmen.
Lassen Sie (x1, y1) den Punkt sein, der sich aus der Drehung des Punkts (x0, y0) um den Punkt (x,y) ergibt. Wir können x1 wie folgt ableiten.
- x1 = (x0 – x)cosΘ – (y0 – y)sinΘ + x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]
Schließen Sie diese Gleichung nun wieder in die Transformationsmatrix ein, indem Sie die Formel x1 = ax0 + cy0 + e von früher verwenden. Verwenden Sie das gleiche Verfahren, um y1 abzuleiten.
Schiefe Transformation
Die Schiefetransformation wird durch vier Parameter definiert:
- Θ: Die Menge, die entlang der x-Achse als Winkel von der y-Achse gemessen werden soll.
- Φ: Die Menge, die entlang der y-Achse gedreht werden soll, gemessen als Winkel von der x-Achse.
- (px, py): Die x- und y-Koordinaten des Punkts, an dem die Abweichung ausgeführt wird.
Die Verzerrungstransformation verwendet die folgende Matrix.
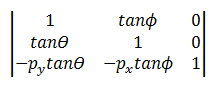
Der transformierte Punkt ist:
- P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΦ) – *py*tanΦ
oder gleichwertig:
- P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΦ)
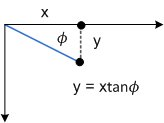
Um zu sehen, wie diese Transformation funktioniert, betrachten Sie jede Komponente einzeln. Der Parameter Θ verschiebt jeden Punkt in x-Richtung um eine Menge, die tanΘ entspricht. Das folgende Diagramm zeigt die Beziehung zwischen Θ und der x-Achsen-Neigung.
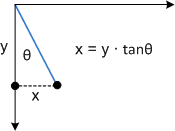
Hier ist die gleiche Schiefe, die auf ein Rechteck angewendet wird:
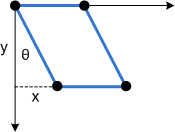
Der Parameter Φ hat den gleichen Effekt, aber entlang der y-Achse:
Das nächste Diagramm zeigt eine Y-Achsenschiefe, die auf ein Rechteck angewendet wird.
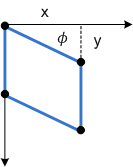
Schließlich verschieben die Parameter px und py den Mittelpunkt für die Neigung entlang der x- und y-Achse.
Darstellen von Transformationen in Direct2D
Alle Direct2D-Transformationen sind affine Transformationen. Direct2D unterstützt keine nicht affinen Transformationen. Transformationen werden durch die D2D1_MATRIX_3X2_F-Struktur dargestellt. Diese Struktur definiert eine Matrix mit 3 × 2. Da die dritte Spalte einer affinen Transformation immer gleich ist ([0, 0, 1]), und da Direct2D keine nicht affinen Transformationen unterstützt, ist es nicht erforderlich, die gesamte 3 ×3-Matrix anzugeben. Intern verwendet Direct2D 3 × 3 Matrizen, um die Transformationen zu berechnen.
Die Member der D2D1_MATRIX_3X2_F werden entsprechend ihrer Indexposition benannt: Das _11-Element ist Element (1,1), das _12-Element ist element (1,2) usw. Obwohl Sie die Strukturmember direkt initialisieren können, wird empfohlen, die D2D1::Matrix3x2F-Klasse zu verwenden. Diese Klasse erbt D2D1_MATRIX_3X2_F und stellt Hilfsmethoden zum Erstellen einer der grundlegenden affinen Transformationen bereit. Die -Klasse definiert auch operator*() für das Komponieren von zwei oder mehr Transformationen, wie unter Anwenden von Transformationen in Direct2D beschrieben.
Nächste