Nicht affine Transformationen
Erstellen von Perspektiv- und Tippeffekten mit der dritten Spalte der Transformationsmatrix
Übersetzung, Skalierung, Drehung und Skewing werden alle als affine Transformationen klassifiziert. Affine Transformationen erhalten parallele Linien. Wenn zwei Zeilen vor der Transformation parallel sind, werden sie nach der Transformation parallel Standard. Rechtecke werden immer in Parallelogramme transformiert.
SkiaSharp ist jedoch auch in der Lage, nicht affine Transformationen zu verwenden, die die Möglichkeit haben, ein Rechteck in ein konvexes Quadrilateral zu transformieren:

Ein konvexes Viereck ist eine vierseitige Figur mit Innenwinkeln immer weniger als 180 Grad und Seiten, die sich nicht gegenseitig kreuzen.
Nicht affine Transformationen ergeben sich, wenn die dritte Zeile der Transformationsmatrix auf andere Werte als 0, 0 und 1 festgelegt ist. Die vollständige SKMatrix Multiplikation lautet:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
Die resultierenden Transformationsformeln sind:
x' = ScaleX·x + SkewX·y + TransX
y' = SkewY·x + ScaleY·y + TransY
z' = Persp0·x + Persp1·y + Persp2
Die Grundregel der Verwendung einer 3:3-Matrix für zweidimensionale Transformationen besteht darin, dass alles auf der Ebene, auf der Z gleich 1 ist, wieder Standard. Sofern Persp0 nicht 0 und Persp1 Persp2 gleich 1 sind, hat die Transformation die Z-Koordinaten aus dieser Ebene verschoben.
Um dies in einer zweidimensionalen Transformation wiederherzustellen, müssen die Koordinaten wieder auf diese Ebene verschoben werden. Ein weiterer Schritt ist erforderlich. Die Werte "x", "y" und "z" müssen durch z dividiert werden:
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
Diese sind als homogene Koordinaten bekannt und wurden von Mathematiker August Ferdinand Möbius entwickelt, viel besser bekannt für seine topologische Ungerade, den Möbius Strip.
Wenn z' 0 ist, führt die Division zu unendlichen Koordinaten. Tatsächlich war eine der Motivationen von Möbius für die Entwicklung homogener Koordinaten die Fähigkeit, unendliche Werte mit endlichen Zahlen darzustellen.
Beim Anzeigen von Grafiken möchten Sie jedoch vermeiden, dass etwas mit Koordinaten gerendert wird, die sich in unendliche Werte umwandeln. Diese Koordinaten werden nicht gerendert. Alles in der Nähe dieser Koordinaten wird sehr groß und wahrscheinlich nicht visuell kohärent sein.
In dieser Gleichung möchten Sie nicht, dass der Wert von z null wird:
z' = Persp0·x + Persp1·y + Persp2
Folglich haben diese Werte einige praktische Einschränkungen:
Die Persp2 Zelle kann entweder null oder nicht null sein. Wenn Persp2 null ist, ist z' für den Punkt (0, 0) null, und das ist in der Regel nicht wünschenswert, da dieser Punkt in zweidimensionalen Grafiken sehr häufig ist. Wenn Persp2 nicht gleich 0, gibt es keinen Verlust der Allgemeinheit, wenn Persp2 bei 1 festgelegt ist. Wenn Sie beispielsweise feststellen, dass Persp2 5 sein soll, können Sie einfach alle Zellen in der Matrix durch 5 dividieren, was gleich 1 ist Persp2 und das Ergebnis gleich ist.
Aus diesen Gründen Persp2 wird häufig mit 1 festgelegt, was derselbe Wert in der Identitätsmatrix ist.
Persp0 Im Allgemeinen und Persp1 sind kleine Zahlen. Angenommen, Sie beginnen mit einer Identitätsmatrix, legen jedoch auf 0,01 fest Persp0 :
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
Die Transformationsformeln sind:
x' = x / (0,01·x + 1)
y' = y / (0,01·x + 1)
Verwenden Sie nun diese Transformation, um ein quadratisches Feld mit 100 Pixeln am Ursprung zu rendern. So werden die vier Ecken transformiert:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
Wenn x 100 ist, dann ist der Nenner des Z 2, sodass die x- und y-Koordinaten effektiv halbiert werden. Die rechte Seite des Felds wird kürzer als die linke Seite:
Der Persp Teil dieser Zellnamen bezieht sich auf "Perspektive", da die Vorverkürzung nahelegt, dass das Feld jetzt mit der rechten Seite weiter vom Betrachter gekippt wird.
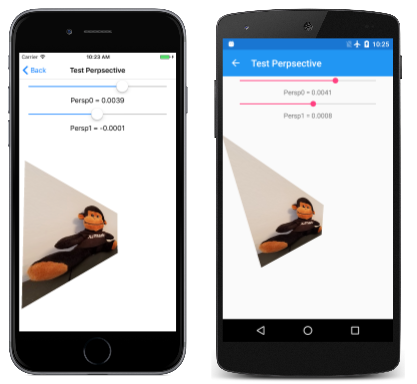
Auf der Seite "Perspektive testen" können Sie mit Werten Persp0 experimentieren und Pers1 ein Gefühl dafür erhalten, wie sie funktionieren. Vernünftige Werte dieser Matrixzellen sind so klein, dass die Slider in der Universelle Windows-Plattform sie nicht ordnungsgemäß verarbeiten kann. Um das UWP-Problem zu berücksichtigen, müssen die beiden Slider Elemente in " TestPerspective.xaml " initialisiert werden, um von –1 bis 1 zu reichen:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Die Ereignishandler für die Schieberegler in der TestPerspectivePage CodeBehind-Datei dividieren die Werte durch 100, sodass sie zwischen -0,01 und 0,01 liegen. Darüber hinaus wird der Konstruktor in einer Bitmap geladen:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
Der PaintSurface Handler berechnet einen SKMatrix Wert, perspectiveMatrix der auf den Werten dieser beiden Schieberegler basiert, dividiert durch 100. Dies wird in Kombination mit zwei Übersetzungstransformationen kombiniert, die die Mitte dieser Transformation in der Mitte der Bitmap platzieren:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
Hier sind einige Beispielbilder:
Während Sie mit den Schiebereglern experimentieren, werden Sie feststellen, dass werte, die über 0,0066 oder unter -0,0066 liegen, dazu führen, dass das Bild plötzlich fraktiert und inkoherent wird. Die transformationierte Bitmap ist 300 Pixel quadratisch. Sie wird relativ zur Mitte des Bitmapbereichs transformiert, sodass die Koordinaten des Bitmapbereichs von -150 bis 150 liegen. Erinnern Sie sich daran, dass der Wert von z' folgendes ist:
z' = Persp0·x + Persp1·y + 1
Wenn Persp0 oder Persp1 größer als 0,0066 oder unter -0,0066 ist, gibt es immer eine Koordinate der Bitmap, die zu einem Z-Wert von Null führt. Dies führt zu Einer Division durch Null, und das Rendering wird zu einem Chaos. Wenn Sie nicht affine Transformationen verwenden, sollten Sie das Rendern von Elementen mit Koordinaten vermeiden, die eine Division durch Null verursachen.
Im Allgemeinen werden Sie nicht festlegen Persp0 und Persp1 isoliert sein. Es ist auch häufig erforderlich, andere Zellen in der Matrix festzulegen, um bestimmte Arten von nicht affinen Transformationen zu erreichen.
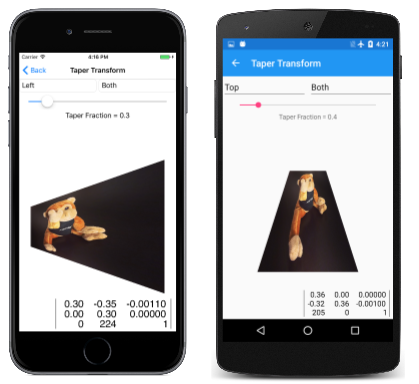
Eine solche nicht affine Transformation ist eine Tapertransformation. Diese Art von nicht affiner Transformation behält die Gesamtabmessungen eines Rechtecks bei, tippt jedoch auf eine Seite:
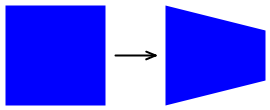
Die TaperTransform Klasse führt eine generalisierte Berechnung einer nicht affinen Transformation basierend auf diesen Parametern aus:
- die rechteckige Größe des zu transformierenden Bilds,
- eine Aufzählung, die die Seite des Rechtecks angibt, das tippt,
- eine weitere Aufzählung, die angibt, wie sie tippt und
- das Ausmaß des Taperings.
Hier ist der -Code:
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
Diese Klasse wird auf der Taper-Transformationsseite verwendet. Die XAML-Datei instanziiert zwei Picker Elemente, um die Enumerationswerte auszuwählen, und eine Slider zum Auswählen des Tipperbruchs. Der PaintSurface Handler kombiniert die Tippertransformation mit zwei Übersetzungstransformationen, um die Transformation relativ zur oberen linken Ecke der Bitmap zu gestalten:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
Im Folgenden finden Sie einige Beispiele:
Eine weitere Art von generalisierten nicht affinen Transformationen ist die 3D-Drehung, die im nächsten Artikel, 3D-Drehungen, veranschaulicht wird.
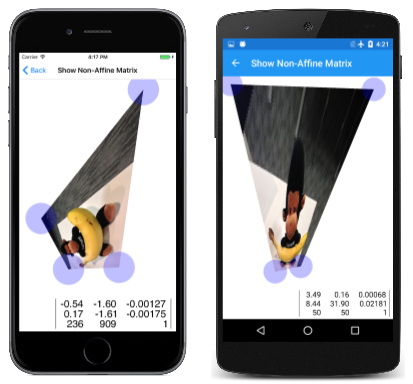
Die nicht affine Transformation kann ein Rechteck in ein beliebiges konvexes Quadrilateral umwandeln. Dies wird auf der Seite "Non-Affine Matrix anzeigen" veranschaulicht. Es ähnelt der Seite "Affine Matrix anzeigen" aus dem Artikel "Matrixtransformationen", mit der Ausnahme, dass es ein viertes TouchPoint Objekt zum Bearbeiten der vierten Ecke der Bitmap enthält:
Solange Sie nicht versuchen, einen Innenwinkel einer der Ecken der Bitmap größer als 180 Grad zu machen oder zwei Seiten miteinander zu kreuzen, berechnet das Programm die Transformation mit dieser Methode aus der ShowNonAffineMatrixPage Klasse erfolgreich:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
Für eine einfache Berechnung erhält diese Methode die Gesamttransformation als Produkt von drei separaten Transformationen, die hier mit Pfeilen symbolisiert werden, die zeigen, wie diese Transformationen die vier Ecken der Bitmap ändern:
(0, 0) → (0, 0) → (0, 0) → (x0, y0) (oben links)
(0, H) → (0, 1) → (0, 1) → (x1, y1) (unten links)
(W, 0) → (1, 0) → (1, 0) → (x2, y2) (oben rechts)
(W, H) → (1, 1) → (a, b) → (x3, y3) (unten rechts)
Die endgültigen Koordinaten rechts sind die vier Punkte, die den vier Berührungspunkten zugeordnet sind. Dies sind die endgültigen Koordinaten der Ecken der Bitmap.
W und H stellen die Breite und Höhe der Bitmap dar. Die erste Transformation S skaliert die Bitmap einfach auf ein Quadrat mit 1 Pixeln. Die zweite Transformation ist die nicht affine Transformation N, und der dritte ist die affine Transformation A. Diese affine Transformation basiert auf drei Punkten, so dass sie genau wie die frühere affine ComputeMatrix Methode ist und die vierte Zeile nicht mit dem (a, b) Punkt umfasst.
Die Werte b und Werte a werden so berechnet, dass die dritte Transformation affin ist. Der Code ruft die Umkehrung der affinen Transformation ab und verwendet diese dann, um die untere rechte Ecke zuzuordnen. Das ist der Punkt (a, b).
Eine weitere Verwendung von nicht affinen Transformationen besteht darin, dreidimensionale Grafiken nachzuahmen. Im nächsten Artikel sehen Sie, wie Sie eine zweidimensionale Grafik im 3D-Raum drehen.