3D-Drehungen in SkiaSharp
Verwenden Sie nicht affine Transformationen, um 2D-Objekte im 3D-Raum zu drehen.
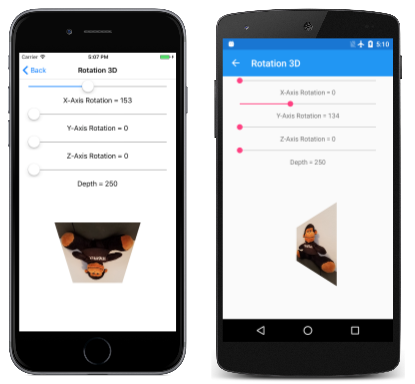
Eine häufige Anwendung von nicht affinen Transformationen ist die Simulation der Drehung eines 2D-Objekts im 3D-Raum:
Dieser Auftrag umfasst das Arbeiten mit dreidimensionalen Drehungen und das Ableiten einer nicht affinen SKMatrix Transformation, die diese 3D-Drehungen ausführt.
Es ist schwer, diese SKMatrix Transformation nur in zwei Dimensionen zu entwickeln. Der Auftrag wird viel einfacher, wenn diese 3:3-Matrix von einer 4:4-Matrix abgeleitet wird, die in 3D-Grafiken verwendet wird. SkiaSharp enthält die SKMatrix44 Klasse für diesen Zweck, aber einige Hintergründe in 3D-Grafiken sind erforderlich, um 3D-Drehungen und die 4-by-4-Transformationsmatrix zu verstehen.
Ein dreidimensionales Koordinatensystem fügt eine dritte Achse namens Z hinzu. Konzeptionell befindet sich die Z-Achse in rechten Winkeln auf dem Bildschirm. Koordinatenpunkte im 3D-Raum werden mit drei Zahlen angegeben: (x, y, z). Im in diesem Artikel verwendeten 3D-Koordinatensystem sind steigende Werte von X nach rechts und die steigenden Werte von Y gehen wie in zwei Dimensionen nach unten. Das Erhöhen positiver Z-Werte kommt aus dem Bildschirm. Der Ursprung ist die obere linke Ecke, genau wie in 2D-Grafiken. Sie können sich den Bildschirm als XY-Ebene mit der Z-Achse in rechten Winkeln zu dieser Ebene vorstellen.
Dies wird als linksseitiges Koordinatensystem bezeichnet. Wenn Sie den Vorfinger für die linke Hand in Richtung positiver X-Koordinaten (nach rechts) zeigen und mit dem Mittleren Finger in die Richtung der Erhöhung der Y-Koordinaten (unten) zeigen, zeigt der Daumen in die Richtung der Erhöhung der Z-Koordinaten – aus dem Bildschirm heraus.
In 3D-Grafiken basieren Transformationen auf einer 4:4-Matrix. Dies ist die 4:4-Identitätsmatrix:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Bei der Arbeit mit einer 4:4-Matrix ist es praktisch, die Zellen mit ihren Zeilen- und Spaltennummern zu identifizieren:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Die SkiaSharp-Klasse Matrix44 ist jedoch etwas anders. Die einzige Möglichkeit zum Festlegen oder Abrufen einzelner Zellwerte SKMatrix44 ist die Verwendung des Item Indexers. Die Zeilen- und Spaltenindizes sind nullbasiert und nicht auf einer Basis, und die Zeilen und Spalten werden ausgetauscht. Auf die Zelle M14 im obigen Diagramm wird mithilfe des Indexers [3, 0] in einem SKMatrix44 Objekt zugegriffen.
In einem 3D-Grafiksystem wird ein 3D-Punkt (x, y, z) in eine 1:4-Matrix konvertiert, um mit der 4:4-Transformationsmatrix zu multiplizieren:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Analog zu 2D-Transformationen, die in drei Dimensionen stattfinden, werden 3D-Transformationen in vier Dimensionen angenommen. Die vierte Dimension wird als W bezeichnet, und der 3D-Raum wird angenommen, dass er innerhalb des 4D-Raums vorhanden ist, wobei W-Koordinaten gleich 1 sind. Die Transformationsformeln sind wie folgt:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Aus den Transformationsformeln ist offensichtlich, dass die Zellen M11M22M33 Skalierungsfaktoren in den Richtungen X, Y und Z und , und , und M41M42M43 sind Übersetzungsfaktoren in den Richtungen X, Y und Z.
Um diese Koordinaten zurück in den 3D-Raum zu konvertieren, wobei W gleich 1 ist, werden die Koordinaten "x", "y" und "z" durch "w" geteilt:
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Diese Division von w' bietet Perspektive im 3D-Raum. Wenn w' gleich 1 ist, tritt keine Perspektive auf.
Drehungen im 3D-Raum können recht komplex sein, aber die einfachsten Drehungen sind die Umdrehungen um die X-, Y- und Z-Achsen. Eine Drehung des Winkels α um die X-Achse ist die folgende Matrix:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Die Werte von X re Standard identisch, wenn sie dieser Transformation unterliegen. Die Drehung um die Y-Achse lässt die Werte von Y unverändert:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
Die Drehung um die Z-Achse entspricht in 2D-Grafiken:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Die Drehrichtung wird durch die Übergabe des Koordinatensystems impliziert. Dies ist ein linkshändiges System. Wenn Sie also den Daumen der linken Hand auf die Erhöhung der Werte für eine bestimmte Achse zeigen – nach rechts zur Drehung um die X-Achse, nach unten für Drehung um die Y-Achse und für Drehung um die Z-Achse – dann gibt die Kurve der anderen Finger die Drehrichtung für positive Winkel an.
SKMatrix44 verfügt über generalisierte statische CreateRotation Und CreateRotationDegrees Methoden, mit denen Sie die Achse angeben können, um die die Drehung erfolgt:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Legen Sie für drehung um die X-Achse die ersten drei Argumente auf 1, 0, 0 fest. Legen Sie die Drehung um die Y-Achse auf 0, 1, 0 und für drehung um die Z-Achse auf 0, 0, 1 fest.
Die vierte Spalte der 4:4 ist für die Perspektive vorgesehen. Die SKMatrix44 Methode hat keine Methoden zum Erstellen von perspektivisch transformierten Transformationen, sie können jedoch selbst mit dem folgenden Code erstellt werden:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
Der Grund für den Argumentnamen depth wird in Kürze offensichtlich sein. Dieser Code erstellt die Matrix:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Die Transformationsformeln führen zu der folgenden Berechnung von w':
w' = –z / depth + 1
Dies dient dazu, X- und Y-Koordinaten zu reduzieren, wenn die Werte von Z kleiner als null sind (konzeptionell hinter der XY-Ebene) und X- und Y-Koordinaten für positive Werte von Z zu erhöhen. Wenn die Z-Koordinate gleich ist depth, ist w' null, und Koordinaten werden unendlich. Dreidimensionale Grafiksysteme basieren auf einer Kamerametapher, und der depth Wert hier stellt den Abstand der Kamera vom Ursprung des Koordinatensystems dar. Wenn ein grafisches Objekt eine Z-Koordinate aufweist, die Einheiten vom Ursprung ist depth , berührt es konzeptionell das Objektiv der Kamera und wird unendlich groß.
Denken Sie daran, dass Sie diesen perspectiveMatrix Wert wahrscheinlich in Kombination mit Drehmatrizen verwenden werden. Wenn ein grafikobjekt, das gedreht wird, X- oder Y-Koordinaten größer als depthist, ist die Drehung dieses Objekts im 3D-Raum wahrscheinlich Z-Koordinaten größer als depth. Dies muss vermieden werden! Beim Erstellen perspectiveMatrix möchten Sie einen Wert festlegen depth , der für alle Koordinaten im Grafikobjekt ausreichend groß ist, unabhängig davon, wie es gedreht wird. Dadurch wird sichergestellt, dass es nie eine Division durch Null gibt.
Das Kombinieren von 3D-Drehungen und Perspektiven erfordert eine Multiplikation von 4-mal-4-Matrizen. Zu diesem Zweck SKMatrix44 werden Verkettungsmethoden definiert. Wenn A und B objekte sind SKMatrix44 , legt der folgende Code A auf A × B fest:
A.PostConcat(B);
Wenn eine 4:4-Transformationsmatrix in einem 2D-Grafiksystem verwendet wird, wird sie auf 2D-Objekte angewendet. Diese Objekte sind flach und werden davon ausgegangen, dass Z-Koordinaten null sind. Die Transformationsmultiplizierung ist etwas einfacher als die zuvor gezeigte Transformation:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Dieser Wert für z führt zu Transformationsformeln, die keine Zellen in der dritten Zeile der Matrix enthalten:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Darüber hinaus ist die Z-Koordinate auch hier irrelevant. Wenn ein 3D-Objekt in einem 2D-Grafiksystem angezeigt wird, wird es durch Ignorieren der Z-Koordinatenwerte auf ein zweidimensionales Objekt reduziert. Die Transformationsformeln sind wirklich diese beiden:
x" = x' / w'
y" = y' / w'
Dies bedeutet, dass die dritte Zeile und dritte Spalte der 4:4-Matrix ignoriert werden kann.
Aber wenn ja, warum ist die 4-by-4-Matrix sogar in erster Linie erforderlich?
Obwohl die dritte Zeile und dritte Spalte der 4:4 für zweidimensionale Transformationen irrelevant sind, spielen die dritte Zeile und Spalte eine Rolle, bevor verschiedene SKMatrix44 Werte miteinander multipliziert werden. Angenommen, Sie multiplizieren die Drehung um die Y-Achse mit der perspektivische Transformation:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
Im Produkt enthält die Zelle M14 nun einen perspektivische Wert. Wenn Sie diese Matrix auf 2D-Objekte anwenden möchten, werden die dritte Zeile und Spalte entfernt, um sie in eine 3:3-Matrix zu konvertieren:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Jetzt kann es verwendet werden, um einen 2D-Punkt zu transformieren:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Die Transformationsformeln sind:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Teilen Sie nun alles durch z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Wenn 2D-Objekte mit einem positiven Winkel um die Y-Achse gedreht werden, werden positive X-Werte auf den Hintergrund zurückgerückt, während negative X-Werte in den Vordergrund gelangen. Die X-Werte scheinen sich näher an der Y-Achse (die durch den Kosinuswert gesteuert wird) näher zu bewegen, da Koordinaten, die von der Y-Achse am weitesten entfernt sind, kleiner oder größer werden, wenn sie vom Betrachter oder näher an den Betrachter heranziehen.
Führen Sie bei Verwendung SKMatrix44alle 3D-Drehungs- und Perspektivenvorgänge aus, indem Sie verschiedene SKMatrix44 Werte multiplizieren. Anschließend können Sie mithilfe der Eigenschaft der SKMatrix44 Klasse eine zweidimensionale 3:3-Matrix aus der 4:4-Matrix Matrix extrahieren. Diese Eigenschaft gibt einen vertrauten SKMatrix Wert zurück.
Auf der Seite "Drehung 3D " können Sie mit der 3D-Drehung experimentieren. Die Datei Rotation3DPage.xaml instanziiert vier Schieberegler, um die Drehung um die X-, Y- und Z-Achsen festzulegen und einen Tiefenwert festzulegen:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Beachten Sie, dass die depthSlider Initialisierung mit dem Minimum Wert 250 erfolgt. Dies bedeutet, dass das hier gedrehte 2D-Objekt X- und Y-Koordinaten auf einen Kreis beschränkt hat, der durch einen Radius von 250 Pixeln um den Ursprung definiert ist. Jede Drehung dieses Objekts im 3D-Raum führt immer zu Koordinatenwerten unter 250.
Die Rotation3DPage.cs CodeBehind-Datei wird in einer Bitmap geladen, die 300 Pixel groß ist:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Wenn die 3D-Transformation auf dieser Bitmap zentriert ist, liegen X- und Y-Koordinaten zwischen -150 und 150, während die Ecken 212 Pixel vom Mittelpunkt liegen, sodass sich alles innerhalb des Radius von 250 Pixeln befindet.
Der PaintSurface Handler erstellt SKMatrix44 Objekte basierend auf den Schiebereglern und multipliziert sie mithilfe von PostConcat. Der SKMatrix aus dem endgültigen SKMatrix44 Objekt extrahierte Wert wird von Transformationen umgeben, um die Drehung in der Mitte des Bildschirms zu zentrieren:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Wenn Sie mit dem vierten Schieberegler experimentieren, werden Sie feststellen, dass die unterschiedlichen Tiefeneinstellungen das Objekt nicht weiter weg vom Betrachter verschieben, sondern stattdessen den Umfang des perspektivisch wirken:
Die animierte Drehung 3D verwendet SKMatrix44 auch zum Animieren einer Textzeichenfolge im 3D-Raum. Der textPaint Objektsatz als Feld wird im Konstruktor verwendet, um die Grenzen des Texts zu bestimmen:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Die OnAppearing Außerkraftsetzung definiert drei Xamarin.FormsAnimation Objekte, um die xRotationDegreesFelder yRotationDegreeszRotationDegrees mit unterschiedlichen Geschwindigkeiten zu animieren. Beachten Sie, dass die Punkte dieser Animationen auf Primzahlen (5 Sekunden, 7 Sekunden und 11 Sekunden) festgelegt sind, sodass die Gesamtkombination nur alle 385 Sekunden oder mehr als 10 Minuten wiederholt wird:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Wie im vorherigen Programm erstellt SKMatrix44 der PaintCanvas Handler Werte für Drehung und Perspektive und multipliziert sie zusammen:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Diese 3D-Drehung ist von mehreren 2D-Transformationen umgeben, um den Drehmittelpunkt in die Mitte des Bildschirms zu verschieben und die Größe der Textzeichenfolge so zu skalieren, dass sie die gleiche Breite wie der Bildschirm hat: