Auswertung von Wahrscheinlichkeitsfunktionen
Wichtig
Der Support für Machine Learning Studio (klassisch) endet am 31. August 2024. Es wird empfohlen, bis zu diesem Datum auf Azure Machine Learning umzustellen.
Ab dem 1. Dezember 2021 können Sie keine neuen Ressourcen in Machine Learning Studio (klassisch) mehr erstellen. Bis zum 31. August 2024 können Sie die vorhandenen Ressourcen in Machine Learning Studio (klassisch) weiterhin verwenden.
- Siehe Migrieren zu Azure Machine Learning
- Weitere Informationen zu Azure Machine Learning.
Die Dokumentation zu ML Studio (klassisch) wird nicht mehr fortgeführt und kann künftig nicht mehr aktualisiert werden.
Passt eine angegebene Wahrscheinlichkeitsverteilungsfunktion auf ein Dataset an.
Kategorie: Statistische Funktionen
Hinweis
Giltnur für: Machine Learning Studio (klassisch)
Ähnliche Drag & Drop-Module sind im Azure Machine Learning-Designer verfügbar.
Modulübersicht
In diesem Artikel wird beschrieben, wie Sie das Modul "Wahrscheinlichkeitsfunktion auswerten" in Machine Learning Studio (klassisch) verwenden, um statistische Kennzahlen zu berechnen, die die Verteilung einer Spalte beschreiben, z. B. die Bernoulli-, Pareto- oder Poisson-Verteilungen.
Um dieses Modell zu verwenden, verbinden Sie ein Dataset, das mindestens eine Spalte numerischer Werte enthält, und wählen Sie eine Wahrscheinlichkeitsverteilung aus, die getestet werden soll. Das Modul gibt eine Datentabelle zurück, die Werte aus der angegebenen Wahrscheinlichkeitsfunktion enthält.
Sie können eine der folgenden Werte für die ausgewählte Wahrscheinlichkeitsverteilung berechnen:
- Kumulative Verteilungsfunktion (cdf)
- Umgekehrte kumulative Verteilungsfunktion (InverseCdf)
- Wahrscheinlichkeitsdichtefunktion (Pdf)
Warum ist die Wahrscheinlichkeitsverteilung nützlich?
Wenn Sie Ihre Daten anhand einer Wahrscheinlichkeitsverteilung auswerten, weisen Sie Spaltenwerte einer Gruppe von Werten mit bekannten Eigenschaften zu. Wenn Sie wissen, ob Ihre Daten einer dieser bekannten Verteilungen entsprechen, können Sie möglicherweise andere Eigenschaften Ihrer Daten ableiten. Im Allgemeinen können Sie bessere Vorhersagen von einem Modell erhalten, wenn Sie die Verteilung ermitteln können, die für die Daten am besten geeignet ist.
Die Antwort auf die Frage nach der zu verwendenden Wahrscheinlichkeitsverteilungsfunktion hängt sowohl von den Daten als auch von den Variablen ab, die gemessen werden. Beispielsweise sind einige Verteilungen so konzipiert, dass Wahrscheinlichkeiten von diskreten Werten beschrieben werden; andere sind nur für die Verwendung mit fortlaufenden numerischen Variablen vorgesehen. Für einige Verteilungen müssen Sie auch im Voraus ein erwartetes Mittel, ein Maß an Freiheit usw. kennen. Ausführliche Informationen finden Sie unter Unterstützte Wahrscheinlichkeitsverteilungen
Konfigurieren der Bewertungswahrscheinlichkeitsfunktion
Alle Optionen ändern sich je nach Art der Wahrscheinlichkeitsverteilung, die Sie berechnen möchten. Wenn Sie die Wahrscheinlichkeitsverteilungsmethode ändern, werden andere Auswahlen, die Sie möglicherweise vorgenommen haben, zurückgesetzt.
Achten Sie daher darauf, zuerst die Option "Verteilung " auszuwählen!
Das dataset, das als Eingabe verwendet wird, sollte numerische Daten enthalten. Andere Datentypen werden ignoriert.
Für jede Analyse können Sie eine einzelne Wahrscheinlichkeitsverteilungsmethode anwenden. Um eine andere Wahrscheinlichkeitsverteilung zu berechnen, fügen Sie eine separate Instanz des Moduls für jede Verteilung hinzu, die Sie testen möchten.
Fügen Sie dem Experiment das Modul "Wahrscheinlichkeitsfunktion auswerten " hinzu. Dieses Modul finden Sie in der Kategorie "Statistische Funktionen" in Machine Learning Studio (klassisch).
Verbinden ein Dataset, das mindestens eine Spalte mit Zahlen enthält.
Verwenden Sie die Option "Verteilung" , um die Art der Wahrscheinlichkeitsverteilung auszuwählen, die Sie berechnen möchten. Siehe Unterstützte Wahrscheinlichkeitsverteilungen für eine Liste der Optionen und deren erforderliche Argumente.
Legen Sie alle Parameter fest, die für die Verteilung erforderlich sind.
Wählen Sie eine der drei zu erstellenden Statistiken aus: die kumulative Verteilungsfunktion (cdf), die umgekehrte kumulative Verteilungsfunktion (InverseCdf) oder die Wahrscheinlichkeitsdichtefunktion (pdf).
Weitere Informationen finden Sie im Abschnitt "Technische Hinweise " zu Definitionen.
Verwenden Sie die Spaltenauswahl, um die Spalten auszuwählen, über die die ausgewählte Wahrscheinlichkeitsverteilung berechnet werden soll.
Alle ausgewählten Spalten müssen über einen numerischen Datentyp verfügen.
Der Datenbereich in der Spalte muss für die ausgewählte Wahrscheinlichkeitsfunktion ebenfalls gültig sein. Andernfalls kann ein Fehler oder ein NaN-Ergebnis auftreten.
Bei Spalten mit geringer Dichte werden alle Werte, die Hintergrundnullen entsprechen, nicht verarbeitet.
Verwenden Sie die Option "Ergebnismodus" , um anzugeben, wie die Ergebnisse ausgegeben werden. Sie können die Spaltenwerte durch die Werte für die Wahrscheinlichkeitsverteilung ersetzen, die neuen Werte an das Dataset anfügen oder nur die Werte für die Wahrscheinlichkeitsverteilung zurückgeben.
Führen Sie das Experiment aus, oder klicken Sie mit der rechten Maustaste auf das Modul "Wahrscheinlichkeitsfunktion auswerten ", und klicken Sie auf " Ausführen".
Ergebnisse
Die folgende Tabelle enthält ein Beispiel für Ergebnisse mit der Option "Anfügen " in einer einzelnen Temperaturspalte aus dem Beispieldatensatz "Forest Fires ".
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp) | FFisher.cdf(temp) |
|---|---|---|---|---|
| 8,2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11.4 | 1 | 1 | 0.993147 | 0.001502 |
Die Überschriften der generierten Spalten enthalten die Wahrscheinlichkeitsverteilung, die verwendet wurde.
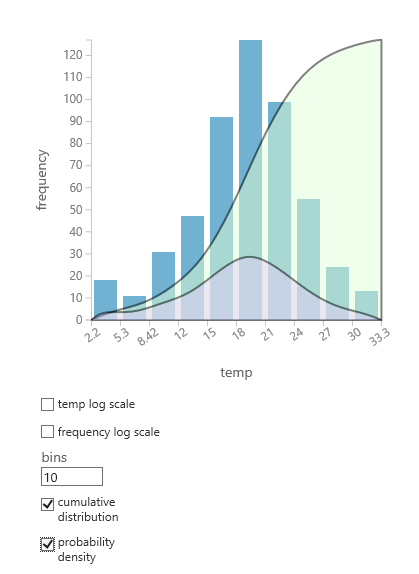
Wenn Sie nicht sicher sind, welche Wahrscheinlichkeitsverteilung für Ihre Daten geeignet ist, können Sie ein schnelles Diagramm der kumulativen Verteilung und Wahrscheinlichkeitsdichte für jede numerische Spalte erstellen.
- Klicken Sie mit der rechten Maustaste auf das Dataset oder die Modulausgabe, und wählen Sie "Visualisieren" aus.
- Wählen Sie die Interessenspalte aus, und wählen Sie im Histogrammbereichdie kumulative Verteilung oder Wahrscheinlichkeitsdichte aus.
- Ein Diagramm der Verteilung wird wie folgt auf dem Histogramm überlagert, das die Daten darstellt.
Unterstützte Wahrscheinlichkeitsverteilungen
Das Modul "Wahrscheinlichkeitsfunktion auswerten " unterstützt die folgenden Verteilungen:
Bernoulli
Die Bernoulli-Verteilung ist eine Verteilung über binäre Werte: Mit anderen Worten, sie modelliert die erwartete Verteilung, wenn nur zwei Werte möglich sind.
Um zu berechnen, wählen Sie Bernoulli aus, und legen Sie die folgenden Optionen fest:
- Probability of success
Der Parameter p gibt die Wahrscheinlichkeit an, dass eine 1 generiert wird. Geben Sie eine Zahl (float) zwischen 0,0 und 1,0 ein, die die Erfolgswahrscheinlichkeit angibt. Der Standardwert ist .5.
Beta
Die Beta-Verteilung ist eine kontinuierliche univariate Verteilung.
Um zu berechnen, wählen Sie Beta aus, und legen Sie die folgenden Optionen fest:
Form
Geben Sie einen Wert ein, um die Form der Verteilung zu ändern.Ein Formparameter ist ein beliebiger Parameter einer Wahrscheinlichkeitsverteilung, der weder die Position noch die Skalierung definiert. Wenn Sie also einen Wert für die Form eingeben, ändert der Parameter die Form der Verteilung, statt sie zu verschieben, zu vergrößern oder zu verkleinern.
Der Wert muss eine Zahl (
double) sein. Der Standardwert ist 1.0.Skalierung
Geben Sie eine Zahl ein, die für die Skalierung der Verteilung verwendet werden soll.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Obergrenze
Geben Sie eine Zahl (double) ein, die die obere Grenze der Verteilung darstellt. Der Standardwert ist 1.0.Unterer Grenzwert
Geben Sie eine Zahl (double) ein, die die untere Grenze der Verteilung darstellt. Der Standard ist 0,0.
Binomial
Die Binomialverteilung ist eine diskrete univariate Verteilung. Die Binomial-Verteilung wird verwendet, um die Anzahl der Erfolge in einer Stichprobe zu modellieren. Das Zurücklegen wird bei der Stichprobenentnahme verwendet. Verwenden Sie bei der Stichprobenentnahme ohne Zurücklegung die hypergeometrische Verteilung.
Um zu berechnen, wählen Sie Binomial aus, und legen Sie die folgenden Optionen fest:
Probability of success
Geben Sie eine Zahl (float) zwischen 0,0 und 1,0 ein, die die Erfolgswahrscheinlichkeit angibt. Der Standardwert ist .5.Number of trials
Geben Sie die Anzahl der Versuche an.Verwenden Sie ein
integer, mit einem Mindestwert von 1. Der Standardwert ist 3.
Cauchy
Die Cauchy-Verteilung ist eine symmetrische kontinuierliche Wahrscheinlichkeitsverteilung.
Um zu berechnen, wählen Sie Cauchy aus, und legen Sie die folgenden Optionen fest:
Location
Geben Sie eine Zahl (double) ein, die die Position des 0.- Elements darstellt.Durch die Angabe eines Werts für den Parameter Speicherort können Sie die Wahrscheinlichkeitsverteilung um eine numerische Dezimalstelle nach oben oder unten verschieben.
Der Standard ist 0,0.
ChiSquare
Die chi-quadratische Verteilung ist eine Summe der Quadrate von k unabhängig, Standard, normal, Zufallsvariablen.
Zum Berechnen wählen Sie ChiSquare aus, und legen Sie die folgenden Optionen fest:
- Anzahl der Freiheitsgrade Geben Sie eine Zahl (
double) ein, um den Freiheitsgrad anzugeben. Der Standardwert ist 1.0.
ChiSquareRightTailed
Diese Option bietet eine rechtsseitige chi-quadratische Verteilung.
Um zu berechnen, wählen Sie ChiSquareRightTailed aus, und legen Sie die folgenden Optionen fest:
- Number of degrees of freedom
Geben Sie eine Zahl (double) ein, um den Freiheitsgrad anzugeben. Der Standardwert ist 1.0.
Exponentiell
Die Exponentialverteilung ist eine Verteilung über die reellen Zahlen, die durch einen nicht negativen Parameter parametrisiert wird.
Um zu berechnen, wählen Sie "Exponentielle" aus, und legen Sie die folgenden Optionen fest:
- Lambda
Geben Sie eine Zahl (double) ein, die als Lambda-Parameter verwendet wird. Der Standardwert ist 1.0.
FFisher
Generiert die Wahrscheinlichkeit der Fisher-Statistik für eine Stichprobe, auch bekannt als Fisher F-Verteilung. Bei dieser Verteilung handelt es sich um eine zweiseitige Verteilung.
Um zu berechnen, wählen Sie FFisher aus, und legen Sie die folgenden Optionen fest:
Numerator degrees of freedom
Geben Sie eine Zahl (double) ein, um die im Zähler zu verwendenden Freiheitsgrade anzugeben. Der Standardwert ist 3.0.Denominator degrees of freedom
Geben Sie eine Zahl (double) ein, um die im Nenner zu verwendenden Freiheitsgrade anzugeben. Der Standardwert ist 6.0.
FFisherRightTailed
Erstellt eine rechtsseitige Fisher-Verteilung. Die Fisher-Verteilung ist auch als Fisher-F-Verteilung, Snedecor-Verteilung oder Fisher-Snedecor-Verteilung bekannt. Diese Verteilungsform ist rechtsseitig.
Um zu berechnen, wählen Sie FFisherRightTailed aus, und legen Sie die folgenden Optionen fest:
Numerator degrees of freedom
Geben Sie eine Zahl (double) ein, um die im Zähler zu verwendenden Freiheitsgrade anzugeben. Der Standardwert ist 3.0.Denominator degrees of freedom
Geben Sie eine Zahl (double) ein, um die im Nenner zu verwendenden Freiheitsgrade anzugeben. Der Standardwert ist 6.0.
Gamma
Die Gamma-Verteilung ist eine Reihe von kontinuierlichen Wahrscheinlichkeitsverteilungen mit zwei Parametern. Chi-Quadrat ist z. B. ein Sonderfall der Gamma-Verteilung.
Um Gamma zu berechnen, wählen Sie Gamma aus, und legen Sie die folgenden Optionen fest:
Skalierung
Geben Sie einen Wert für die Skalierung der Verteilung ein.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Location
Geben Sie eine Zahl (double) ein, die die Position des 0.- Elements darstellt.Durch die Angabe eines Werts für den Parameter Speicherort können Sie die Wahrscheinlichkeitsverteilung um eine numerische Dezimalstelle nach oben oder unten verschieben.
Der Standard ist 0,0.
GeneralizedExtremeValues
Erstellt eine Verteilung, die entwickelt wurde, um extreme Werte zu behandeln. Die generalisierte Extremwertverteilung (GEV) ist tatsächlich eine Gruppe kontinuierlicher Wahrscheinlichkeitsverteilungen, die die Gumbel-, Fréchet- und Weibull-Verteilungen (auch als Typ I, II und III extreme Wertverteilungen bezeichnet) kombiniert.
Weitere Informationen zur Theorie extremer Werte finden Sie in diesem Artikel in Wikipedia: Fisher-Tippet-Gnedenko theorem.
Um zu berechnen, wählen Sie GeneralizedExtremeValues aus, und legen Sie die folgenden Optionen fest:
Form
Geben Sie einen Wert ein, um die Form der Verteilung zu ändern.Ein Formparameter ist ein beliebiger Parameter einer Wahrscheinlichkeitsverteilung, der weder die Position noch die Skalierung definiert. Wenn Sie also einen Wert für die Form eingeben, ändert der Parameter die Form der Verteilung, statt sie zu verschieben, zu vergrößern oder zu verkleinern.
Der Wert muss eine Zahl (
double) sein. Der Standardwert ist 1.0.Skalierung
Geben Sie einen Wert für die Skalierung der Verteilung ein.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Location
Geben Sie eine Zahl (double) ein, die die Positiondes 0. Elements darstellt.Durch die Eingabe eines Werts für den Parameter Location können Sie die Wahrscheinlichkeitsverteilung um eine numerische Dezimalstelle nach oben oder unten verschieben.
Der Standard ist 0,0.
Geometrischer
Die geometrische Verteilung ist eine Verteilung über positive ganze Zahlen, die durch eine positive reale Zahl parameterisiert werden.
Um zu berechnen, wählen Sie "Geometrische" aus, und legen Sie die folgenden Optionen fest:
- Probability of success
Geben Sie eine Zahl (float) zwischen 0,0 und 1,0 ein, die die Erfolgswahrscheinlichkeit angibt. Der Standardwert ist .5.
Hinweis
Diese Implementierung der geometrischen Verteilung generiert keine Nullen.
GumbelMax
Die Gumbel-Verteilung ist eine von mehreren Extremwertverteilungen. Die GumbelMax-Option implementiert die maximale Extremwertverteilung des Typs 1.
Um zu berechnen, wählen Sie GumbelMax aus, und legen Sie die folgenden Optionen fest:
Skalierung
Geben Sie einen Wert für die Skalierung der Verteilung ein.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Location
Geben Sie eine Zahl (double) ein, die die Positiondes 0. Elements darstellt.Durch die Eingabe eines Werts für den Parameter Location können Sie die Wahrscheinlichkeitsverteilung um eine numerische Dezimalstelle nach oben oder unten verschieben.
Der Standard ist 0,0.
GumbelMin
Die Gumbel-Verteilung ist eine von mehreren Extremwertverteilungen. Die Gumbel-Verteilung wird auch als die kleinste Extremwertverteilung (SEV, Smallest Extreme Value distribution) oder kleinste Extremwertverteilung (Typ I) bezeichnet. Die Option GumbelMin implementiert die Verteilung des Minimum Extreme Value Typ 1.
Um zu berechnen, wählen Sie GumbelMin aus, und müssen die folgenden Optionen festlegen:
Skalierung
Geben Sie einen Wert für die Skalierung der Verteilung ein.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Location
Geben Sie eine Zahl (double) ein, die die Positiondes 0. Elements darstellt.Durch die Eingabe eines Werts für den Parameter Location können Sie die Wahrscheinlichkeitsverteilung um eine numerische Dezimalstelle nach oben oder unten verschieben.
Der Standard ist 0,0.
Hypergeometric
Die Hypergeometrische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die die Anzahl der Erfolge in einer Sequenz von n aus einer endlichen Bevölkerung ohne Ersatz beschreibt, genauso wie die Binomialverteilung die Anzahl der Erfolge für Zeichnungen mit Ersatz beschreibt.
Um zu berechnen, wählen Sie Hypergeometrisch aus, und legen Sie die folgenden Optionen fest:
Anzahl der Beispiele
Geben Sie eine ganze Zahl ein, die die Anzahl der zu verwendenden Stichproben angibt. Der Standardwert ist 9.Number of success
Geben Sie eine ganze Zahl ein, die den Erfolgswert angibt. Der Standardwert ist 24.Population size
Geben Sie die Größe der Grundgesamtheit an, die beim Schätzen der hypergeometrischen Verteilung verwendet werden soll.
Laplace
Die Laplace-Verteilung ist eine Verteilung über die realen Zahlen, die durch ein Mittel und durch einen Skalierungsparameter parameterisiert werden.
Um zu berechnen, wählen Sie die Laplace-Verteilung aus, und legen Sie die folgenden Optionen fest:
Skalierung
Geben Sie einen Wert für die Skalierung der Verteilung ein.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Location
Geben Sie eine Zahl (double) ein, die die Positiondes 0. Elements darstellt.Durch die Eingabe eines Werts für den Parameter Location können Sie die Wahrscheinlichkeitsverteilung um eine numerische Dezimalstelle nach oben oder unten verschieben.
Der Standard ist 0,0.
Logik
Die logistische Verteilung ähnelt der Normalverteilung, hat jedoch auf der linken Seite der Verteilung keine Beschränkung. Die logistische Verteilung wird bei der logistischen Regression und bei Modellen neuronaler Netzwerke sowie für die Modellierung von biowissenschaftlichen Daten verwendet.
Um zu berechnen, wählen Sie Logistik aus, und legen Sie die folgenden Optionen fest:
Skalierung
Geben Sie einen Wert für die Skalierung der Verteilung ein.Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.
Der Standardwert ist 1,0. Werte müssen positive Zahlen sein.
Mean
Geben Sie eine Zahl (double) ein, die den geschätzten Mittelwert der Verteilung angibt. Der Standard ist 0,0.
Lognormal
Die Lognormal-Verteilung ist eine kontinuierliche univariate Verteilung.
Um zu berechnen, wählen Sie Lognormal aus, und legen Sie die folgenden Optionen fest:
Mean
Geben Sie eine Zahl (double) ein, die den geschätzten Mittelwert der Verteilung angibt. Der Standard ist 0,0.Standardabweichung
Geben Sie eine positive Zahl (double) ein, die die geschätzte Standardabweichung der Verteilung angibt. Der Standardwert ist 1.0.
NegativeBinomial
Die negative binomiale Verteilung ist eine Verteilung über die natürlichen Zahlen mit zwei Parametern (r, p). Im speziellen Fall, der r eine ganze Zahl ist, können Sie die Verteilung als Die Anzahl der Tails vor demr-Kopf interpretieren, wenn die Wahrscheinlichkeit des Kopfes p ist.
Um zu berechnen, wählen Sie NegativeBinomial aus, und legen Sie die folgenden Optionen fest:
Probability of success
Geben Sie eine Zahl (float) zwischen 0,0 und 1,0 ein, die die Erfolgswahrscheinlichkeit angibt. Der Standardwert ist .5.Number of success
Geben Sie eine ganze Zahl ein, die den Erfolgswert angibt. Der Standardwert ist 24.
Normal
Die Normalverteilung wird auch als gaussische Verteilung bezeichnet.
Um zu berechnen, wählen Sie "Normal" aus, und legen Sie die folgenden Optionen fest:
Mean
Geben Sie eine Zahl (double) ein, die den geschätzten Mittelwert der Verteilung angibt. Der Standard ist 0,0.Standardabweichung
Geben Sie eine positive Zahl (double) ein, die die geschätzte Standardabweichung der Verteilung angibt. Der Standardwert ist 1.0.
Pareto
Die Pareto-Verteilung ist eine Potenzgesetz-Wahrscheinlichkeitsverteilung, die zur Beschreibung von sozialen, wissenschaftlichen, geophysikalischen, versicherungsmathematischen und vielen anderen zu beobachtenden Phänomenen dient.
Um zu berechnen, wählen Sie Pareto aus, und legen Sie die folgenden Optionen fest:
Form
Geben Sie einen Wert ein (optional), um die Form der Verteilung zu ändern.Ein Formparameter ist ein beliebiger Parameter einer Wahrscheinlichkeitsverteilung, der weder die Position noch die Skalierung definiert. Wenn Sie also einen Wert für die Form eingeben, ändert der Parameter die Form der Verteilung, statt sie zu verschieben, zu vergrößern oder zu verkleinern.
Der Wert muss eine Zahl (
double) sein. Der Standardwert ist 1.0.Skalierung
Geben Sie einen Wert (optional) ein, um die Skalierung der Verteilung zu ändern. Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.Der Wert muss eine Zahl (
double) sein. Der Standardwert ist 1.0.
Poisson
In dieser Implementierung wird die Knuth-Methode zum Generieren von poissonverteilten Zufallsvariablen verwendet. Weitere Informationen zur Poisson-Verteilung finden Sie unter Poisson Regression.
Zum Berechnen wählen Sie Poisson aus, und legen Sie die folgenden Optionen fest:
- Mean
Geben Sie eine Zahl (double) ein, die den geschätzten Mittelwert der Verteilung angibt. Der Standard ist 0,0.
Rayleigh
Die Rayleigh-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Als Beispiel dafür, wie diese entsteht, verfügt die Windgeschwindigkeit über eine Rayleigh-Verteilung, wenn die Komponenten des zweidimensionalen Windgeschwindigkeitsvektors unkorreliert und mit gleicher Varianz normalverteilt sind.
Um zu berechnen, wählen Sie Rayleigh aus, und legen Sie die folgenden Optionen fest:
- Unterer Grenzwert
Geben Sie eine Zahl (double) ein, die die untere Grenze der Verteilung darstellt. Der Standard ist 0,0.
StandardNormal
Diese Option stellt die Standardnormalverteilung ohne andere Parameter bereit.
Um zu berechnen, wählen Sie "StandardNormal" aus, und wählen Sie die Spalten aus.
TStudent
Diese Option implementiert die t-Verteilung des univariate Student.
Um zu berechnen, wählen Sie TStudent aus, und legen Sie die folgenden Optionen fest:
- Number of degrees of freedom
Geben Sie eine Zahl (double) ein, um den Freiheitsgrad anzugeben. Der Standardwert ist 1.0.
TStudentRightTailed
Implementiert die univariate rechtsseitige Student-t-Verteilung.
Um zu berechnen, wählen Sie TStudentRightTailed aus, und legen Sie die folgenden Optionen fest:
- Number of degrees of freedom
Geben Sie eine Zahl (double) ein, um den Freiheitsgrad anzugeben. Der Standardwert ist 1.0.
TStudentTwoTailed
Implementiert eine zweiseitige Student-t-Verteilung.
Um zu berechnen, wählen Sie TStudentTwoTailed aus, und legen Sie die folgenden Optionen fest:
- Number of degrees of freedom
Geben Sie eine Zahl (double) ein, um den Freiheitsgrad anzugeben. Der Standardwert ist 1.0.
Uniform
Die Gleichverteilung ist auch als Rechteckverteilung bekannt.
Um zu berechnen, wählen Sie "Uniform" aus, und legen Sie die folgenden Optionen fest:
Unterer Grenzwert
Geben Sie eine Zahl (double) ein, die die untere Grenze der Verteilung darstellt. Der Standard ist 0,0.Obergrenze
Geben Sie eine Zahl (double) ein, die die obere Grenze der Verteilung darstellt. Der Standardwert ist 1.0.
Weibull
Die Weibull-Verteilung wird häufig in der Zuverlässigkeitsüberwachung verwendet. Sie können den Shape-Parameter verwenden, um viele andere Verteilungen zu modellieren.
Um zu berechnen, wählen Sie Weibull aus, und legen Sie die folgenden Optionen fest:
Form
Geben Sie einen Wert ein (optional), um die Form der Verteilung zu ändern.Ein Formparameter ist ein beliebiger Parameter einer Wahrscheinlichkeitsverteilung, der weder die Position noch die Skalierung definiert. Wenn Sie also einen Wert für die Form eingeben, ändert der Parameter die Form der Verteilung, statt sie zu verschieben, zu vergrößern oder zu verkleinern.
Der Wert muss eine Zahl (
double) sein. Der Standardwert ist 1.0.Skalierung
Geben Sie einen Wert (optional) ein, um die Skalierung der Verteilung zu ändern. Wenn Sie einen Skalierungswert für die Verteilung verwenden, können Sie diesen verkleinern oder vergrößern.Der Wert muss eine Zahl (
double) sein. Der Standardwert ist 1.0.
Technische Hinweise
Dieser Abschnitt enthält Implementierungsdetails, Tipps und Antworten auf häufig gestellte Fragen.
Details zur Implementierung
Dieses Modul unterstützt alle Verteilungen, die in der Open Source-MATH.NET Numerics-Bibliothek bereitgestellt sind. Weitere Informationen finden Sie in der Dokumentation für die Math.Net.Numerics.Distribution-Bibliothek .
Rechtsseitige und zweiseitige Verteilungen werden als separate Verteilungen angezeigt, nicht als parametrisierte Versionen von Basisverteilungen. Das aktuelle Verhalten gewährleistet die Kompatibilität mit Excel.
Definitionen
Dieses Modul unterstützt die Berechnung einer dieser Werte für die angegebene Verteilung:
cdf oder die kumulative Verteilungsfunktion
Gibt die Wahrscheinlichkeit für ein zusammengesetztes Ereignis zurück, das als Summe von Ocurrences definiert wird, wenn die Zufallsvariable einen Wert verwendet, der kleiner als einige bestimmte Werte x ist.
Anders ausgedrückt, beantwortet sie die Frage: "Wie häufig sind Beispiele, die kleiner oder gleich diesem Wert sind?"
Diese Funktion kann sowohl mit fortlaufenden als auch mit diskreten numerischen Variablen verwendet werden.
UmgekehrteCdf oder die umgekehrte kumulative Verteilungsfunktion
Gibt den Wert zurück, der einem bestimmten kumulativen Wahrscheinlichkeitswert (cdf) zugeordnet ist.
Anders ausgedrückt, beantwortet sie die Frage: "Was ist der Wert von x, bei dem die Cdf-Funktion die kumulative Wahrscheinlichkeit y zurückgibt?"
pdf oder die Wahrscheinlichkeitsdichtefunktion
Beschreibt die relative Wahrscheinlichkeit für eine zufällige Variable, um ein bestimmtes Wert zu sein.
Mit anderen Worten, es beantwortet die Frage: "Wie häufig sind Beispiele genau diesen Wert?"
Erwartete Eingaben
| Name | type | BESCHREIBUNG |
|---|---|---|
| Dataset | Datentabelle | Eingabedataset |
Modulparameter
| Name | Range | type | Standard | BESCHREIBUNG |
|---|---|---|---|---|
| Distribution | Any | ProbabilityDistribution | StandardNormal | Wählen Sie die Art der zu generierenden Wahrscheinlichkeitsverteilung aus. |
| Methode | Any | ProbabilityDistributionMethod | Cdf | Wählen Sie die Methode aus, die beim Berechnen der ausgewählten Wahrscheinlichkeitsverteilung verwendet werden soll. Die Optionen sind die kumulative Verteilungsfunktion (cdf), die inverse kumulative Verteilungsfunktion (InverseCdf) und die Wahrscheinlichkeitsdichte- oder Wahrscheinlichkeitsmassenfunktion (pdf). |
| Negative binomial distribution method | Any | ProbabilityDistributionMethodForNegativeBinomial | Cdf | Wenn Sie die negative Binomialverteilung auswählen, geben Sie die Methode an, die zum Auswerten der Verteilung verwendet wird. |
| Probability of success | [0.0;1.0] | Float | 0.5 | Geben Sie einen Wert ein, der als Erfolgswahrscheinlichkeit verwendet wird. |
| Form | Any | Float | 1,0 | Geben Sie einen Wert ein, der die Form der Verteilung ändert. |
| Skalieren | >=0.0 | Float | 1,0 | Geben Sie einen Wert ein, der die Skalierung der Verteilung ändert, sodass die Größe geändert werden kann. |
| Number of trials | >=1 | Integer | 3 | Geben Sie die Anzahl der Versuche an. |
| Unterer Grenzwert | Any | Float | 0,0 | Geben Sie eine Zahl ein, die als die untere Grenze der Verteilung verwendet wird. |
| Upper bound | Any | Float | 1.0 | Geben Sie eine Zahl ein, die als die obere Grenze der Verteilung verwendet wird. |
| Standort | Any | Float | 0,0 | Geben Sie die Position des Nullelements in der Verteilung ein. |
| Number of degrees of freedom | Any | Float | 1,0 | Geben Sie die Anzahl der Freiheitsgrade an. |
| Numerator degrees of freedom | Any | Float | 3.0 | Geben Sie die Anzahl der Freiheitsgrade im Zähler an. |
| Denominator degrees of freedom | Any | Float | 6.0 | Geben Sie die Anzahl der Freiheitsgrade im Nenner an. |
| Lambda | >=0.0 | Float | 1,0 | Geben Sie einen Wert für den Lambda-Parameter an. |
| Anzahl der Stichproben | Any | Integer | 9 | Geben Sie die Anzahl der Stichproben an. |
| Number of success | Any | Integer | 24 | Geben Sie einen Wert ein, der als die Anzahl der Erfolge verwendet wird. |
| Population size | Any | Integer | 52 | Geben Sie die Größe der Grundgesamtheit an. |
| Mittelwert | Any | Float | 0,0 | Geben Sie den geschätzten Mittelwert ein. |
| Standardabweichung | >=0,0 | Float | 1.0 | Geben Sie die geschätzte Standardabweichung ein. |
| Spaltensatz | Any | ColumnSelection | Wählen Sie die Spalten aus, für die die Wahrscheinlichkeitsverteilung berechnet werden soll. | |
| Result mode | Any | OutputTo | ResultOnly | Geben Sie an, wie die Ergebnisse im Ausgabedataset gespeichert werden sollen. Optional können neue Spalten angefügt, vorhandene Spalten ersetzt oder nur die Ergebnisse ausgegeben werden. |
Output
| Name | type | BESCHREIBUNG |
|---|---|---|
| Ergebnisdataset | Datentabelle | Ausgabedataset |
Ausnahme
Eine vollständige Liste der Fehlermeldungen finden Sie unter Modulfehlercodes.
| Ausnahme | Beschreibung |
|---|---|
| Fehler 0017 | Eine Ausnahme tritt auf, wenn mindestens eine der angegebenen Spalten einen Typ aufweist, der vom aktuellen Modul nicht unterstützt wird. |
Eine Liste der Fehler, die für Studio-Module (klassische) spezifisch sind, finden Sie unter Machine Learning Fehlercodes.
Eine Liste der API-Ausnahmen finden Sie unter Machine Learning REST-API-Fehlercodes.