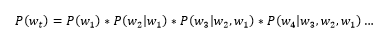Méthodes probabilistes en Machine Learning
Dans l’introduction à l’apprentissage automatique ((#MachineLearning ou ML) que nous avons souhaitée partager avec vous avec ce nouveau blog, nous avons détaillé plusieurs méthodes d’apprentissage supervisé et non-supervisé au travers de quels billets. Ainsi, en première approche pour entrer de façon pragmatique dans le monde du Machine Learning, il nous a paru intéressant de détailler quelques-uns des algorithmes les plus courants.
Au-delà de ces algorithmes pour illustrer les principes de base, il existe de nombreux algorithmes également très utilisés mais certes un peu plus complexes. Abordons-en quelques-uns !
Régression logistique
Utiliser les méthodes de régression pour la classification
On parle de régression lorsqu’on cherche à prédire un attribut continu, c’est-à-dire le nombre de valeurs que l’attribut à prédire peut prendre est infini. Le type de régression le plus connu et le plus utilisé est la régression linéaire. D’un autre côté, lorsque l’attribut à prédire est discret, on parle de classification.
Contrairement à ce que l’on pourrait penser, la régression logistique est une méthode de classification, au détail près qu’elle procède à une régression sur des attributs discrets. L’avantage est qu’en plus de renvoyer l’attribut prédit, l’algorithme renvoie un indicateur de confiance relatif à la prédiction.
Principe de fonctionnement
Supposons que l’on souhaite effectuer une classification binaire à l’aide d’une régression logistique. Les valeurs à prédire peuvent donc être notées 0 et 1. Etant donné un échantillon, plutôt que de renvoyer une classe 0 ou 1, la régression logistique renvoie un résultat entre 0 et 1 décrivant la probabilité d’appartenance à la classe 1 dont on peut déduire facilement la probabilité d’appartenance à la classe 0 ;)
Afin d’approximer le résultat, on utilise une famille de fonctions particulières dont les valeurs sont toujours comprises entre 0 et 1 appelée la famille des fonctions logistiques.
Effectuer l’entraînement consiste à trouver le paramètre r de la fonction logistique.
En général, r est calculé par essais itératifs de sorte à maximiser la vraisemblance avec une méthode du gradient. Pour plus d’informations sur la régression logistique, notamment l’estimation des paramètres, vous pouvez vous référer au billet sur la régression.
Réseaux neuronaux
Un réseau neuronal est un algorithme complexe, prédécesseur des réseaux profonds ou Deep Learning connus pour être les plus innovants aujourd’hui. Les réseaux neuronaux sont appelés ainsi par analogie avec le fonctionnement du cerveau humain.
La brique de base : le neurone
Des études en neurologie montrent que chaque neurone du cerveau se comporte comme une fonction seuil : un potentiel d’action n’est renvoyé qu’à partir d’une certaine valeur des entrées. Pour des soucis d’optimisation, on remplace cette fonction seuil par une fonction sigmoïde (facilement dérivable).
Assembler des neurones
En combinant plusieurs neurones aussi appelés perceptrons (représentés par des ronds bleus remplis d’une sigmoïde), on peut obtenir un réseau neuronal.
L’entrée de chaque neurone est une combinaison linéaire des sorties précédentes. Entraîner le réseau consiste à déterminer les poids de chaque combinaison linéaire. En particulier, nous verrons qu’un réseau neuronal procède à plusieurs régressions logistiques en même temps ! :)
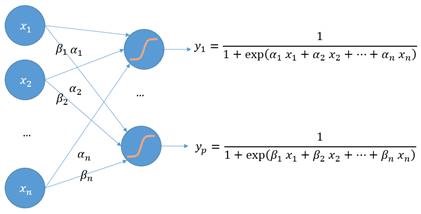
Prenons l’exemple d’un réseau de neurones prenant en entrée un vecteur x = (x1, x2, …, xn) et renvoyant en sortie une décision y.
Dans ce cas de réseau neuronal simple, une régression logistique est réalisée sur une combinaison linéaire des entrées (autre représentation des entrées).
Entraîner le réseau neuronal consiste à déterminer les coefficients 
Dans le cadre de ce billet nous ne détaillerons pas cette étape.
Possibilités des réseaux neuronaux
Essayons maintenant d’ajouter des neurones à notre réseau de sorte d’avoir p neurones sur la seconde couche :
Arrêtons-nous quelques instants sur ce schéma. Nous voyons que le vecteur y = (y1, y2, …, yp) est une représentation différente du vecteur d’entrée x. Si p < n, y est une version compressée de x, si p > n, y est la projection de x sur un espace de plus grande dimension. Autrement dit y s’obtient par l’application d’une fonction noyau particulière sur x.
Les réseaux neuronaux ont donc les mêmes possibilités que les méthodes à noyau, c’est-à-dire qu’avec un réseau neuronal à une couche, il est possible de modéliser n’importe quelle fonction (sous condition qu’il y ait assez de neurones).
Une initiation au Deep Learning
Une autre vision des choses est de considérer qu’apprendre les coefficients du réseau neuronal revient à faire une extraction de caractéristiques (feature selection) de manière automatique sur les entrées. Et comme chaque couche du réseau neuronal est une représentation de plus haut niveau des entrées, superposer les couches permet d’avoir une représentation d’un niveau d’abstraction encore plus haut des entrées.
Une décision peut être prise en ajoutant une couche à un seul neurone, ce qui a pour effet de combiner l’effet de chaque composante de la dernière représentation des entrées.
Les couches intermédiaires entre les entrées et le résultat sont appelées couches cachées.
Augmenter le nombre de couches à nombre de neurones constants permet donc de représenter des fonctions plus complexes en utilisant moins de neurones.
Petite digression additionnelle : une analyse en composantes principales avec des réseaux neuronaux
Nous venons de voir que les possibilités des réseaux neuronaux étaient les mêmes que les méthodes classiques de Machine Learning : il est possible d’approximer n’importe quelle fonction.
En particulier, on peut écrire une version améliorée de l’analyse en composantes principales avec un réseau neuronal à une couche cachée.
Les possibilités des réseaux neuronaux étant à présent couverte, continuons notre « exploration » des algorithmes plus complexes.
Modèles de Markov
Les modèles de Markov sont des modèles de Machine Learning très utilisés lorsqu’on souhaite prédire des séquences d’événements. Par exemple, ces modèles sont utilisés comme modèles de prédiction du langage pour améliorer la traduction automatique.
Quelques exemples pour illustrer le propos
On souhaite modéliser un texte en utilisant les probabilités de passage d’un mot à l’autre. Pour cela, on modélise chaque mot par un rond que l’on va appeler état.
Nous disposons d’un corpus de texte, par exemple des articles de journaux d’actualité.
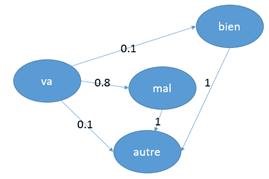
Voici comment nous souhaitons modéliser ce texte à l’aide de chaînes de Markov :
Dans notre corpus d’entraînement, le mot va était suivi dans 10% des cas du mot bien, dans 80% des cas du mot mal et dans 10% des cas d’un autre mot.
Supposons donc que l’on rencontre le mot va, la probabilité que le mot suivant soit bien est de 10%, la probabilité que le mot suivant soit mal est de 80% et la probabilité que le mot suivant soit un autre mot est de 10%.
Conclusion : en général, la presse communique plus quand tout va mal plutôt que quand tout va bien ! ;)
Prenons maintenant le cas suivant :
Cette modélisation ne permet pas de savoir si la France va mieux que l’Allemagne. Nous restons dans l’actualité et le quotidien de la presse…
Pour prendre en compte ce phénomène, on utilise une approximation de Markov d’ordre 2 : la probabilité de passage à l’état courant dépend de l’état précédent ET de l’état anté-précédent. Par exemple, dans le modèle précédent, les probabilités de bien, mal, et autre dépendaient uniquement du fait de se trouver sur le mot va. Le nouveau modèle tient compte des états France suivi de va (ou de Allemagne suivi de va) pour prendre une décision.
Pour cela, on peut également opter pour un modèle de Markov d’ordre 1 en considérant non plus les mots mais les bi-grammes. Vous pouvez vous référer à un ancien billet publié sur le blog MSDN Big Data France pour plus d’informations.
Formalisation appliquée à la création d’un modèle statistique du langage
La probabilité d’apparition d’un mot dépend de tous les mots qui lui ont précédé :
Une approximation de Markov d’ordre 1 donnerait :
Pour entraîner un modèle de Markov d’ordre 1, c’est-à-dire trouver les coefficients entre les états, il faut compter le nombre de passage entre les différents états puis normaliser afin d’obtenir une probabilité entre 0 et 1. Cette réflexion pour déterminer les coefficients d’entraînement provient de l’application du théorème de Bayes et place donc les modèles de Markov dans les modèles Bayésiens.
En guise de (rapide) conclusion
Ce billet nous a permis d’étendre les principes précédemment abordés et de partager dans ce contexte un premier regard sur un ensemble d’algorithmes plus complexes qu’il s’agisse de la régression logistique, des réseaux neuronaux, des modèles de Markov, ou encore des modèles Bayésiens qui est notre « ouverture » pour cette rapide conclusion.
D’une façon générale, ces algorithmes sont basés sur la théorie des probabilités : « l'étude mathématique des phénomènes caractérisés par le hasard et l'incertitude »
Tout cela renvoie à de très nombreuses lois (Loi de Bernoulli, Loi de Poisson, Loi uniforme, Loi normale, Loi de Student, Loi de Fisher) : un vaste champ d’investigation qui dépasse bien évidemment le cadre de ce billet :(
Notre objectif était plus limité ici. Il s’agissait de « pointer du doigt » que comprendre ces algorithmes permettait de passer outre la distinction que nous avions faite entre classification et régression.
Nous espérons qu’à ce titre ce billet vous aura apporté un éclairage complémentaire sur les principes mises en œuvre avec le Machine Learning.