Un peu de théorie pour l’apprentissage supervisé - 2nde partie

De façon à rentrer de plein pied dans le monde du Machine Learning, nous souhaitons partager une compréhension commune des principes de l’apprentissage automatique, et expliquer au travers d’une série courte de billet ce qu’est l’apprentissage supervisé et non-supervisé avec des applications ainsi que les moyens d’évaluer un modèle en apprentissage automatique.

Ce billet est pour l’essentiel une republication sur ce blog du billet éponyme déjà publié sur le blog Big Data France .

Je vous souhaite une bonne lecture de ce billet

--Philippe

_________________________________________________________________________________________

Après un regard sur l’apprentissage non-supervisé dans de précédents billets, la première partie de billet sur l’apprentissage supervisé s’est intéressée à la classification. Comme annoncé dans ce cadre, nous vous proposons à présent de détailler dans cette seconde partie quelques méthodes de régression.

Nous rappelons qu’il est question de régression en apprentissage supervisé lorsque l’attribut à prédire est continu.

Nous profitons de ce billet pour formaliser un peu plus notre vision de l’apprentissage supervisé à travers l’introduction de notions mathématiques supplémentaires et une brève introduction aux méthodes d’optimisation.

Une vision formalisée de l’apprentissage supervisé

Rappels d’algèbre

Une fonction f, ou modèle comme nous l’avons appelé précédemment, est un mécanisme qui transforme une donnée d’entrée x en un résultat y.

Une fonction est caractérisée par une équation du type :

Si une donnée x est constituée d’une composante ou dimension, on parle de scalaire ; si elle est constituée de plusieurs composantes comme suit :

, elle est alors appelée vecteur.

L’ensemble de tous les vecteurs x qu’il est possible de construire est appelé espace. Dans un espace, il existe au moins un sous-ensemble de vecteurs que l’on peut combiner par addition ou multiplication pour obtenir tout l’espace ; ce sous-ensemble de vecteurs est appelé base.

La matrice est la généralisation de la notion de vecteur : c’est un vecteur de vecteurs ou tableau à 2 dimensions. Il est possible d’additionner et multiplier des matrices entre elles, des vecteurs entre eux, et des matrices avec des vecteurs. Les matrices sont extrêmement utiles d’un point de vue notation, car elles permettent d’écrire de manière dense des équations de fonctions !

Enfin, on peut définir la norme d’un vecteur x  comme étant la distance de ce vecteur à l’origine. Cette dernière est notée comme suit :

On distingue en particulier :

• La norme 2 ou distance euclidienne :

• La norme 1 ou valeur absolue :

La notion de norme est également généralisable aux matrices, ce que nous ne détaillons pas ici.

Interpolation

Etant donné un historique de points, interpoler signifie déterminer la fonction qui passe par tous ces points. En général, on utilise une interpolation polynomiale (plus de détail ici). Cela pourrait constituer une méthode de régression, toutefois, on évite cette méthode car elle induit très souvent du sur-apprentissage.

Apprentissage supervisé avec des équations

Pour évaluer la performance d’un classifieur f, on définit d’abord une fonction de coût L qui va donner une mesure de l’erreur entre la prédiction f(x) et la valeur réelle y.

En général, la fonction de coût est choisie comme le carré de l’écart au résultat à prédire, c’est l’approximation des moindres carrés :

Ensuite, on définit une fonction erreur R qui mesure la somme des écarts entre la valeur réelle y et la prédiction f(x) .

où n est le nombre d’éléments dans l’historique

Alors, effectuer une régression consiste à trouver la fonction f qui minimise l’erreur :

Comment trouver le minimum d’une fonction ?

Il est important de préciser que f est une fonction dont la forme est connue (par exemple, une fonction linéaire du type y = a * x +b). Pour déterminer f, il suffit de déterminer ses paramètres. (Dans le cas de la fonction linéaire, les paramètres sont a et b). Ces paramètres s’obtiennent en minimisant la fonction erreur R.

Dans la plupart des cas, il existe des méthodes exactes pour minimiser R utilisant des opérations de calcul très coûteuses pour une machine. En général, il est plus rapide d’estimer la valeur des paramètres de f en effectuant plusieurs essais sur la valeur des paramètres. Le nombre de valeurs prises par les paramètres étant infini, il faut effectuer ces essais astucieusement. Pour cela, on fait appel à des méthodes d’optimisation, la plus connue étant la méthode du gradient.

Régression linéaire

Régression simple - x est un scalaire

La régression linéaire (plus de détail ici) est une méthode d’apprentissage supervisé permettant d’estimer f en supposant que f a une forme linéaire :

Déterminer f consiste alors à trouver a et b en minimisant la fonction R :

Comme expliqué précédemment, il est possible de résoudre cette équation à l’aide de la méthode du gradient.

Régression multiple - x est un vecteur

Dans ce cas,

où A est un vecteur et B un scalaire.

La formule d’optimisation devient :

Ainsi, avec les notations vectorielles, on constate qu’il est facile de généraliser la plupart des méthodes appliquées à des scalaires. Toutefois, le temps de calcul est plus important car il y a plus de coefficients à évaluer (p+1 coefficients au lieu de 2).

Régression multiple, notation matricielle

Dans la littérature, on trouve souvent ces équations posées sous forme matricielle afin d’avoir une écriture condensée.

Posons X la matrice constituée des n vecteurs x, Y la matrice constituée des n vecteurs y. Alors A devient une matrice et on peut écrire :

Une petite parenthèse sur les possibilités des régressions

Régressions non linéaires

Il existe de nombreux modèles de régression plus complexes que la régression linéaire, il faut choisir le bon type de régression pour le bon problème : régression polynomiale, splines, séries temporelles, régression logistique, régression à noyau…

Réduction de dimensions

Comme avec l’ACP en apprentissage non-supervisé, il est possible d’utiliser les méthodes de régression pour la réduction de dimensions.

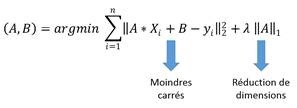
Lorsque le nombre de caractéristiques est grand, il est intéressant de déterminer quelles caractéristiques ont une influence sur le résultat. Pour cela, on utilise des méthodes de régularisation. Le principe de la régularisation est de corriger l’erreur R par un terme dépendant des paramètres valant 1 ou 0. Une des méthodes de régularisation s’appelle la régression Lasso :

Cette méthode permet de réduire le nombre de dimensions en annulant une grande partie des coefficients de A. Il convient de noter que le paramètre est à déterminer de manière empirique…

Nous en avons fini avec notre explication sur les régressions et ce billet sur l’apprentissage supervisé. Nous espérons vous avoir donné les bases pour en comprendre les principes et en apprendre plus par vous-mêmes :)