Neafinní transformace
Vytvoření perspektivy a zužovacího efektu pomocí třetího sloupce matice transformace
Překlad, škálování, otočení a skewing jsou všechny klasifikovány jako affinové transformace. Transformace Affine zachovávají paralelní čáry. Pokud jsou před transformací dva řádky paralelní, zůstanou po transformaci paralelně. Obdélníky se vždy transformují na paralelogramy.
SkiaSharp je však také schopen nefínových transformací, které mají schopnost transformovat obdélník na jakýkoli konvexní čtyřúhelník:

Konvexní čtyřúhelník je čtyřstranná postava s vnitřními úhly vždy menší než 180 stupňů a stran, které se navzájem neprotínají.
Pokud je třetí řádek matice transformace nastavený na jiné hodnoty než 0, 0 a 1, výsledkem je neffine. Úplné SKMatrix násobení je:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z' |
│ TransX TransY Persp2 │
Výsledné vzorce transformace jsou:
x' = ScaleX·x + SkewX·y + TransX
y' = Zkosený x + ScaleY·y + TransY
z' = Persp0·x + Persp1·y + Persp2
Základním pravidlem použití matice 3 by-3 pro dvojrozměrné transformace je, že vše zůstává na rovině, kde se Z rovná 1. Pokud Persp0 a Persp1 nejsou 0 a Persp2 rovná se 1, transformace přesunula souřadnice Z z této roviny.
Chcete-li tuto transformaci obnovit do dvourozměrné transformace, musí být souřadnice přesunuty zpět do této roviny. Je vyžadován další krok. Hodnoty x', y a z musí být rozděleny z':
x" = x' / z'
y" = y' / z'
z" = z' / z' = 1
Tyto souřadnice jsou známé jako homogenní souřadnice a byly vyvinuty matematikem Augustem Bernardem Möbiusem, mnohem lépe známým pro jeho topologickou lichost, Möbius Strip.
Pokud je z' 0, výsledkem dělení jsou nekonečné souřadnice. Ve skutečnosti byla jednou z motivací Möbius pro vývoj homogenních souřadnic schopnost reprezentovat nekonečné hodnoty s konečnými čísly.
Při zobrazení grafiky se ale chcete vyhnout vykreslení něčeho s souřadnicemi, které transformují na nekonečné hodnoty. Tyto souřadnice se nevykreslí. Vše v blízkosti těchto souřadnic bude velmi velké a pravděpodobně není vizuálně koherentní.
V této rovnici nechcete, aby se hodnota z stala nulou:
z' = Persp0·x + Persp1·y + Persp2
V důsledku toho mají tyto hodnoty určitá praktická omezení:
Buňka Persp2 může být buď nula, nebo ne nula. Pokud Persp2 je nula, pak z' je nula pro bod (0, 0), a to obvykle není žádoucí, protože tento bod je velmi společný v dvojrozměrné grafiky. Pokud Persp2 se nerovná nule, pak nedojde ke ztrátě generality, pokud Persp2 je pevná hodnota 1. Pokud například zjistíte, že Persp2 by mělo být 5, můžete jednoduše vydělit všechny buňky v matici 5, což se rovná Persp2 1 a výsledek bude stejný.
Z těchto důvodů Persp2 je často pevně nastavená hodnota 1, což je stejná hodnota v matici identit.
Obecně platí, že Persp0 jde Persp1 o malá čísla. Předpokládejme například, že začínáte maticí identity, ale nastavíte Persp0 ji na 0,01:
| 1 0 0.01 | | 0 1 0 | | 0 0 1 |
Vzorce transformace jsou:
x' = x / (0,01·x + 1)
y' = y / (0,01·x + 1)
Teď tuto transformaci použijte k vykreslení čtvercového rámečku o rozměrech 100 pixelů umístěného na počátku. Čtyři rohy se transformují takto:
(0, 0) → (0, 0)
(0, 100) → (0, 100)
(100, 0) → (50, 0)
(100, 100) → (50, 50)
Když je x 100, pak jmenovatel z' je 2, takže souřadnice x a y jsou efektivně halvovány. Pravá strana rámečku se zkrátí než levá strana:
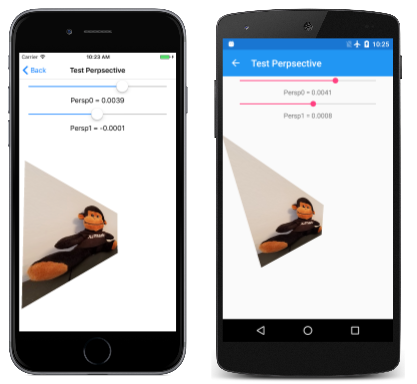
Část Persp těchto názvů buněk odkazuje na "perspektivu", protože eshortening naznačuje, že pole je nyní nakloněno pravou stranou dále od prohlížeče.
Stránka Perspektiva testu umožňuje experimentovat s hodnotami Persp0 a Pers1 získat pocit, jak fungují. Rozumné hodnoty těchto maticových buněk jsou tak malé, že Slider je v Univerzální platforma Windows nedokáže správně zpracovat. Aby bylo možné problém s UPW vyřešit, musí být dva Slider prvky v souboru TestPerspective.xaml inicializovány tak, aby byly v rozsahu od –1 do 1:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.TestPerspectivePage"
Title="Test Perpsective">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Minimum" Value="-1" />
<Setter Property="Maximum" Value="1" />
<Setter Property="Margin" Value="20, 0" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="persp0Slider"
Grid.Row="0"
ValueChanged="OnPersp0SliderValueChanged" />
<Label x:Name="persp0Label"
Text="Persp0 = 0.0000"
Grid.Row="1" />
<Slider x:Name="persp1Slider"
Grid.Row="2"
ValueChanged="OnPersp1SliderValueChanged" />
<Label x:Name="persp1Label"
Text="Persp1 = 0.0000"
Grid.Row="3" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="4"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Obslužné rutiny událostí pro posuvníky v TestPerspectivePage souboru kódu zadělují hodnoty hodnotou 100 tak, aby byly v rozsahu od –0,01 do 0,01. Konstruktor se navíc načte v rastrovém obrázku:
public partial class TestPerspectivePage : ContentPage
{
SKBitmap bitmap;
public TestPerspectivePage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnPersp0SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp0Label.Text = String.Format("Persp0 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
void OnPersp1SliderValueChanged(object sender, ValueChangedEventArgs args)
{
Slider slider = (Slider)sender;
persp1Label.Text = String.Format("Persp1 = {0:F4}", slider.Value / 100);
canvasView.InvalidateSurface();
}
...
}
Obslužná PaintSurface rutina vypočítá hodnotu pojmenovanou perspectiveMatrix SKMatrix na základě hodnot těchto dvou posuvníků rozdělených hodnotou 100. To je kombinováno se dvěma transformacemi, které umístí střed této transformace do středu rastrového obrázku:
public partial class TestPerspectivePage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Calculate perspective matrix
SKMatrix perspectiveMatrix = SKMatrix.MakeIdentity();
perspectiveMatrix.Persp0 = (float)persp0Slider.Value / 100;
perspectiveMatrix.Persp1 = (float)persp1Slider.Value / 100;
// Center of screen
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
SKMatrix.PostConcat(ref matrix, perspectiveMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(xCenter, yCenter));
// Coordinates to center bitmap on canvas
float x = xCenter - bitmap.Width / 2;
float y = yCenter - bitmap.Height / 2;
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
}
Tady je několik ukázkových obrázků:
Při experimentování s posuvníky zjistíte, že hodnoty nad 0,0066 nebo nižší –0,0066 způsobí, že obrázek se náhle zlomí a inkoherentní. Transformovaný rastrový obrázek je čtvercový 300 pixelů. Transformuje se vzhledem ke středu, takže souřadnice rastrového obrázku od –150 do 150. Vzpomeňte si, že hodnota z' je:
z' = Persp0·x + Persp1·y + 1
Pokud Persp0 je nebo Persp1 je větší než 0,0066 nebo nižší –0,0066, existuje vždy nějaká souřadnice rastrového obrázku, která vede k hodnotě z' nuly. To způsobí dělení nulou a vykreslování se stane nepořádkem. Pokud používáte jiné než affinové transformace, chcete se vyhnout vykreslení čehokoli se souřadnicemi, které způsobují dělení nulou.
Obecně platí, že nebudete nastavení Persp0 a Persp1 izolace. Často je také nutné nastavit další buňky v matici, aby bylo možné dosáhnout určitých typů neffinových transformací.
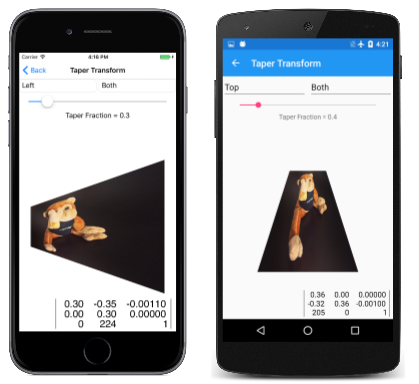
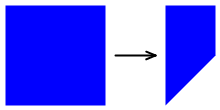
Jednou z takových neffinových transformací je klepací transformace. Tento typ neffinové transformace zachovává celkové rozměry obdélníku, ale klepá na jednu stranu:
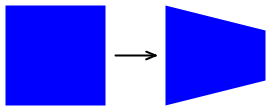
Třída TaperTransform provádí zobecněný výpočet transformace bez affinu na základě těchto parametrů:
- obdélníková velikost transformovaného obrázku,
- výčet, který označuje stranu obdélníku, který klepá,
- další výčet, který indikuje, jak klepá, a
- rozsah zkosení.
Tady je kód:
enum TaperSide { Left, Top, Right, Bottom }
enum TaperCorner { LeftOrTop, RightOrBottom, Both }
static class TaperTransform
{
public static SKMatrix Make(SKSize size, TaperSide taperSide, TaperCorner taperCorner, float taperFraction)
{
SKMatrix matrix = SKMatrix.MakeIdentity();
switch (taperSide)
{
case TaperSide.Left:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp0 = (taperFraction - 1) / size.Width;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
matrix.TransY = size.Height * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Top:
matrix.ScaleX = taperFraction;
matrix.ScaleY = taperFraction;
matrix.Persp1 = (taperFraction - 1) / size.Height;
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction);
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
matrix.TransX = size.Width * (1 - taperFraction) / 2;
break;
}
break;
case TaperSide.Right:
matrix.ScaleX = 1 / taperFraction;
matrix.Persp0 = (1 - taperFraction) / (size.Width * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewY = size.Height * matrix.Persp0;
break;
case TaperCorner.Both:
matrix.SkewY = (size.Height / 2) * matrix.Persp0;
break;
}
break;
case TaperSide.Bottom:
matrix.ScaleY = 1 / taperFraction;
matrix.Persp1 = (1 - taperFraction) / (size.Height * taperFraction);
switch (taperCorner)
{
case TaperCorner.RightOrBottom:
break;
case TaperCorner.LeftOrTop:
matrix.SkewX = size.Width * matrix.Persp1;
break;
case TaperCorner.Both:
matrix.SkewX = (size.Width / 2) * matrix.Persp1;
break;
}
break;
}
return matrix;
}
}
Tato třída se používá na stránce Transformace taperu . Soubor XAML vytvoří instanci dvou Picker prvků pro výběr hodnot výčtu a výběr Slider zlomku zvětšování. Obslužná rutina PaintSurface kombinuje klepací transformaci se dvěma transformacemi překladu, aby byla transformace relativní k levému hornímu rohu rastrového obrázku:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
TaperSide taperSide = (TaperSide)taperSidePicker.SelectedItem;
TaperCorner taperCorner = (TaperCorner)taperCornerPicker.SelectedItem;
float taperFraction = (float)taperFractionSlider.Value;
SKMatrix taperMatrix =
TaperTransform.Make(new SKSize(bitmap.Width, bitmap.Height),
taperSide, taperCorner, taperFraction);
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(taperMatrix);
matrixDisplay.Paint(canvas, taperMatrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Center bitmap on canvas
float x = (info.Width - bitmap.Width) / 2;
float y = (info.Height - bitmap.Height) / 2;
SKMatrix matrix = SKMatrix.MakeTranslation(-x, -y);
SKMatrix.PostConcat(ref matrix, taperMatrix);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(x, y));
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, x, y);
}
Několik příkladů:
Dalším typem generalizovaných neffinových transformací je 3D otočení, které je znázorněno v dalším článku 3D otočení.
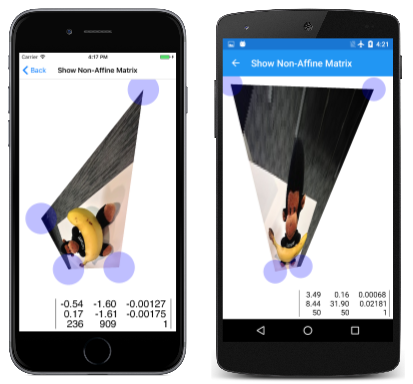
Transformace bez affinu může transformovat obdélník na jakýkoli konvexní čtyřúhelník. To ukazuje stránka Zobrazit nefakfinovou matici . Je velmi podobný stránce Zobrazit matici Affine z článku Transformace matice s tím rozdílem, že má čtvrtý TouchPoint objekt pro manipulaci se čtvrtým rohem rastrového obrázku:
Pokud se nepokoušíte vytvořit vnitřní úhel jednoho z rohů rastrového obrázku větší než 180 stupňů, nebo aby se dvě strany navzájem přeškrtly, program úspěšně vypočítá transformaci pomocí této metody z ShowNonAffineMatrixPage třídy:
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL, SKPoint ptLR)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
// Non-Affine transform
SKMatrix inverseA;
A.TryInvert(out inverseA);
SKPoint abPoint = inverseA.MapPoint(ptLR);
float a = abPoint.X;
float b = abPoint.Y;
float scaleX = a / (a + b - 1);
float scaleY = b / (a + b - 1);
SKMatrix N = new SKMatrix
{
ScaleX = scaleX,
ScaleY = scaleY,
Persp0 = scaleX - 1,
Persp1 = scaleY - 1,
Persp2 = 1
};
// Multiply S * N * A
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.PostConcat(ref result, S);
SKMatrix.PostConcat(ref result, N);
SKMatrix.PostConcat(ref result, A);
return result;
}
Pro usnadnění výpočtu tato metoda získá celkovou transformaci jako součin tří samostatných transformací, které jsou zde symbolizovány pomocí šipek ukazujících, jak tyto transformace upravují čtyři rohy rastrového obrázku:
(0, 0) → (0, 0) → (0, 0) → (x0, y0) (vlevo nahoře)
(0, H) → (0, 1) → (0, 1) → (x1, y1) (vlevo dole)
(W, 0) → (1, 0) → (1, 0) → (x2, y2) (vpravo nahoře)
(W, H) → (1, 1) → (a, b) → (x3, y3) (vpravo dole)
Konečné souřadnice vpravo jsou čtyři body spojené se čtyřmi dotykovými body. Jedná se o konečné souřadnice rohů rastrového obrázku.
W a H představují šířku a výšku rastrového obrázku. První transformace S jednoduše škáluje rastrový obrázek na 1 pixelový čtverec. Druhá transformace je neffinová transformace Na třetí je afinní transformace A. Tato affinová transformace je založená na třech bodech, takže je to stejně jako předchozí metoda affine ComputeMatrix a nezahrnuje čtvrtý řádek s bodem (a, b).
Hodnoty a a b hodnoty se počítají tak, aby třetí transformace byla affine. Kód získá inverzní funkci k affinové transformaci a pak ho použije k namapování pravého dolního rohu. To je ten bod (a, b).
Dalším použitím neffinových transformací je napodobování trojrozměrné grafiky. V dalším článku 3D otočení uvidíte, jak otočit dvojrozměrnou grafiku v prostorovém prostoru.