3D otočení v skiaSharpu
K otočení 2D objektů ve 3D prostoru použijte nefínové transformace.
Jednou z běžných aplikací neffinových transformací je simulace otočení 2D objektu v 3D prostoru:
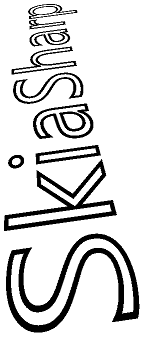
Tato úloha zahrnuje práci s trojrozměrnými rotacemi a následným odvozením neffinové SKMatrix transformace, která provádí tyto 3D otočení.
Tento transformační postup je těžké vyvinout SKMatrix výhradně ve dvou dimenzích. Úloha je mnohem jednodušší, když je tato matice 3 po 3 odvozena od matice 4 po 4 použité v 3D grafikách. SkiaSharp zahrnuje SKMatrix44 třídu pro tento účel, ale některé pozadí 3D grafiky je nezbytné pro pochopení 3D otočení a transformační matice 4 po 4.
Trojrozměrný souřadnicový systém přidá třetí osu s názvem Z. Koncepčně je osa Z v pravých úhlech na obrazovku. Souřadnicové body v 3D prostoru jsou označené třemi čísly: (x, y, z). V 3D souřadnicovém systému použitém v tomto článku jsou zvýšení hodnot X napravo a zvýšení hodnot Y dolů, stejně jako ve dvou dimenzích. Zvýšení kladných hodnot Z vychází z obrazovky. Původ je levý horní roh, stejně jako u 2D grafiky. Obrazovku si můžete představit jako rovinu XY s osou Z v pravých úhlech k této rovině.
Tomu se říká souřadnicový systém vlevo. Pokud nasměrujete forefinger pro levou ruku ve směru kladných souřadnic X (vpravo) a prostředním prstem směrem ke zvýšení souřadnic Y (dolů), pak palec ve směru zvýšení souřadnic Z – rozšiřuje se z obrazovky.
V 3D grafikě jsou transformace založeny na matici 4 po 4. Tady je matice identit 4 po 4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Při práci s maticí 4 po 4 je vhodné identifikovat buňky s čísly řádků a sloupců:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Třída SkiaSharp Matrix44 je ale trochu jiná. Jediným způsobem, jak nastavit nebo získat jednotlivé hodnoty SKMatrix44 buněk, je použití indexeru Item . Indexy řádků a sloupců jsou založené na nule než na jednom a řádky a sloupce se prohodí. K buňce M14 ve výše uvedeném diagramu se přistupuje pomocí indexeru [3, 0] v objektu SKMatrix44 .
V 3D grafickém systému se 3D bod (x, y, z) převede na 1:4 matici pro vynásobení transformační maticí 4:4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Podobně jako u 2D transformací, které probíhají ve třech dimenzích, se předpokládá, že se 3D transformace provádějí ve čtyřech dimenzích. Čtvrtá dimenze se označuje jako W a předpokládá se, že 3D prostor existuje ve 4D prostoru, kde souřadnice W jsou rovny 1. Vzorce transformace jsou následující:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Z transformačních vzorců je zřejmé, že buňky M11, M22jsou M33 faktory měřítka ve směrech X, Y a Z a M41, M42a M43 jsou faktory překladu ve směrech X, Y a Z.
Chcete-li tyto souřadnice převést zpět na prostor 3D, kde se W rovná 1, souřadnice x, y a z jsou všechny rozděleny pomocí w:
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Toto dělení w' poskytuje perspektivu v prostorech 3D. Pokud se rovná 1, nedojde k žádné perspektivě.
Otočení ve 3D prostoru mohou být poměrně složitá, ale nejjednodušší otočení jsou ty, které se nacházejí kolem os X, Y a Z. Otočení úhlu α kolem osy X je tato matice:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Hodnoty X zůstávají stejné, pokud jsou předmětem této transformace. Otočení kolem osy Y ponechá hodnoty Y beze změny:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
Otočení kolem osy Z je stejné jako u 2D grafiky:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Směr otáčení je odvozen předáním souřadnicového systému. Jedná se o levý systém, takže pokud nasměrujete palec levé ruky směrem ke zvýšení hodnot pro určitou osu – doprava pro otáčení kolem osy X, dolů pro otáčení kolem osy Y a směrem k vám pro otáčení kolem osy Z – pak křivka ostatních prstů označuje směr otáčení pro kladné úhly.
SKMatrix44 má generalizované statické CreateRotation a CreateRotationDegrees metody, které umožňují určit osu, kolem které se otočení vyskytuje:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Pokud chcete otočit osu X, nastavte první tři argumenty na 1, 0, 0. Pokud chcete otočit osu Y, nastavte je na 0, 1, 0 a pro otáčení kolem osy Z je nastavte na 0, 0, 1.
Čtvrtý sloupec 4 by-4 je určen pro perspektivu. Nemá SKMatrix44 žádné metody pro vytváření transformací perspektivy, ale můžete si ho vytvořit sami pomocí následujícího kódu:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
Důvod názvu depth argumentu bude zřejmě krátce. Tento kód vytvoří matici:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Výsledkem transformovaných vzorců je následující výpočet w':
w' = –z / depth + 1
Slouží ke snížení souřadnic X a Y, pokud jsou hodnoty Z menší než nula (koncepčně za rovinou XY) a ke zvýšení souřadnic X a Y pro kladné hodnoty Z. Když se souřadnice Z rovná depth, pak w' je nula a souřadnice se stanou nekonečnými. Třírozměrné grafické systémy jsou postaveny kolem metafory kamery a depth hodnota zde představuje vzdálenost kamery od původu souřadnicového systému. Pokud má grafický objekt souřadnici Z, která je depth jednotkami od počátku, je koncepčně dotknut objektiv fotoaparátu a stává se neomezeně velkým.
Mějte na paměti, že tuto perspectiveMatrix hodnotu budete pravděpodobně používat v kombinaci s maticemi otočení. Pokud otočený grafický objekt obsahuje souřadnice X nebo Y větší než depth, pak otočení tohoto objektu ve 3D prostoru pravděpodobně zahrnuje souřadnice Z větší než depth. Musí se tomu vyhnout! Při vytváření perspectiveMatrix chcete nastavit depth hodnotu dostatečně velkou pro všechny souřadnice v grafickém objektu bez ohledu na to, jak se otočí. Tím se zajistí, že nikdy nedojde k žádnému dělení nulou.
Kombinace 3D otočení a perspektivy vyžaduje vynásobení 4-4 matice dohromady. Pro tento účel SKMatrix44 definuje metody zřetězení. Pokud A a B jsou SKMatrix44 objekty, pak následující kód nastaví A rovná se A × B:
A.PostConcat(B);
Pokud se 4-by-4 transformační matice používá v 2D grafickém systému, použije se na 2D objekty. Tyto objekty jsou ploché a předpokládá se, že mají souřadnice Z nuly. Násobení transformace je o něco jednodušší než transformace zobrazená dříve:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Výsledkem této hodnoty 0 pro z jsou vzorce transformace, které neobsahují žádné buňky ve třetím řádku matice:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Souřadnice z je navíc tady irelevantní. Když se 3D objekt zobrazí v grafickém systému 2D, je sbalený do dvojrozměrného objektu ignorováním hodnot souřadnic Z. Transformační vzorce jsou ve skutečnosti jen tyto dvě:
x" = x' / w'
y" = y' / w'
To znamená, že třetí řádek a třetí sloupec matice 4 po 4 je možné ignorovat.
Ale pokud ano, proč je matice 4 by-4 dokonce nezbytná na prvním místě?
I když třetí řádek a třetí sloupec 4 po 4 jsou irelevantní pro dvojrozměrné transformace, třetí řádek a sloupec hrají roli před tím, když se různé SKMatrix44 hodnoty vynásobí dohromady. Předpokládejme například, že násobíte otočení kolem osy Y transformací perspektivy:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
V součinu teď buňka M14 obsahuje perspektivní hodnotu. Pokud chcete tuto matici použít u 2D objektů, třetí řádek a sloupec se eliminují, aby se převedly na 3 po 3 matici:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Teď ho můžete použít k transformaci 2D bodu:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Vzorce transformace jsou:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Teď vydělte všechno z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Když jsou 2D objekty otočeny kladným úhlem kolem osy Y, poté se kladné hodnoty X ustupují na pozadí, zatímco záporné hodnoty X přicházejí do popředí. Zdá se, že hodnoty X se pohybují blíž k ose Y (která se řídí kosinusovou hodnotou), protože souřadnice od osy Y se zmenší nebo zvětší, protože se pohybují dál od diváka nebo blíž k prohlížeči.
Při použití SKMatrix44proveďte všechny 3D operace otočení a perspektivy vynásobením různých SKMatrix44 hodnot. Pak můžete extrahovat dvojrozměrnou matici 3 po 3 z matice 4 po 4 pomocí Matrix vlastnosti SKMatrix44 třídy. Tato vlastnost vrátí známou SKMatrix hodnotu.
Stránka Otočení 3D umožňuje experimentovat s 3D otočením. Soubor Rotation3DPage.xaml vytvoří instanci čtyř posuvníků, které nastaví otočení kolem os X, Y a Z a nastaví hloubkovou hodnotu:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Všimněte si, že se depthSlider inicializuje s Minimum hodnotou 250. To znamená, že objekt 2D otočený zde má souřadnice X a Y omezené na kruh definovaný poloměrem 250 pixelů kolem původu. Jakékoli otočení tohoto objektu ve 3D prostoru vždy způsobí souřadnicové hodnoty menší než 250.
Soubor Rotation3DPage.cs za kódem se načte v rastrovém obrázku o rozměrech 300 pixelů:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Pokud je 3D transformace na střed na tomto rastrovém obrázku, pak souřadnice X a Y v rozsahu od –150 do 150, zatímco rohy jsou 212 pixelů od středu, takže vše je v okruhu 250 pixelů.
Obslužná rutina PaintSurface vytváří SKMatrix44 objekty na základě posuvníků a vynásobí je společně pomocí PostConcat. Hodnota SKMatrix extrahovaná z posledního SKMatrix44 objektu je obklopena transformacemi, které založí otočení na střed obrazovky:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Při experimentování se čtvrtým posuvníkem si všimnete, že různá nastavení hloubky nepřesunou objekt dál od prohlížeče, ale místo toho změní rozsah perspektivního efektu:
Animovaný otočení 3D také používá SKMatrix44 k animaci textového řetězce v 3D prostoru. Objekt textPaint nastavený jako pole se používá v konstruktoru k určení hranic textu:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Přepsání OnAppearing definuje tři Xamarin.FormsAnimation objekty, které se mají animovat xRotationDegrees, yRotationDegreesa zRotationDegrees pole s různými rychlostmi. Všimněte si, že období těchto animací jsou nastavená na počáteční čísla (5 sekund, 7 sekund a 11 sekund), takže se celková kombinace opakuje jenom každých 385 sekund nebo déle než 10 minut:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Stejně jako v předchozím programu obslužná rutina PaintCanvas vytvoří SKMatrix44 hodnoty pro otočení a perspektivu a vynásobí je dohromady:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Toto 3D otočení je obklopeno několika 2D transformacemi, které přesunou střed otáčení do středu obrazovky a velikost textového řetězce se zvětší tak, aby byla stejná šířka jako obrazovka: