Tři typy Bézierových křivek
Prozkoumejte, jak pomocí SkiaSharp vykreslit krychlové, kvadratické a kosnicové křivky Bézier
Bézierova křivka je pojmenována po Pierre Bézier (1910 – 1999), francouzský inženýr v automobilové společnosti Renault, který použil křivku pro počítačové navrhování aut.
Bézierovy křivky jsou známé za to, že jsou vhodné pro interaktivní návrh: Jsou dobře se chovají – jinými slovy, neexistují jedinečné hodnoty, které způsobují, že se křivka stane nekonečným nebo nepraktným – a obecně jsou esteticky příjemné:

Obrysy znaků počítačových písem jsou obvykle definovány pomocí Bézierových křivek.
Článek na Wikipedii o Bézierovy křivkě obsahuje některé užitečné informace o pozadí. Pojem Bézierova křivka ve skutečnosti odkazuje na řadu podobných křivek. SkiaSharp podporuje tři typy Bézierových křivek, označované jako krychlový, kvadratický a kuželový. Kužel je také známý jako logický kvadratický.
Krychlový Bézierův křivka
Krychlový je typ Bézierovy křivky, o které většina vývojářů uvažuje, když se objeví předmět Bézierových křivek.
K objektu SKPath můžete přidat krychlovou křivku Bézier pomocí CubicTo metody se třemi SKPoint parametry nebo CubicTo přetížení s oddělenými x parametry a y parametry:
public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)
public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)
Křivka začíná v aktuálním bodě obrysu. Úplná krychlová bezierová křivka je definována čtyřmi body:
- počáteční bod: aktuální bod v obrysu nebo (0, 0), pokud
MoveTonebyl volána - první řídicí bod:
point1veCubicTovolání - druhý řídicí bod:
point2veCubicTovolání - koncový bod:
point3vCubicTohovoru
Výsledná křivka začíná na začátku a končí na koncovém bodě. Křivka obecně neprojde dvěma kontrolními body; místo toho kontrolní body fungují podobně jako magnety, aby se k nim vytáhla křivka.
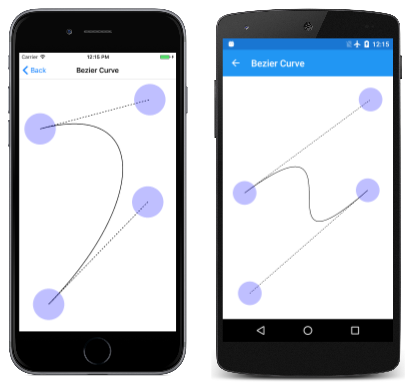
Nejlepší způsob, jak získat pocit krychlové Bézierovy křivky, je experimentování. Toto je účel stránky Bezier Curve , která je odvozena od InteractivePage. Soubor BezierCurvePage.xaml vytvoří SKCanvasView instanci a TouchEffect. Soubor BezierCurvePage.xaml.cs kódu vytvoří ve svém konstruktoru čtyři TouchPoint objekty. Obslužná rutina PaintSurface události vytvoří vykreslení SKPath Bézierovy křivky založené na čtyřech TouchPoint objektech a také nakreslí tečkované tečny z řídicích bodů na koncové body:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with cubic Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.CubicTo(touchPoints[1].Center,
touchPoints[2].Center,
touchPoints[3].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[2].Center.X,
touchPoints[2].Center.Y,
touchPoints[3].Center.X,
touchPoints[3].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Tady je spuštěný:
Matematicky je křivka krychlovým polynomem. Křivka protíná přímku na třech bodech maximálně. Na začátku je křivka vždy tangens na a ve stejném směru jako přímka od počátečního bodu k prvnímu řídicímu bodu. Na konci je křivka vždy tangens na a ve stejném směru jako přímka od druhého kontrolního bodu do koncového bodu.
Krychlová křivka Bézier je vždy ohraničena konvexním čtyřúhelníkem spojujícím čtyři body. Tomu se říká konvexní trupu. Pokud kontrolní body leží na rovné přímce mezi počátečním a koncovým bodem, pak se křivka Bézier zobrazí jako přímka. Křivka se ale může také protíná, jak ukazuje třetí snímek obrazovky.
Obrys cesty může obsahovat více propojených krychlových Bézierových křivek, ale spojení mezi dvěma krychlovými Bézierovými křivkami bude hladké pouze v případě, že následující tři body jsou kolineární (to znamená leží na rovné přímce):
- druhý řídicí bod první křivky
- koncový bod první křivky, což je také počáteční bod druhé křivky
- první řídicí bod druhé křivky
V dalším článku o datech cesty SVG zjistíte zařízení, které usnadňuje definici hladkých propojených Bézierových křivek.
Někdy je užitečné znát základní parametrické rovnice, které vykreslují krychlovou Bézierovou křivku. V rozsahu od 0 do 1 jsou parametrické rovnice následující:
x(t) = (1 – t)³x₀ + 3t(1 – t)²x₁ + 3t²(1 – t)x³x₃
y(t) = (1 – t)³y₀ + 3t(1 – t)²y₁ + 3t²(1 – t)y³y + t³y₃
Nejvyšší exponent čísla 3 potvrzuje, že se jedná o krychlové polynomy. Je snadné ověřit, že když t se rovná 0, bod je (x₀, y₀), což je počáteční bod a když t se rovná 1, bod je (x₃, y₃), což je koncový bod. U počátečního tbodu (pro nízké hodnoty ), první řídicí bod (x₁, y₁) má silný účinek a u koncového bodu (vysoké hodnoty t) má druhý řídicí bod (x₁, y₁) silný účinek.
Bezierova křivka aproximace kruhových oblouků
Někdy je vhodné použít bézierovou křivku k vykreslení kruhového oblouku. Krychlový Bézierova křivka může velmi dobře odhadnout kruhový oblouk až do čtvrtinového kruhu, takže čtyři propojené Bézierovy křivky mohou definovat celý kruh. Tato aproximace je popsána ve dvou článcích publikovaných před více než 25 lety:
Tor Dokken, et al, "Good Aproximace kruhů pomocí zakřivení-Spojité Bézierovy křivky," Computer Aided Geometr Design 7 (1990), 33-41.
Michael Goldapp, "Aproximace kruhových oblouků pomocí krychlových polynomů", počítačová pomocná geometrická konstrukce 8 (1991), 227-238.
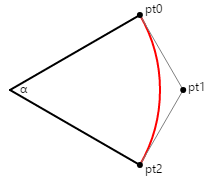
Následující diagram znázorňuje čtyři body označené , ptopt1, pt2a pt3 definování Bézierovy křivky (znázorněné červeně), která se blíží kruhové oblouku:
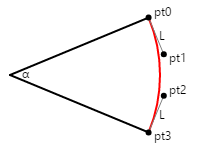
Čáry od počátečního a koncového bodu k řídicím bodům jsou tangens na kruh a bézierovou křivku a mají délku L. První článek uvedený výše označuje, že křivka Bézier nejlépe přibližuje kruhový oblouk při výpočtu této délky L takto:
L = 4 × tan(α / 4) / 3
Obrázek znázorňuje úhel 45 stupňů, takže L se rovná 0,265. V kódu by se tato hodnota vynásobila požadovaným poloměrem kruhu.
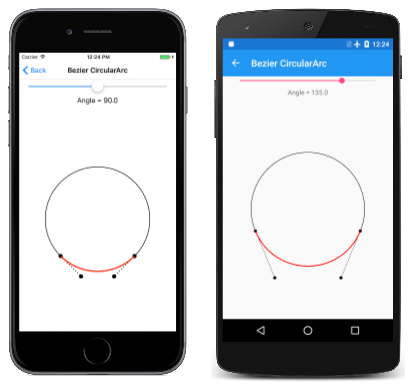
Stránka Bezier Kruhový oblouk umožňuje experimentovat s definováním křivky Bézier pro přibližný kruhový oblouk pro úhly v rozsahu až 180 stupňů. Soubor BezierCircularArcPage.xaml vytvoří SKCanvasView instanci a pro Slider výběr úhlu. Obslužná rutina PaintSurface události v souboru BezierCircularArgPage.xaml.cs kódu používá transformaci k nastavení bodu (0, 0) na střed plátna. Nakreslí kruh uprostřed tohoto bodu pro porovnání a pak vypočítá dva kontrolní body pro Bézierův křivku:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 3;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate length of control point line
float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the end points
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point3 = new SKPoint(radius * sin, radius * cos);
// Find the control points
SKPoint point0Normalized = Normalize(point0);
SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
-length * point0Normalized.X);
SKPoint point3Normalized = Normalize(point3);
SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
length * point3Normalized.X);
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);
// Draw the Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.CubicTo(point1, point2, point3);
canvas.DrawPath(path, redStroke);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
Počáteční a koncové body (point0 a point3) se počítají na základě normálních parametrických rovnic kruhu. Vzhledem k tomu, že kruh je zarovnaný na střed (0, 0), mohou být tyto body také považovány za paprskové vektory ze středu kruhu na obvod. Kontrolní body jsou na řádcích, které jsou tangens kruhu, takže jsou v pravých úhlech těchto paprskových vektorů. Vektor v pravém úhlu k jinému je jednoduše původní vektor se souřadnicemi X a Y prohozenými a jedním z nich byl negativní.
Tady je program spuštěný s různými úhly:
Podívejte se pozorně na třetí snímek obrazovky a uvidíte, že křivka Bézier se výrazně odchyluje od půlkruhu, když úhel je 180 stupňů, ale obrazovka iOS ukazuje, že se zdá, že se vejde čtvrtinový kruh přesně v pořádku, když úhel je 90 stupňů.
Výpočet souřadnic dvou kontrolních bodů je poměrně snadný, když je kruh čtvrtletí orientovaný takto:
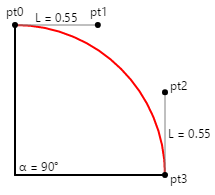
Pokud je poloměr kruhu 100, pak L je 55, a to je snadné číslo zapamatovat.
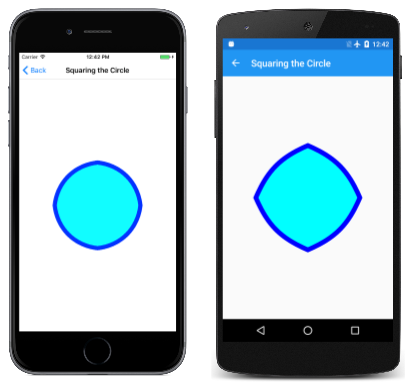
Stránka Squaring the Circle animuje obrázek mezi kruhem a čtvercem. Kruh je přibližný čtyřmi křivkami Bézier, jejichž souřadnice jsou zobrazeny v prvním sloupci této definice pole ve SquaringTheCirclePage třídě:
public class SquaringTheCirclePage : ContentPage
{
SKPoint[,] points =
{
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() },
{ new SKPoint( 55, 100), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 55), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 0), new SKPoint( 125, 0), new SKPoint() },
{ new SKPoint( 100, -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 0, -100), new SKPoint( 0, -125), new SKPoint() },
{ new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, 0), new SKPoint( -125, 0), new SKPoint() },
{ new SKPoint(-100, 55), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( -55, 100), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() }
};
...
}
Druhý sloupec obsahuje souřadnice čtyř Bézierových křivek, které definují čtverec, jehož oblast je přibližně stejná jako oblast kruhu. (Nakreslení čtvereku s přesnou oblastí jako daného kruhu je klasický nesolvitelný geometrický problém se squaringem kruhu.) Pro vykreslení čtverce s Bézierovými křivkami jsou dva řídicí body pro každou křivku stejné a jsou kolineární se počátečními a koncovými body, takže křivka Bézier je vykreslena jako přímka.
Třetí sloupec pole je určen pro interpolované hodnoty animace. Stránka nastaví časovač pro 16 milisekund a obslužná rutina PaintSurface se volá podle této rychlosti:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));
// Interpolate
TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
float t = (float)(timeSpan.TotalSeconds % 3 / 3); // 0 to 1 every 3 seconds
t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2; // 0 to 1 to 0 sinusoidally
for (int i = 0; i < 13; i++)
{
points[i, 2] = new SKPoint(
(1 - t) * points[i, 0].X + t * points[i, 1].X,
(1 - t) * points[i, 0].Y + t * points[i, 1].Y);
}
// Create the path and draw it
using (SKPath path = new SKPath())
{
path.MoveTo(points[0, 2]);
for (int i = 1; i < 13; i += 3)
{
path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
}
path.Close();
canvas.DrawPath(path, cyanFill);
canvas.DrawPath(path, blueStroke);
}
}
Body jsou interpolovány na základě sinusově oscilující hodnoty t. Interpolované body se pak používají k vytvoření řady čtyř propojených Bézierových křivek. Tady je spuštěná animace:
Taková animace by byla nemožné bez křivek, které jsou algoritmicky dostatečně flexibilní, aby se vykreslovaly jako kruhové oblouky i rovné čáry.
Stránka Bezier Infinity také využívá schopnost Bézierovy křivky k přibližné kruhové oblouku. Tady je obslužná rutina PaintSurface z BezierInfinityPage třídy:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.MoveTo(0, 0); // Center
path.CubicTo( 50, -50, 95, -100, 150, -100); // To top of right loop
path.CubicTo( 205, -100, 250, -55, 250, 0); // To far right of right loop
path.CubicTo( 250, 55, 205, 100, 150, 100); // To bottom of right loop
path.CubicTo( 95, 100, 50, 50, 0, 0); // Back to center
path.CubicTo( -50, -50, -95, -100, -150, -100); // To top of left loop
path.CubicTo(-205, -100, -250, -55, -250, 0); // To far left of left loop
path.CubicTo(-250, 55, -205, 100, -150, 100); // To bottom of left loop
path.CubicTo( -95, 100, -50, 50, 0, 0); // Back to center
path.Close();
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
Může být vhodné vykreslit tyto souřadnice na grafovém papíru, abyste zjistili, jak souvisí. Nekonečné znaménko je uprostřed kolem bodu (0, 0) a dvě smyčky mají středy (–150, 0) a (150, 0) a radii 100. V řadě příkazů můžete vidět souřadnice X kontrolních CubicTo bodů, které přebírají hodnoty –95 a –205 (tyto hodnoty jsou –150 plus a minus 55), 205 a 95 (150 plus a minus 55), stejně jako 250 a –250 pro pravé a levé strany. Jedinou výjimkou je, když se nekonečné znaménko kříží ve středu. V takovém případě mají kontrolní body souřadnice s kombinací 50 a –50, aby se křivka v blízkosti středu vyrovnala.
Tady je znaménko nekonečna:
Je poněkud plynulejší směrem ke středu než znaménko nekonečna vykreslené stránkou Arc Infinity ze tří způsobů kreslení článku Oblouk .
Kvadratická Bézierova křivka
Kvadratická křivka Bézier má pouze jeden řídicí bod a křivka je definována pouze třemi body: počátečním bodem, kontrolním bodem a koncovým bodem. Parametrické rovnice jsou velmi podobné krychlové Bézierové křivkě s tím rozdílem, že nejvyšší exponent je 2, takže křivka je kvadratický polynom:
x(t) = (1 – t)²x₀ + 2t(1 – t)x₁ + t²x entity
y(t) = (1 – t)²y₀ + 2t(1 – t)y₁ + t²y účely
Chcete-li přidat kvadratickou Bézierovou křivku do cesty, použijte QuadTo metodu QuadTo nebo přetížení s samostatnými x a y souřadnicemi:
public void QuadTo (SKPoint point1, SKPoint point2)
public void QuadTo (Single x1, Single y1, Single x2, Single y2)
Metody přidají křivku z aktuální pozice na point2point1 řídicí bod.
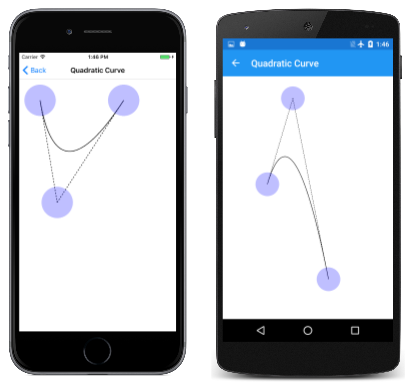
Můžete experimentovat s kvadratické Bézierovy křivky se stránkou Kvadratické křivky, která je velmi podobná stránce BezierOvy křivky s výjimkou, že má pouze tři dotykové body. Tady je PaintSurface obslužná rutina v souboru QuadraticCurve.xaml.cs kódu:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with quadratic Bezier
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.QuadTo(touchPoints[1].Center,
touchPoints[2].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
A tady běží:
Tečkované čáry jsou tangens k křivkě na začátku a koncovém bodu a splňují se v řídicím bodě.
Kvadratický Bézier je dobrý, pokud potřebujete křivku obecného tvaru, ale dáváte přednost pohodlí pouze jednoho kontrolního bodu, nikoli dvou. Kvadratický Bézier se vykreslí efektivněji než jakákoli jiná křivka, což je důvod, proč se používá interně v Skia k vykreslení eliptických oblouků.
Tvar kvadratické křivky Bézier však není eliptický, což je důvod, proč jsou k přibližné eliptickému oblouku vyžadovány kvadratické Béziers. Kvadratický Bézier je místo segmentu paraboly.
Kuželová Bézierova křivka
Kosnicová Bézierova křivka, označovaná také jako kvadratická křivka Bézier, je relativně nedávným doplňkem k rodině Bézierových křivek. Podobně jako kvadratická křivka Bézier zahrnuje kvadratickou bézierovou křivku počáteční bod, koncový bod a jeden kontrolní bod. Ale kvadratická křivka Bézier také vyžaduje hodnotu hmotnosti . Říká se tomu logické kvadratické, protože parametrické vzorce zahrnují poměry.
Parametrické rovnice pro X a Y jsou poměry, které sdílejí stejný jmenovatel. Tady je rovnice jmenovatele pro t od 0 do 1 a hodnotu váhy w:
d(t) = (1 – t)² + 2wt(1 – t) + t²
Teorii, racionalizace kvadratika může zahrnovat tři samostatné hodnoty hmotnosti, jednu pro každý ze tří termínů, ale lze je zjednodušit pouze na jednu hodnotu váhy v prostředním termínu.
Parametrické rovnice souřadnic X a Y jsou podobné parametrickým rovnicím pro kvadratický Bézier s tím rozdílem, že střední termín obsahuje také hodnotu váhy a výraz je rozdělen jmenovatelem:
x(t) = ((1 – t)²x₀ + 2wt(1 – t)x₁ + t²x²)) ÷ d(t)
y(t) = ((1 – t)²y₀ + 2wt(1 – t)y₁ + t²y²)) ÷ d(t)
Logické kvadratické Bézierovy křivky se také označují jako kuželové křivky , protože mohou přesně představovat segmenty libovolné kuželové části – hyperbolas, parabolas, tři tečky a kruhy.
Chcete-li přidat racionalizální kvadratickou Bézierovou křivku do cesty, použijte ConicTo metodu ConicTo nebo přetížení s samostatnými x a y souřadnicemi:
public void ConicTo (SKPoint point1, SKPoint point2, Single weight)
public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)
Všimněte si posledního weight parametru.
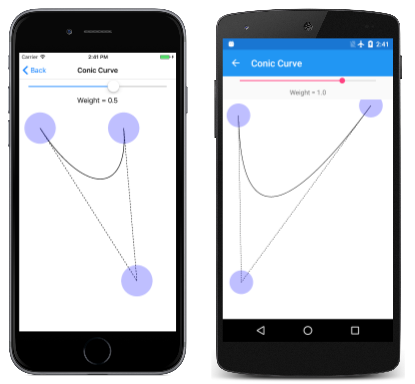
Stránka Kuželová křivka umožňuje experimentovat s těmito křivkami. Třída ConicCurvePage je odvozena z InteractivePage. Soubor ConicCurvePage.xaml vytvoří instanci pro Slider výběr hodnoty váhy mezi -2 a 2. Soubor ConicCurvePage.xaml.cs kódem vytvoří tři TouchPoint objekty a PaintSurface obslužná rutina jednoduše vykresluje výslednou křivku s tangensovými čárami do kontrolních bodů:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with conic curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ConicTo(touchPoints[1].Center,
touchPoints[2].Center,
(float)weightSlider.Value);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Tady je spuštěný:
Jak vidíte, zdá se, že řídicí bod vytáhne křivku směrem k ní více, když je váha vyšší. Když je váha nula, křivka se změní na přímku od počátečního bodu do koncového bodu.
Teoreticky jsou povoleny záporné váhy a způsobují, že křivka se ohýbá od kontrolního bodu. Váhy –1 nebo nižší však způsobují, že jmenovatel v parametrických rovnicích se záporně stane pro konkrétní hodnoty t. Z tohoto důvodu jsou záporná váhy ignorovány v ConicTo metodách. Program Conic Curve umožňuje nastavit záporné váhy, ale jak můžete vidět experimentováním, záporné váhy mají stejný účinek jako váha nuly a způsobit vykreslení rovné čáry.
Je velmi snadné odvodit kontrolní bod a váhu použít metodu ConicTo kreslení kruhového oblouku nahoru (ale ne včetně) sémikulárního kruhu. V následujícím diagramu se tečné čáry od počátečního a koncového bodu scházejí v řídicím bodě.
Trigonometrii můžete použít k určení vzdálenosti kontrolního bodu od středu kruhu: Jedná se o poloměr kruhu dělený kosinusem poloviny úhlu α. Pokud chcete nakreslit kruhový oblouk mezi počátečním a koncovými body, nastavte váhu na stejný kosinus poloviny úhlu. Všimněte si, že pokud je úhel 180 stupňů, tečny se nikdy nesplní a váha je nula. Ale pro úhly menší než 180 stupňů funguje matematika dobře.
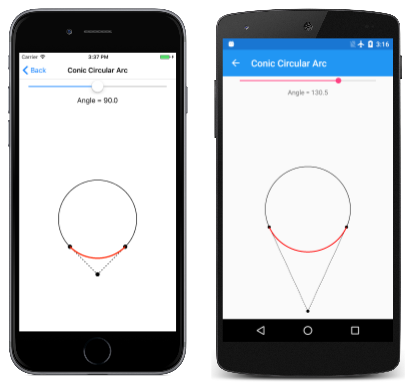
To ukazuje stránka Kuželový kruhový oblouk. Soubor ConicCircularArc.xaml vytvoří Slider instanci pro výběr úhlu. Obslužná rutina PaintSurface v souboru ConicCircularArc.xaml.cs kódem vypočítá řídicí bod a váhu:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 4;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the points and weight
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point1 = new SKPoint(0, radius / cos);
SKPoint point2 = new SKPoint(radius * sin, radius * cos);
float weight = cos;
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);
// Draw the conic
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.ConicTo(point1, point2, weight);
canvas.DrawPath(path, redStroke);
}
}
Jak vidíte, neexistuje žádný vizuální rozdíl mezi ConicTo cestou zobrazenou červenou a podkladovým kruhem zobrazeným pro referenci:
Ale nastavte úhel na 180 stupňů a matematika selže.
V tomto případě je nešťastné, že ConicTo nepodporuje záporné váhy, protože teoreticky (na základě parametrických rovnic) lze kruh dokončit dalším voláním se ConicTo stejnými body, ale zápornou hodnotou váhy. To by umožnilo vytvořit celý kruh s pouhými dvěma ConicTo křivkami na základě libovolného úhlu mezi (ale ne zahrnutím) nula stupňů a 180 stupňů.