Tři způsoby, jak nakreslit oblouk

Naučte se používat SkiaSharp k definování oblouků třemi různými způsoby.

Oblouk je křivka na obvodu elipsy, jako jsou zaoblené části tohoto nekonečna:

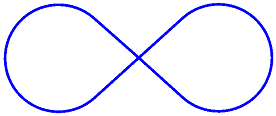
Navzdory jednoduchosti této definice neexistuje způsob, jak definovat funkci kreslení oblouku, která splňuje každou potřebu, a proto žádný konsensus mezi grafickými systémy nejlepšího způsobu kreslení oblouku. Z tohoto důvodu SKPath se třída neomezuje pouze na jeden přístup.

SKPath definuje metodu AddArc , pět různých ArcTo metod a dvě relativní RArcTo metody. Tyto metody spadají do tří kategorií, které představují tři velmi odlišné přístupy k určení oblouku. Který z nich použijete, závisí na informacích dostupných k definování oblouku a na tom, jak tento oblouk zapadá do jiné grafiky, kterou kreslíte.

Úhel oblouku

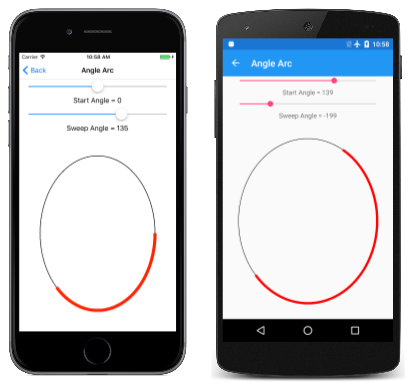
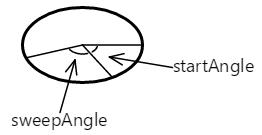
Úhel oblouku při kreslení oblouků vyžaduje, abyste zadali obdélník, který ohraničuje tři tečky. Oblouk na obvodu tohoto elipsy je označen úhly ze středu elipsy, které označují začátek oblouku a jeho délku. Dvě různé metody vykreslují úhlové oblouky. Jedná se o metodu AddArc a metodu ArcTo :

public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)

public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)

Tyto metody jsou identické s metodami Android AddArc a [ArcTo]xref:Android.Graphics.Path.ArcTo*). Metoda iOS AddArc je podobná, ale je omezena na oblouky na obvodu kruhu, nikoli na zobecněné na tři tečky.

Obě metody začínají SKRect hodnotou, která definuje umístění i velikost tří teček:

Oblouk je součástí obvodu tohoto elipsy.

Argument startAngle je úhel ve stupních ve směru hodinových ručiček vzhledem k vodorovné čáře nakreslené ze středu elipsy vpravo. Argument sweepAngle je relativní vzhledem k argumentu startAngle. Tady jsou startAngle sweepAngle hodnoty 60 stupňů a 100 stupňů, v uvedeném pořadí:

Oblouk začíná počátečním úhlem. Jeho délka se řídí úhlem úklidu. Oblouk je zde zobrazen červeně:

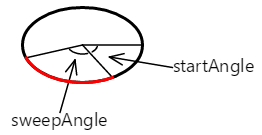
Křivka přidaná k cestě pomocí AddArc nebo ArcTo metody je jednoduše ta část obvodu tří teček:

sweepAngle Argumenty startAngle můžou být záporné: Oblouk je ve směru hodinových ručiček pro kladné hodnoty sweepAngle a proti směru hodinových ručiček pro záporné hodnoty.

AddArc Nedefinuje však uzavřený obrys. Pokud zavoláte LineTo za AddArc, přímka je nakreslena z konce oblouku k bodu v LineTo metodě, a totéž platí pro ArcTo.

AddArc automaticky spustí nový obrys a je funkčně ekvivalentní volání ArcTo s konečným argumentem true:

path.ArcTo (oval, startAngle, sweepAngle, true);

Tento poslední argument je volána forceMoveToa účinně způsobuje MoveTo volání na začátku oblouku. To začíná novou obrysovou křivkou. To není případ posledního argumentu false:

path.ArcTo (oval, startAngle, sweepAngle, false);

Tato verze ArcTo nakreslí čáru z aktuální pozice na začátek oblouku. To znamená, že oblouk může být někde uprostřed většího obrysu.

Stránka Úhel oblouku umožňuje pomocí dvou posuvníků určit počáteční a uklidit úhly. Soubor XAML vytvoří instanci dvou Slider prvků a objektu SKCanvasView. Obslužná rutina PaintCanvas v souboru AngleArcPage.xaml.cs nakreslí ovál i oblouk pomocí dvou SKPaint objektů definovaných jako pole:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
    float startAngle = (float)startAngleSlider.Value;
    float sweepAngle = (float)sweepAngleSlider.Value;

    canvas.DrawOval(rect, outlinePaint);

    using (SKPath path = new SKPath())
    {
        path.AddArc(rect, startAngle, sweepAngle);
        canvas.DrawPath(path, arcPaint);
    }
}

Jak vidíte, počáteční úhel i úhel úklidu můžou mít záporné hodnoty:

Tento přístup k generování oblouku je algoritmicky nejjednodušší a je snadné odvodit parametrické rovnice popisující oblouk. Znalost velikosti a umístění tří teček a úhlů startu a úklidu lze počáteční a koncové body oblouku vypočítat pomocí jednoduché trigonometrické funkce:

x = oval.MidX + (oval.Width / 2) * cos(angle)

y = oval.MidY + (oval.Height / 2) * sin(angle)

Hodnota angle je buď startAngle nebo startAngle + sweepAngle.

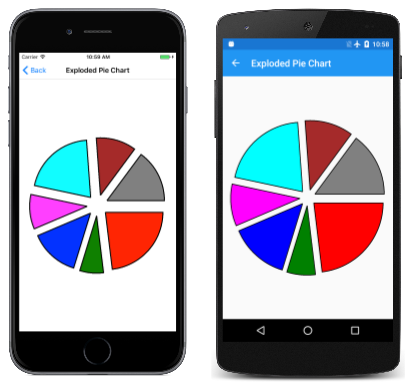
Použití dvou úhlů k definování oblouku je nejvhodnější pro případy, kdy znáte úhlovou délku oblouku, který chcete nakreslit, například k vytvoření výsečového grafu. To ukazuje stránka Rozložený výsečový graf . Třída ExplodedPieChartPage používá interní třídu k definování některých fabricated dat a barev:

class ChartData
{
    public ChartData(int value, SKColor color)
    {
        Value = value;
        Color = color;
    }

    public int Value { private set; get; }

    public SKColor Color { private set; get; }
}

ChartData[] chartData =
{
    new ChartData(45, SKColors.Red),
    new ChartData(13, SKColors.Green),
    new ChartData(27, SKColors.Blue),
    new ChartData(19, SKColors.Magenta),
    new ChartData(40, SKColors.Cyan),
    new ChartData(22, SKColors.Brown),
    new ChartData(29, SKColors.Gray)
};

Obslužná rutina PaintSurface nejprve prochází položky k výpočtu totalValues čísla. Z toho může určit velikost každé položky jako zlomek součtu a převést ji na úhel:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    int totalValues = 0;

    foreach (ChartData item in chartData)
    {
        totalValues += item.Value;
    }

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float explodeOffset = 50;
    float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
    SKRect rect = new SKRect(center.X - radius, center.Y - radius,
                             center.X + radius, center.Y + radius);

    float startAngle = 0;

    foreach (ChartData item in chartData)
    {
        float sweepAngle = 360f * item.Value / totalValues;

        using (SKPath path = new SKPath())
        using (SKPaint fillPaint = new SKPaint())
        using (SKPaint outlinePaint = new SKPaint())
        {
            path.MoveTo(center);
            path.ArcTo(rect, startAngle, sweepAngle, false);
            path.Close();

            fillPaint.Style = SKPaintStyle.Fill;
            fillPaint.Color = item.Color;

            outlinePaint.Style = SKPaintStyle.Stroke;
            outlinePaint.StrokeWidth = 5;
            outlinePaint.Color = SKColors.Black;

            // Calculate "explode" transform
            float angle = startAngle + 0.5f * sweepAngle;
            float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
            float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);

            canvas.Save();
            canvas.Translate(x, y);

            // Fill and stroke the path
            canvas.DrawPath(path, fillPaint);
            canvas.DrawPath(path, outlinePaint);
            canvas.Restore();
        }

        startAngle += sweepAngle;
    }
}

Pro každý výseč se vytvoří nový SKPath objekt. Cesta se skládá z čáry ze středu, potom ArcTo k nakreslení oblouku a další čáry zpět do středu výsledků Close volání. Tento program zobrazí rozložené výsečové výseče tak, že je přesunete ze středu o 50 pixelů. Tento úkol vyžaduje vektor ve směru středu úhlu úklidu pro každý řez:

Pokud chcete zjistit, jak to vypadá bez výbuchu, jednoduše okomentujte Translate volání:

Tečná oblouk

Druhým typem oblouku, který SKPath podporuje, je tangens oblouk, který se nazývá, protože oblouk je obvod kruhu, který je tangens na dvě propojené čáry.

K cestě se přidá tangentní oblouk s voláním ArcTo metody se dvěma SKPoint parametry nebo ArcTo přetížení s samostatnými Single parametry pro body:

public void ArcTo (SKPoint point1, SKPoint point2, Single radius)

public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)

Tato ArcTo metoda je podobná funkci jazyk PostScript arct (strana 532) a metodu iOSAddArcToPoint.

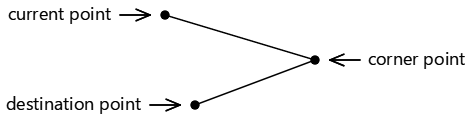
Metoda ArcTo zahrnuje tři body:

• Aktuální bod obrysu nebo bod (0, 0), pokud MoveTo nebyl volána
• První argument bodu metody ArcTo , který se nazývá rohový bod
• Druhý argument ArcTobodu , který se nazývá cílový bod:

Tyto tři body definují dvě propojené čáry:

Pokud jsou tři body kolineární – to znamená, že pokud leží na stejné přímce – nebude nakreslen žádný oblouk.

Metoda ArcTo obsahuje radius také parametr. Tím se definuje poloměr kruhu:

Tangens oblouk není zobecněn pro tři tečky.

Pokud se tyto dvě čáry shodují v libovolném úhlu, lze tento kruh vložit mezi tyto čáry, aby byl tangens na obě čáry:

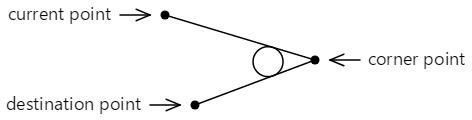
Křivka přidaná do obrysu se nedotkne žádného z bodů zadaných ArcTo v metodě. Skládá se z přímky od aktuálního bodu k prvnímu tangensovému bodu a oblouku, který končí na druhém tangensovém bodu, který je znázorněn červeně:

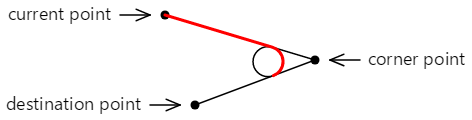
Tady je poslední přímka a oblouk, který se přidá do obrysu:

Obrys lze pokračovat od druhého tangens bodu.

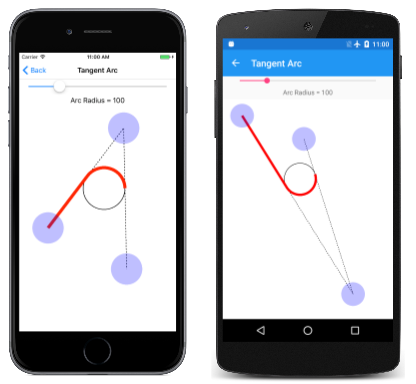
Stránka Tangent Arc umožňuje experimentovat s tangensovým obloukem. Toto je první z několika stránek, které jsou odvozeny od InteractivePage, který definuje několik užitečných SKPaint objektů a provádí TouchPoint zpracování:

public class InteractivePage : ContentPage
{
    protected SKCanvasView baseCanvasView;
    protected TouchPoint[] touchPoints;

    protected SKPaint strokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3
    };

    protected SKPaint redStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Red,
        StrokeWidth = 15
    };

    protected SKPaint dottedStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3,
        PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
    };

    protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
    {
        bool touchPointMoved = false;

        foreach (TouchPoint touchPoint in touchPoints)
        {
            float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
            SKPoint point = new SKPoint(scale * (float)args.Location.X,
                                        scale * (float)args.Location.Y);
            touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
        }

        if (touchPointMoved)
        {
            baseCanvasView.InvalidateSurface();
        }
    }
}

Třída TangentArcPage je odvozena z InteractivePage. Konstruktor v souboru TangentArcPage.xaml.cs je zodpovědný za vytvoření instance a inicializaci touchPoints pole a nastavení baseCanvasView (inInteractivePage) na SKCanvasView objekt instance v souboru TangentArcPage.xaml:

public partial class TangentArcPage : InteractivePage
{
    public TangentArcPage()
    {
        touchPoints = new TouchPoint[3];

        for (int i = 0; i < 3; i++)
        {
            TouchPoint touchPoint = new TouchPoint
            {
                Center = new SKPoint(i == 0 ? 100 : 500,
                                     i != 2 ? 100 : 500)
            };
            touchPoints[i] = touchPoint;
        }

        InitializeComponent();

        baseCanvasView = canvasView;
        radiusSlider.Value = 100;
    }

    void sliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        if (canvasView != null)
        {
            canvasView.InvalidateSurface();
        }
    }
    ...
}

Obslužná PaintSurface rutina používá metodu ArcTo k vykreslení oblouku na základě dotykových bodů a a Slider, ale také algoritmicky vypočítá kruh, na který je úhel založen:

public partial class TangentArcPage : InteractivePage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Draw the two lines that meet at an angle
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.LineTo(touchPoints[1].Center);
            path.LineTo(touchPoints[2].Center);
            canvas.DrawPath(path, dottedStrokePaint);
        }

        // Draw the circle that the arc wraps around
        float radius = (float)radiusSlider.Value;

        SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
        SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);

        double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
        double angleBetween = Math.Acos(dotProduct);
        float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
        SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
        SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
                                     touchPoints[1].Center.Y + vMid.Y * hypotenuse);

        canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);

        // Draw the tangent arc
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
            canvas.DrawPath(path, redStrokePaint);
        }

        foreach (TouchPoint touchPoint in touchPoints)
        {
            touchPoint.Paint(canvas);
        }
    }

    // Vector methods
    SKPoint Normalize(SKPoint v)
    {
        float magnitude = Magnitude(v);
        return new SKPoint(v.X / magnitude, v.Y / magnitude);
    }

    float Magnitude(SKPoint v)
    {
        return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
    }
}

Tady je stránka Tangent Arc spuštěná:

Tangens oblouk je ideální pro vytváření zaoblených rohů, jako je zaoblený obdélník. Vzhledem k tomu SKPath , že již obsahuje metodu AddRoundedRect , stránka Round Heptagon ukazuje, jak použít ArcTo k zaoblení rohů sedmistranného mnohoúhelníku. (Kód je zobecněn pro všechny běžné mnohoúhelníky.)

Obslužná PaintSurface rutina RoundedHeptagonPage třídy obsahuje jednu for smyčku pro výpočet souřadnic sedmi vrcholů heptagonu a sekundu pro výpočet středních bodů sedmi stran z těchto vrcholů. Tyto střední body se pak použijí k vytvoření cesty:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    float cornerRadius = 100;
    int numVertices = 7;
    float radius = 0.45f * Math.Min(info.Width, info.Height);

    SKPoint[] vertices = new SKPoint[numVertices];
    SKPoint[] midPoints = new SKPoint[numVertices];

    double vertexAngle = -0.5f * Math.PI;       // straight up

    // Coordinates of the vertices of the polygon
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
                                       radius * (float)Math.Sin(vertexAngle));
        vertexAngle += 2 * Math.PI / numVertices;
    }

    // Coordinates of the midpoints of the sides connecting the vertices
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        int prevVertex = (vertex + numVertices - 1) % numVertices;
        midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
                                        (vertices[prevVertex].Y + vertices[vertex].Y) / 2);
    }

    // Create the path
    using (SKPath path = new SKPath())
    {
        // Begin at the first midpoint
        path.MoveTo(midPoints[0]);

        for (int vertex = 0; vertex < numVertices; vertex++)
        {
            SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];

            // Draws a line from the current point, and then the arc
            path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);

            // Connect the arc with the next midpoint
            path.LineTo(nextMidPoint);
        }
        path.Close();

        // Render the path in the center of the screen
        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 10;

            canvas.Translate(info.Width / 2, info.Height / 2);
            canvas.DrawPath(path, paint);
        }
    }
}

Tady je spuštěný program:

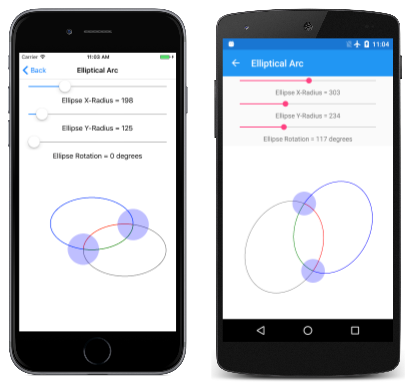
Eliptický oblouk

Eliptický oblouk se přidá do cesty s voláním ArcTo metody, která má dva SKPoint parametry, nebo ArcTo přetížení s samostatnými souřadnicemi X a Y:

public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)

public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)

Eliptický oblouk je konzistentní s eliptickým obloukem, který je součástí SVG (Scalable Vector Graphics) a třídy Univerzální platforma WindowsArcSegment.

Tyto ArcTo metody nakreslí oblouk mezi dvěma body, což jsou aktuální bod obrysu, a poslední parametr metody ArcTo ( xy parametr nebo samostatný x a y parametry):

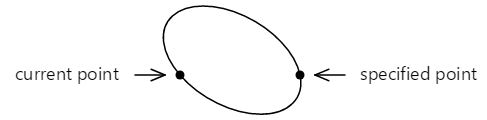
Parametr prvního bodu metody ArcTo (rnebo rx a ry) není vůbec bod, ale místo toho určuje vodorovnou a svislou radii tří teček;

Parametr xAxisRotate je počet stupňů ve směru hodinových ručiček pro otočení tohoto elipsy:

Pokud je tato nakloněná elipsa pak umístěna tak, aby se dotýkala dvou bodů, body jsou spojené dvěma různými oblouky:

Tyto dva oblouky lze rozlišit dvěma způsoby: Horní oblouk je větší než dolní oblouk a jak je oblouk kreslen zleva doprava, horní oblouk je vykreslen ve směru hodinových ručiček, zatímco dolní oblouk je nakreslený proti směru hodinových ručiček.

Je také možné přizpůsobit tři tečky mezi těmito dvěma body jiným způsobem:

Teď je nakreslený menší oblouk, který je nakreslený po směru hodinových ručiček, a větší oblouk v dolní části, který je nakreslený proti směru hodinových ručiček.

Tyto dva body lze proto spojit obloukem definovaným nakloněným třemi tečkou celkem čtyřmi způsoby:

Tyto čtyři oblouky jsou odlišeny čtyřmi kombinacemi SKPathArcSize argumentů typu výčtu SKPathDirection metody ArcTo :

• červená: SKPathArcSize.Large a SKPathDirection.Clockwise
• zelená: SKPathArcSize.Small a SKPathDirection.Clockwise
• modrá: SKPathArcSize.Small a SKPathDirection.CounterClockwise
• magenta: SKPathArcSize.Large a SKPathDirection.CounterClockwise

Pokud nakloněná elipsa není dostatečně velká, aby se vešla mezi dva body, je rovnoměrně škálovaná, dokud nebude dostatečně velká. V takovém případě tyto dva body spojují pouze dva jedinečné oblouky. Tyto hodnoty lze rozlišit pomocí parametru SKPathDirection .

I když tento přístup k definování oblouku při prvním setkání zní komplexně, je to jediný přístup, který umožňuje definovat oblouk s otočenou elipsou, a to je často nejjednodušší přístup, když potřebujete integrovat oblouky s jinými částmi obrysu.

Stránka Elliptical Arc umožňuje interaktivně nastavit dva body a velikost a otočení tří teček. Třída EllipticalArcPage je odvozena od InteractivePagea PaintSurface obslužná rutina v souboru EllipticalArcPage.xaml.cs kód-behind nakreslí čtyři oblouky:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        int colorIndex = 0;
        SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
                                          (float)yRadiusSlider.Value);
        float rotation = (float)rotationSlider.Value;

        foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
            foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
            {
                path.MoveTo(touchPoints[0].Center);
                path.ArcTo(ellipseSize, rotation,
                           arcSize, direction,
                           touchPoints[1].Center);

                strokePaint.Color = colors[colorIndex++];
                canvas.DrawPath(path, strokePaint);
                path.Reset();
            }
    }

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

Tady je spuštěný:

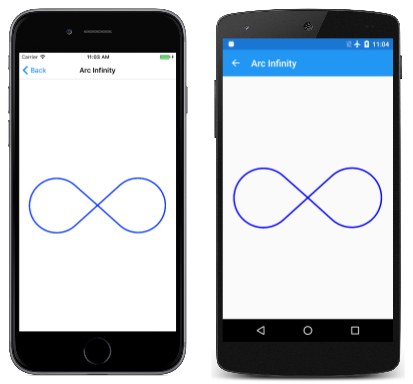
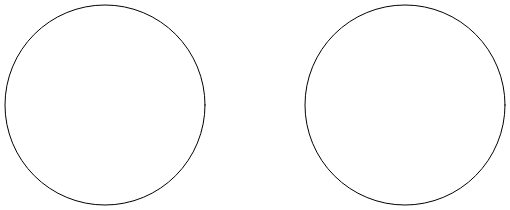
Stránka Arc Infinity používá eliptický oblouk k vykreslení nekonečna znaménka. Znaménko nekonečna je založeno na dvou kruhech s paprsky 100 jednotek oddělených 100 jednotkami:

Dvě čáry, které se vzájemně protínají, jsou tangens pro oba kruhy:

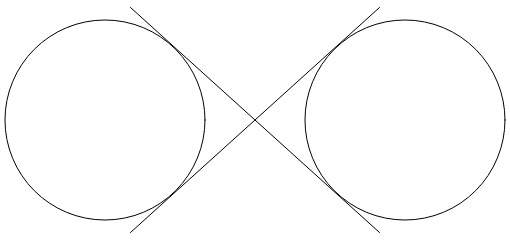
Nekonečné znaménko je kombinací částí těchto kruhů a dvou čar. Chcete-li použít eliptický oblouk k vykreslení nekonečna znaménka, musí být určeny souřadnice, kde jsou dvě čáry tangens k kruhům.

Vytvořte pravý obdélník v jednom z kruhů:

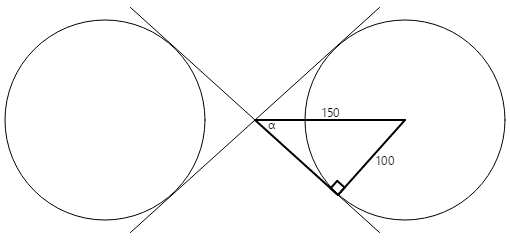
Poloměr kruhu je 100 jednotek a hypotenuse trojúhelníku je 150 jednotek, takže úhel α je arkusine (inverzní sinus) 100 dělený 150 nebo 41,8 stupňů. Délka druhé strany trojúhelníku je 150krát kosinus 41,8 stupňů, nebo 112, které lze vypočítat také Pythagorským teorémem.

Souřadnice tangensového bodu je pak možné vypočítat pomocí těchto informací:

x = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

Čtyři tangensové body jsou vše, co je nutné k vykreslení nekonečna znaménka uprostřed bodu (0, 0) s kruhem radii 100:

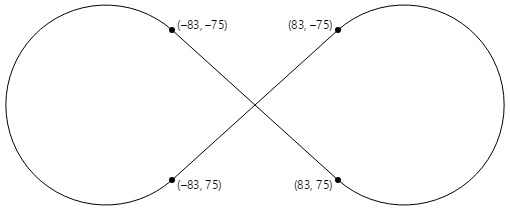
Obslužná rutina PaintSurface ve ArcInfinityPage třídě umístí znaménko nekonečna tak, aby bod (0, 0) byl umístěn uprostřed stránky a škáluje cestu na velikost obrazovky:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.LineTo(83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
        path.LineTo(-83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
        path.Close();

        // Use path.TightBounds for coordinates without control points
        SKRect pathBounds = path.Bounds;

        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(Math.Min(info.Width / pathBounds.Width,
                              info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

Kód pomocí Bounds vlastnosti SKPath určuje rozměry nekonečna sinus k jeho škálování na velikost plátna:

Výsledek vypadá trochu málo, což naznačuje, že Bounds vlastnost SKPath hlásí větší velikost než cesta.

Skia interně přibližuje oblouk pomocí více kvadratických Bézierových křivek. Tyto křivky (jak uvidíte v další části) obsahují kontrolní body, které určují, jak se křivka vykresluje, ale nejsou součástí vykreslené křivky. Tato Bounds vlastnost zahrnuje tyto řídicí body.

Pokud chcete získat užší fit, použijte TightBounds vlastnost, která vylučuje kontrolní body. Tady je program spuštěný v režimu na šířku TightBounds a pomocí vlastnosti získat hranice cesty:

I když jsou spojení mezi oblouky a rovnými čárami matematicky hladké, změna z oblouku na přímku může vypadat trochu náhle. Lepší nekonečno znaménko je prezentováno v dalším článku o třech typech Bézierovy křivky.

Související odkazy

• Rozhraní API SkiaSharp