Vyhodnocení funkce pravděpodobnosti
Důležité
Podpora studia Machine Learning (Classic) skončí 31. srpna 2024. Doporučujeme do tohoto data přejít na službu Azure Machine Learning.
Od 1. prosince 2021 nebude možné vytvářet nové prostředky studia Machine Learning (Classic). Do 31. srpna 2024 můžete pokračovat v používání stávajících prostředků studia Machine Learning (Classic).
- Přečtěte si informace o přesouvání projektů strojového učení z ML Studia (classic) na Azure Machine Learning.
- Přečtěte si další informace o Azure Machine Learning.
Dokumentace ke studiu ML (Classic) se vyřazuje z provozu a v budoucnu se nemusí aktualizovat.
Odpovídá zadané distribuční funkci pravděpodobnosti do datové sady.
Kategorie: Statistické funkce
Poznámka
Platí jenom pro: Machine Learning Studio (jenom Classic)
Podobné moduly pro přetažení jsou k dispozici v návrháři Azure Machine Learning.
Přehled modulu
Tento článek popisuje, jak pomocí modulu Vyhodnotit funkci pravděpodobnosti v nástroji Machine Learning Studio (classic) vypočítat statistické míry, které popisují rozdělení sloupce, jako jsou Bernoulli, Pareto nebo Poissonova rozdělení.
Pokud chcete tento model použít, připojte datovou sadu, která obsahuje aspoň jeden sloupec číselných hodnot, a zvolte rozdělení pravděpodobnosti, které chcete otestovat. Modul vrátí tabulku dat obsahující hodnoty ze zadané funkce pravděpodobnosti.
Pro zvolené rozdělení pravděpodobnosti můžete vypočítat některou z těchto hodnot:
- kumulativní distribuční funkce (cdf)
- inverzní kumulativní distribuční funkce (InverseCdf)
- funkce hustoty pravděpodobnosti (Pdf)
Proč je rozdělení pravděpodobnosti užitečné?
Při vyhodnocování dat proti rozdělení pravděpodobnosti mapujete hodnoty sloupců na sadu hodnot se známými vlastnostmi. Když víte, jestli vaše data odpovídají jedné z těchto dobře známých distribucí, můžete být schopni odvodit další vlastnosti dat. Obecně můžete získat lepší předpovědi z modelu, když můžete identifikovat distribuci, která nejlépe vyhovuje datům.
Otázka, kterou funkci rozdělení pravděpodobnosti použít, závisí na datech a proměnných, které se měří. Například některé rozdělení jsou navrženy k popisu pravděpodobností diskrétních hodnot; jiné jsou určeny pouze pro průběžné číselné proměnné. U některých distribucí musíte také předem znát očekávaný průměr, stupně volnosti a tak dále. Podrobnosti najdete v tématu Podporované rozdělení pravděpodobnosti.
Konfigurace funkce Vyhodnocení pravděpodobnosti
Všechny možnosti se mění v závislosti na typu rozdělení pravděpodobnosti, který chcete vypočítat. Pokud změníte metodu rozdělení pravděpodobnosti, další výběry, které jste možná provedli, se resetují.
Proto nezapomeňte nejprve zvolit možnost Distribuce !
Datová sada použitá jako vstup by měla obsahovat číselná data. Ostatní typy dat se ignorují.
Pro každou analýzu můžete použít jednu metodu rozdělení pravděpodobnosti. Pokud chcete vypočítat jiné rozdělení pravděpodobnosti, přidejte samostatnou instanci modulu pro každou distribuci, kterou chcete testovat.
Přidejte do experimentu modul Funkce vyhodnocení pravděpodobnosti . Tento modul najdete v kategorii Statistické funkce v Machine Learning Studiu (classic).
Připojení datovou sadu, která obsahuje aspoň jeden sloupec čísel.
Pomocí možnosti Rozdělení vyberte typ rozdělení pravděpodobnosti, který chcete vypočítat. Seznam možností a jejich požadovaných argumentů najdete v části Podporované rozdělení pravděpodobnosti .
Nastavte všechny parametry, které distribuce vyžaduje.
Zvolte jednu ze tří statistik, která se má vytvořit: kumulativní distribuční funkce (cdf), inverzní kumulativní distribuční funkce (InverseCdf) nebo funkce hustoty pravděpodobnosti (pdf).
Definice najdete v části Technické poznámky.
Pomocí selektoru sloupců vyberte sloupce, u kterých se má vypočítat vybrané rozdělení pravděpodobnosti.
Všechny vybrané sloupce musí mít číselný datový typ.
Oblast dat ve sloupci musí být také platná vzhledem k vybrané funkci pravděpodobnosti. V opačném případě může dojít k chybě nebo výsledku naN.
U řídkých sloupců nebudou zpracovány všechny hodnoty odpovídající nule na pozadí.
Pomocí možnosti Režim výsledku určete, jak výstup výsledků provést. Hodnoty sloupců můžete nahradit hodnotami rozdělení pravděpodobnosti, připojit nové hodnoty k datové sadě nebo vrátit pouze hodnoty rozdělení pravděpodobnosti.
Spusťte experiment nebo klikněte pravým tlačítkem myši na modul Vyhodnotit funkci pravděpodobnosti a klikněte na Tlačítko Spustit.
Výsledky
Následující tabulka obsahuje příklad výsledků pomocí možnosti Připojit na jednom sloupci teploty z ukázkové datové sady Forest Fires .
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp | FFisher.cdf(temp |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11,4 | 1 | 1 | 0.993147 | 0.001502 |
Záhlaví vygenerovaných sloupců obsahují použitou rozdělení pravděpodobnosti.
Pokud si nejste jistí, která pravděpodobnost rozdělení pravděpodobnosti bude vyhovovat vašim datům, můžete vytvořit rychlý graf kumulativního rozdělení a hustoty pravděpodobnosti pro libovolný číselný sloupec.
- Klikněte pravým tlačítkem myši na výstup datové sady nebo modulu a vyberte Vizualizovat.
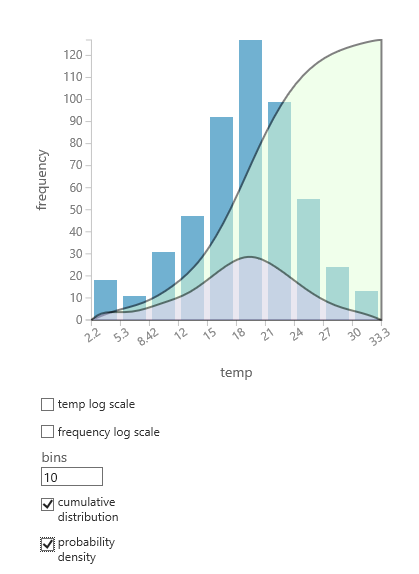
- Vyberte sloupec zájmu a v podokně Histogram vyberte kumulativní rozdělení nebo hustotu pravděpodobnosti.
- Graf rozdělení, podobně jako v následujícím příkladu, je nadsunut na histogramu představujícím data.
Podporované rozdělení pravděpodobnosti
Modul Funkce vyhodnocení pravděpodobnosti podporuje následující rozdělení:
Bernoulli
Bernoulliho rozdělení je rozdělení nad binárními hodnotami: jinými slovy, modeluje očekávané rozdělení, pokud jsou možné pouze dvě hodnoty.
Pokud chcete vypočítat, vyberte Bernoulli a nastavte následující možnosti:
- Pravděpodobnost úspěchu
Parametr p určuje pravděpodobnost, že se vygeneruje 1. Zadejte číslo (float) od 0,0 do 1,0, které určuje pravděpodobnost úspěchu. Výchozí hodnota je .5.
Beta
Beta rozdělení je souvislé jednovariátní rozdělení.
Pokud chcete vypočítat, vyberte Beta a nastavte následující možnosti:
Obrazec
Zadejte hodnotu, která změní tvar rozdělení.Parametr obrazce je libovolný parametr rozdělení pravděpodobnosti, který nedefinuje jeho umístění nebo měřítko. Proto když zadáte hodnotu obrazce, parametr změní tvar rozdělení místo přesunutí, roztažení nebo zmenšení.
Hodnota musí být číslo (
double). Výchozí hodnota je 1,0.Škálování
Zadejte číslo, které se má použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Horní mez
Zadejte číslo (double), které představuje horní mez rozdělení. Výchozí hodnota je 1,0.Dolní mez
Zadejte číslo (double), které představuje dolní mez rozdělení. Výchozí hodnota je 0,0.
Binomické
Binomické rozdělení je diskrétní jednovariátové rozdělení. Binomické rozdělení se používá k modelování počtu úspěchů ve vzorku. Nahrazení se používá při vzorkování. Pro vzorkování bez nahrazení použijte hypergeometrickou distribuci.
Pokud chcete vypočítat, vyberte Binomiál a nastavte následující možnosti:
Pravděpodobnost úspěchu
Zadejte číslo (float) mezi 0,0 a 1,0, které označuje pravděpodobnost úspěchu. Výchozí hodnota je .5.Počet pokusů
Zadejte počet pokusů.Použijte hodnotu
integers minimální hodnotou 1. Výchozí hodnota je 3.
Cauchy
Rozdělení Cauchy je symetrické průběžné rozdělení pravděpodobnosti.
Pokud chcete vypočítat, vyberte Cauchy a nastavte následující možnosti:
Umístění
Zadejte číslo (double), které představuje umístění 0. elementu.Zadáním hodnoty parametru Location můžete posunout rozdělení pravděpodobnosti nahoru nebo dolů číselné měřítko.
Výchozí hodnota je 0,0.
ChiSquare
Rozdělení chí-kvadrát je součet čtverců k nezávislých, standardních, normálních, náhodných proměnných.
Pokud chcete vypočítat, vyberte ChiSquare a nastavte následující možnosti:
- Počet stupňů volnosti Zadejte číslo (
double) pro určení stupňů volnosti. Výchozí hodnota je 1,0.
ChiSquareRightTailed
Tato možnost poskytuje rozdělení chí-kvadrát pravého chí-kvadrátu.
Pokud chcete vypočítat, vyberte ChiSquareRightTailed a nastavte následující možnosti:
- Počet stupňů volnosti
Zadejte číslo (double) pro určení stupňů volnosti. Výchozí hodnota je 1,0.
Exponenciální
Exponenciální rozdělení je rozdělení nad skutečnými čísly parametrizovaný jedním nezáporovým parametrem.
Výpočet provedete tak, že vyberete Exponenciální hodnotu a nastavíte následující možnosti:
- Lambda
Zadejte číslo (double), které chcete použít jako parametr lambda. Výchozí hodnota je 1,0.
FFisher
Vygeneruje pravděpodobnost fisherové statistiky pro vzorek, označovaný také jako Fisher F-distribution. Toto rozdělení je dvoustranné.
Pokud chcete vypočítat, vyberte FFisher a nastavte následující možnosti:
Stupně volnosti numerátoru
Zadejte číslo (double) pro určení stupňů volnosti, které se používají v čitatelu. Výchozí hodnota je 3.0.Stupně volnosti jmenovatele
Zadejte číslo (double) pro určení stupňů volnosti, které se používají ve jmenovateli. Výchozí hodnota je 6.0.
FFisherRightTailed
Vytvoří pravou chvost fisherova rozdělení. Fisherovo rozdělení se také označuje jako fisherová distribuce F-distribution, Snedecor rozdělení nebo Fisher-Snedecor rozdělení. Tato konkrétní forma rozdělení je pravá.
Pokud chcete vypočítat, vyberte FFisherRightTailed a nastavte následující možnosti:
Stupně volnosti numerátoru
Zadejte číslo (double) pro určení stupňů volnosti, které se používají v čitatelu. Výchozí hodnota je 3.0.Stupně volnosti jmenovatele
Zadejte číslo (double) pro určení stupňů volnosti, které se používají ve jmenovateli. Výchozí hodnota je 6.0.
Gama
Gama rozdělení je řada průběžných rozdělení pravděpodobností se dvěma parametry. Například chí-kvadrát je zvláštní případ gama rozdělení.
Pokud chcete vypočítat, vyberte gamma a nastavte následující možnosti:
Škálování
Zadejte hodnotu, kterou chcete použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Umístění
Zadejte číslo (double), které představuje umístění 0. elementu.Zadáním hodnoty parametru Location můžete posunout rozdělení pravděpodobnosti nahoru nebo dolů číselné měřítko.
Výchozí hodnota je 0,0.
GeneralizedExtremeValues
Vytvoří distribuci vyvinutou pro zpracování extrémních hodnot. Generalizovaná extrémní hodnota (GEV) rozdělení je ve skutečnosti skupina průběžných rozdělení pravděpodobností, která kombinuje Gumbel, Fréchet a Weibull rozdělení (označované také jako typ I, II a III extrémní rozdělení hodnot).
Další informace o extrémní teorii hodnot naleznete v tomto článku na Wikipedii: Fisher-Tippet-Gnedenko theorem.
Chcete-li vypočítat, vyberte GeneralizedExtremeValues a nastavte následující možnosti:
Obrazec
Zadejte hodnotu, která změní tvar rozdělení.Parametr obrazce je libovolný parametr rozdělení pravděpodobnosti, který nedefinuje jeho umístění nebo měřítko. Proto když zadáte hodnotu obrazce, parametr změní tvar rozdělení místo přesunutí, roztažení nebo zmenšení.
Hodnota musí být číslo (
double). Výchozí hodnota je 1,0.Škálování
Zadejte hodnotu, kterou chcete použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Umístění
Zadejte číslo (double), které představuje umístění 0. elementu.Zadáním hodnoty parametru Location můžete posunout rozdělení pravděpodobnosti nahoru nebo dolů číselné měřítko.
Výchozí hodnota je 0,0.
Geometrické
Geometrické rozdělení je rozdělení nad kladné celé číslo parametrizované jedním kladným skutečným číslem.
Pokud chcete vypočítat, vyberte Geometrický a nastavte následující možnosti:
- Pravděpodobnost úspěchu
Zadejte číslo (float) mezi 0,0 a 1,0, které označuje pravděpodobnost úspěchu. Výchozí hodnota je .5.
Poznámka
Tato implementace geometrického rozdělení negeneruje nuly.
GumbelMax
Gumbel rozdělení je jedním z několika extrémních hodnot rozdělení. Možnost GumbelMax implementuje distribuci Typu 1 maximální extrémní hodnoty.
Pokud chcete vypočítat, vyberte GumbelMax a nastavte následující možnosti:
Škálování
Zadejte hodnotu, kterou chcete použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Umístění
Zadejte číslo (double), které představuje umístění 0. elementu.Zadáním hodnoty parametru Location můžete posunout rozdělení pravděpodobnosti nahoru nebo dolů číselné měřítko.
Výchozí hodnota je 0,0.
GumbelMin
Gumbel rozdělení je jedním z několika extrémních hodnot rozdělení. Rozdělení Gumbel je také označováno jako nejmenší extrémní hodnota (SEV) rozdělení nebo nejmenší extrémní hodnota (Typ I). Možnost GumbelMin implementuje distribuci typu minimální extrémní hodnoty 1.
Pokud chcete vypočítat, vyberte GumbelMin a musíte nastavit následující možnosti:
Škálování
Zadejte hodnotu, kterou chcete použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Umístění
Zadejte číslo (double), které představuje umístění 0. elementu.Zadáním hodnoty parametru Location můžete posunout rozdělení pravděpodobnosti nahoru nebo dolů číselné měřítko.
Výchozí hodnota je 0,0.
Hypergeometrické
Hypergeometrické rozdělení je diskrétní rozdělení pravděpodobnosti, které popisuje počet úspěchů v sekvenci n načítá z konečné populace bez nahrazení, stejně jako binomické rozdělení popisuje počet úspěchů pro tahy s nahrazením.
Pokud chcete vypočítat, vyberte Hypergeometric a nastavte následující možnosti:
Počet vzorků
Zadejte celé číslo, které označuje počet vzorků, které se mají použít. Výchozí hodnota je 9.Počet úspěchů
Zadejte celé číslo, které definuje hodnotu pro úspěch. Výchozí hodnota je 24.Velikost populace
Zadejte velikost základního souboru, která se má použít při odhadu hypergeometrického rozdělení.
Laplaceova
Laplace rozdělení je rozdělení nad skutečnými čísly, parametrizované průměrem a parametrem škálování.
Pokud chcete vypočítat, vyberte laplace rozdělení a nastavte následující možnosti:
Škálování
Zadejte hodnotu, kterou chcete použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Umístění
Zadejte číslo (double), které představuje umístění 0. elementu.Zadáním hodnoty parametru Location můžete posunout rozdělení pravděpodobnosti nahoru nebo dolů číselné měřítko.
Výchozí hodnota je 0,0.
Logistické
Logistická distribuce je podobná normálnímu rozdělení, ale nemá žádné omezení na levé straně rozdělení. Logistická distribuce se používá v modelech logistické regrese a neurální sítě a pro modelování dat o životních vědách.
Pokud chcete vypočítat, vyberte Logistickou a nastavte následující možnosti:
Škálování
Zadejte hodnotu, kterou chcete použít pro škálování distribuce.Použitím hodnoty měřítka pro distribuci ji můžete zmenšit nebo roztáhnout.
Výchozí hodnota je 1,0. Hodnoty musí být kladná čísla.
Znamená
Zadejte číslo (double), které označuje odhadovanou průměrnou hodnotu rozdělení. Výchozí hodnota je 0,0.
Logaritmicko-normální
Logaritmické rozdělení je souvislé jednovariátové rozdělení.
Chcete-li vypočítat, vyberte Lognormal a nastavte následující možnosti:
Znamená
Zadejte číslo (double), které označuje odhadovanou průměrnou hodnotu rozdělení. Výchozí hodnota je 0,0.Směrodatná odchylka
Zadejte kladné číslo (double), které označuje odhadovanou směrodatnou odchylku rozdělení. Výchozí hodnota je 1,0.
NegativeBinomial
Negativní binomické rozdělení je rozdělení nad přirozenými čísly se dvěma parametry (r, p). V případě, že r se jedná o celé číslo, můžete rozdělení interpretovat jako počet chvostů předr. hlavou, pokud je pravděpodobnost hlavy p.
Pokud chcete vypočítat, vyberte NegativeBinomial a nastavte následující možnosti:
Pravděpodobnost úspěchu
Zadejte číslo (float) mezi 0,0 a 1,0, které označuje pravděpodobnost úspěchu. Výchozí hodnota je .5.Počet úspěchů
Zadejte celé číslo, které určuje hodnotu úspěchu. Výchozí hodnota je 24.
Normální
Normální rozdělení se také označuje jako gaussovské rozdělení.
Pokud chcete vypočítat, vyberte Normální a nastavte následující možnosti:
Znamená
Zadejte číslo (double), které označuje odhadovanou střední hodnotu rozdělení. Výchozí hodnota je 0,0.Směrodatná odchylka
Zadejte kladné číslo (double), které označuje odhadovanou směrodatnou odchylku rozdělení. Výchozí hodnota je 1,0.
Pareto
Paretovo rozdělení je rozdělení pravděpodobnosti mocninného práva, které se shoduje se sociálními, vědeckými, geofyzickými, aktuarialy a mnoha dalšími typy pozorovatelných jevů.
Pokud chcete vypočítat, vyberte Pareto a nastavte následující možnosti:
Obrazec
Zadejte hodnotu (volitelné) pro změnu tvaru rozdělení.Parametr obrazce je libovolný parametr rozdělení pravděpodobnosti, který nedefinuje jeho umístění ani měřítko. Proto když zadáte hodnotu obrazce, parametr změní tvar rozdělení místo přesunutí, roztažení nebo zmenšení.
Hodnota musí být číslo (
double). Výchozí hodnota je 1,0.Škálování
Zadejte hodnotu (volitelné) pro změnu měřítka rozdělení. Použitím hodnoty škálování na distribuci ji můžete zmenšit nebo roztáhnout.Hodnota musí být číslo (
double). Výchozí hodnota je 1,0.
Poisson
V této implementaci se metoda Knuth používá ke generování náhodných proměnných Poissona. Další informace o distribuci Poisson naleznete v tématu Poisson Regression.
Pokud chcete vypočítat, vyberte Poisson a nastavte následující možnosti:
- Znamená
Zadejte číslo (double), které označuje odhadovanou střední hodnotu rozdělení. Výchozí hodnota je 0,0.
Rayleigh
Rayleighovo rozdělení je průběžné rozdělení pravděpodobnosti. Jako příklad toho, jak to vznikne, rychlost větru bude mít rozdělení Rayleigh, pokud součásti dvojrozměrného vektoru rychlosti větru nesouvisejí a obvykle distribuují se stejnou odchylkou.
Pokud chcete vypočítat, vyberte Rayleigh a nastavte následující možnosti:
- Dolní mez
Zadejte číslo (double), které představuje dolní mez rozdělení. Výchozí hodnota je 0,0.
StandardNormal
Tato možnost poskytuje standardní normální rozdělení bez dalších parametrů.
Chcete-li vypočítat, vyberte StandardNormal a vyberte sloupce.
TStudent
Tato možnost implementuje univariát studentova t-rozdělení.
Pokud chcete vypočítat, vyberte TStudent a nastavte následující možnosti:
- Počet stupňů volnosti
Zadejte číslo (double) k určení stupňů volnosti. Výchozí hodnota je 1,0.
TStudentRightTailed
Implementuje jednovariátní studentovo t-rozdělení pomocí jednoho pravého chvostu.
Pokud chcete vypočítat, vyberte TStudentRightTailed a nastavte následující možnosti:
- Počet stupňů volnosti
Zadejte číslo (double) k určení stupňů volnosti. Výchozí hodnota je 1,0.
TStudentTwoTailed
Implementuje dvojstranné studentovo t-rozdělení.
Pokud chcete vypočítat, vyberte TStudentTwoTailed a nastavte následující možnosti:
- Počet stupňů volnosti
Zadejte číslo (double) k určení stupňů volnosti. Výchozí hodnota je 1,0.
Jednotné
Rovnoměrné rozdělení se také označuje jako obdélníkové rozdělení.
Pokud chcete vypočítat, vyberte Uniform (Uniform) a nastavte následující možnosti:
Dolní mez
Zadejte číslo (double), které představuje dolní limit rozdělení. Výchozí hodnota je 0,0.Horní mez
Zadejte číslo (double), které představuje horní limit rozdělení. Výchozí hodnota je 1,0.
Weibull
Weibull distribuce je široce používána ve spolehlivosti inženýrství. Pomocí parametru Shape můžete modelovat mnoho dalších distribucí.
Pokud chcete vypočítat, vyberte Weibull a nastavte následující možnosti:
Obrazec
Zadejte hodnotu (volitelné) pro změnu tvaru rozdělení.Parametr obrazce je libovolný parametr rozdělení pravděpodobnosti, který nedefinuje jeho umístění ani měřítko. Proto když zadáte hodnotu obrazce, parametr změní tvar rozdělení místo přesunutí, roztažení nebo zmenšení.
Hodnota musí být číslo (
double). Výchozí hodnota je 1,0.Škálování
Zadejte hodnotu (volitelné) pro změnu měřítka rozdělení. Použitím hodnoty škálování na distribuci ji můžete zmenšit nebo roztáhnout.Hodnota musí být číslo (
double). Výchozí hodnota je 1,0.
Technické poznámky
Tato část obsahuje podrobnosti o implementaci, tipy a odpovědi na nejčastější dotazy.
Podrobnosti o implementaci
Tento modul podporuje všechny distribuce poskytované v knihovně open source MATH.NET Numerics. Další informace najdete v dokumentaci k knihovně Math.Net.Numerics.Distribution .
Pravá a dvoustranná rozdělení se zobrazují jako samostatná rozdělení, nikoli jako parametrizované verze základních distribucí. Aktuální chování spočívá v zachování kompatibility s Excel.
Definice
Tento modul podporuje výpočet kterékoli z těchto hodnot pro zadanou distribuci:
cdf nebo kumulativní distribuční funkce
Vrátí pravděpodobnost složené události definované jako součetcurrences, když náhodná proměnná vezme hodnotu menší než určitá hodnota x.
Jinými slovy, odpovídá na otázku: "Jak běžné jsou vzorky, které jsou menší než nebo rovno této hodnotě?"
Tuto funkci lze použít s průběžnými i diskrétními číselnými proměnnými.
InverseCdf nebo inverzní kumulativní distribuční funkce
Vrátí hodnotu přidruženou ke konkrétní kumulativní hodnotě pravděpodobnosti (cdf).
Jinými slovy, odpoví na otázku: "Jaká je hodnota x, při které funkce cdf vrátí kumulativní pravděpodobnost y?"
pdf nebo funkce hustoty pravděpodobnosti
Popisuje relativní pravděpodobnost, že náhodná proměnná bude konkrétní hodnotou.
Jinými slovy, odpovídá na otázku: "Jak běžné jsou vzorky přesně v této hodnotě?"
Očekávané vstupy
| Název | Typ | Description |
|---|---|---|
| Datová sada | Tabulka dat | Vstupní datová sada |
Parametry modulu
| Name | Rozsah | Typ | Výchozí | Description |
|---|---|---|---|---|
| Distribuce | Všechny | PravděpodobnostiDistribution | StandardNormal | Vyberte druh rozdělení pravděpodobnosti, který chcete vygenerovat. |
| Metoda | Všechny | PravděpodobnostDistributionMethod | Cdf | Vyberte metodu, která se má použít při výpočtu vybraného rozdělení pravděpodobnosti. Možnosti jsou kumulativní distribuční funkce (cdf), inverzní kumulativní distribuční funkce (InverseCdf) a funkce hustoty pravděpodobnosti nebo hromadná funkce (PDF). |
| Záporná binomická metoda distribuce | Všechny | PravděpodobnostDistributionMethodForNegativeBinomial | Cdf | Pokud vyberete negativní binomické rozdělení, zadejte metodu použitou k vyhodnocení rozdělení. |
| Pravděpodobnost úspěchu | [0.0;1.0] | Float | 0,5 | Zadejte hodnotu, která se má použít jako pravděpodobnost úspěchu. |
| Tvar | Všechny | Float | 1.0 | Zadejte hodnotu, která upraví tvar rozdělení. |
| Měřítko | >=0,0 | Float | 1.0 | Zadejte hodnotu, která změní měřítko distribuce, aby se rozbalil nebo zmenšil. |
| Počet pokusů | >=1 | Integer | 3 | Zadejte počet pokusů. |
| Dolní mez | Všechny | Float | 0,0 | Zadejte číslo, které chcete použít jako dolní limit rozdělení. |
| Horní mez | Všechny | Float | 1.0 | Zadejte číslo, které chcete použít jako horní mez rozdělení. |
| Umístění | Všechny | Float | 0,0 | Zadejte umístění nulového prvku v rozdělení. |
| Počet stupňů volnosti | Všechny | Float | 1.0 | Zadejte počet stupňů volnosti. |
| Stupně volnosti numerátoru | Všechny | Float | 3.0 | Zadejte počet stupňů volnosti v čitatelu. |
| Stupně volnosti jmenovatele | Všechny | Float | 6.0 | Zadejte počet stupňů volnosti ve jmenovateli. |
| Lambda | >=0,0 | Float | 1.0 | Zadejte hodnotu parametru Lambda. |
| Počet vzorků | Všechny | Integer | 9 | Zadejte počet vzorků. |
| Počet úspěchů | Všechny | Integer | 24 | Zadejte hodnotu, která se má použít jako počet úspěchů. |
| Velikost populace | Všechny | Integer | 52 | Zadejte velikost základního souboru. |
| Mean | Všechny | Float | 0,0 | Zadejte odhadovanou střední hodnotu. |
| Směrodatná odchylka | >=0,0 | Float | 1.0 | Zadejte odhadovanou směrodatnou odchylku. |
| Sada sloupců | Všechny | ColumnSelection | Vyberte sloupce, u kterých se má vypočítat rozdělení pravděpodobnosti. | |
| Režim výsledků | Všechny | OutputTo | ResultOnly | Určete, jak se mají výsledky uložit do výstupní datové sady. Možnosti jsou přidávat nové sloupce, nahradit existující sloupce nebo výstup pouze výsledky. |
Výstup
| Název | Typ | Description |
|---|---|---|
| Datová sada výsledků | Tabulka dat | Výstupní datová sada |
Výjimka
Úplný seznam chybových zpráv najdete v tématu Kódy chyb modulu.
| Výjimka | Description |
|---|---|
| Chyba 0017 | K výjimce dochází v případě, že jeden nebo více zadaných sloupců má typ, který aktuální modul nepodporuje. |
Seznam chyb specifických pro moduly Studio (Classic) najdete v tématu Machine Learning Kódy chyb.
Seznam výjimek rozhraní API najdete v tématu Machine Learning kódy chyb rozhraní REST API.