附錄:矩陣轉換
本主題提供 2D 圖形矩陣轉換的數學概觀。 不過,您不需要知道矩陣數學,才能在 Direct2D 中使用轉換。 如果您對數學感興趣,請閱讀本主題;否則,請放心略過本主題。
矩陣簡介
矩陣是實數的矩形陣組。 矩陣 順序 是數據列和數據行數目。 例如,如果矩陣有 3 個資料列和 2 個數據行,則順序為 3 × 2。 矩陣通常會以方括弧括住的矩陣元素來顯示:
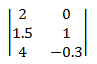
表示法:矩陣是由大寫字母指定。 元素是由小寫字母所指定。 下標表示項目的數據列和數據行編號。 例如,ij 是矩陣 A 的第 i 列和第 j 欄的專案。
下圖顯示 i × j 矩陣,其中包含矩陣中每個儲存格中的個別元素。

矩陣作業
本節描述在矩陣上定義的基本作業。
新增。 藉由新增 A 和 B 的對應元素,可取得兩個矩陣的總和 A + B:
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
純量乘法。 此作業會將矩陣乘以實數。 假設實數 k,純量乘積 kA 會乘以 A 的每個元素乘以 k。
- kA = k\[ a*ij* \] = \[ k × a*ij* \]
矩陣乘法。 假設有兩個矩陣 A 和 B 與 order (m × n) 和 (n × p), 產品 C = A × B 是具有訂單的矩陣 (m × p),定義為如下:
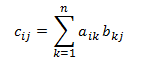
或者,同樣地:
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*
也就是說,若要計算每個元素 cij,請執行下列動作:
- 取得 A 的第一個數據列和 B 的 j『th 數據行。
- 將數據列和數據行中的每個專案組相乘:第一個數據列專案乘以第一個數據行專案、第二列專案乘以第二個數據行專案等等。
- 加總結果。
以下是將 (2 × 2) 矩陣乘以 (2 × 3) 矩陣的範例。
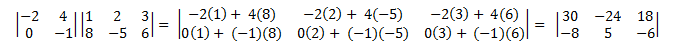
矩陣乘法不是通勤的。 也就是說,A × B ≠ B × A。此外,從其之後的定義中,並非所有矩陣都可以相乘。 左側矩陣中的數據行數目必須等於右側矩陣中的數據列數目。 否則,不會定義×運算符。
識別矩陣。 指定 I 的識別矩陣是定義如下的平方矩陣:
- I*ij* = 1 如果 *i* = *j*,否則為 0。
換句話說,識別矩陣會針對每個元素包含1,其中數據列編號等於數據行編號,而所有其他元素則為零。 例如,以下是 3 × 3 個識別矩陣。
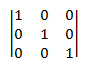
任何矩陣 M 的下列相等性保留。
- M x I = M I x M = M
Affine Transforms
仿射轉換 是一種數學運算,可將一個座標空間對應到另一個座標空間。 換句話說,它會將一組點對應到另一組點。 Affine 轉換具有一些功能,讓它們在計算機圖形中很有用。
- Affine 轉換會保留 合數。 如果三個以上的點落在一行上,它們仍然會在轉換后形成一條線。 直線保持直線。
- 兩個相合轉換的組成是仿射轉換。
2D 空間的 Affine 轉換具有下列形式。
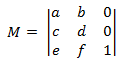
如果您稍早套用矩陣乘法的定義,您可以顯示兩個相合轉換的乘積是另一個仿射轉換。 若要使用仿射轉換來轉換 2D 點,該點會以 1 × 3 矩陣表示。
- P = \|x y 1 \|
前兩個元素包含點的 x 和 y 座標。 1 會放在第三個元素中,讓數學正確運作。 若要套用轉換,請將兩個矩陣相乘,如下所示。
- P' = P × M
這會展開至下列內容。
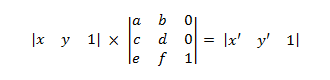
哪裡
- x' = ax + cy + e y' = bx + dy + f
若要取得轉換的點,請取得矩陣 P' 的前兩個元素。
- p = (x', y') = (ax + cy + e, bx + dy + f)
注意
1 × n 矩陣稱為 資料列向量。 Direct2D 和 Direct3D 都使用數據列向量來表示 2D 或 3D 空間中的點。 您可以使用資料行向量 (n × 1) 並轉置轉換矩陣來取得相等的結果。 大部分的圖形文字都會使用數據行向量形式。 本主題提供數據列向量表單,以符合 Direct2D 和 Direct3D 的一致性。
接下來的數個區段衍生基本轉換。
翻譯轉換
轉譯轉換矩陣的格式如下。
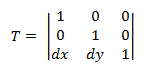
將點插入 P 這個方程式會產生:
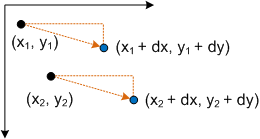
- P' = (*x* + *dx*, *y* + *dy*)
會對應到 X 軸中 dx 所翻譯的點 (x, y), Y 軸中的 dy。
調整轉換
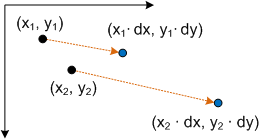
縮放轉換矩陣的格式如下。
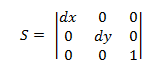
將點插入 P 這個方程式會產生:
- P' = (*x* ≦ *dx*, *y* ≦ *dy*)
,對應到以 dx 和 dy縮放的點 (x,y)。
繞原點旋轉
要繞原點旋轉的矩陣具有下列形式。
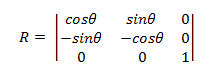
轉換的點為:
- P' = (*x*cos***– ysin^, *x*sin^+ *y*cos^)
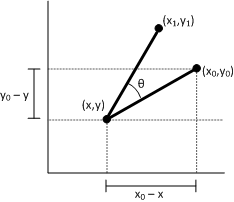
證明。 若要顯示 P 代表旋轉,請考慮下圖。
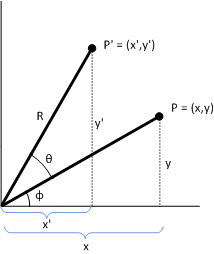
鑒於:
-
P = (x,y)
-
要轉換的原始點。
-
Φ
-
線條 (0,0) 到 P 所形成的角度。
-
Θ
-
旋轉原點的角度(x,y)。
-
P' = (x',y')
-
已轉換的點。
-
R
-
行 (0,0) 到 P 的長度。此外,旋轉圓形的半徑。
注意
此圖表使用幾何中使用的標準座標系統,其中正 y 軸向上點。 Direct2D 使用 Windows 座標系統,其中正 y 軸向下點。
X 軸與線條 (0,0) 到 P' 之間的角度為 Ф + Ф。 下列身分識別保留:
- x = R cosФ y = R sinФ x' = R cos(Ф + Ф) y' = R sin(Ф+ Ф)
現在,針對 X' 和 y' 解決 ^。 透過三角加法公式:
- x' = R(cosФcosФ – sinФsinФ) = RcosФcosФ – RsinФsinФ y' = R(sinФcosФ + cosInФ) = RsinФcosФ + RcosФsinФ
我們得到:
- x' = xcos≦– ysin^y' = xsin+++ ycos≦
,對應到稍早顯示的轉換點 P。
繞著任意點旋轉
若要繞著原點以外的點 (x,y) 旋轉,則會使用下列矩陣。
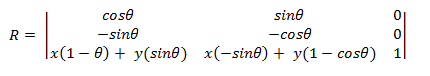
您可以將點 (x,y) 設為原點來衍生此矩陣。
Let (x1, y1) 是旋轉點 (x0, y0) 繞點 (x,y) 所產生的點 (x,y1)。 我們可以衍生 x1,如下所示。
- x1 = (x0 – x)cos^– (y0 – y)sin^+ x x1 = x0cos Ctrl – y0sin^+ \[ (1 – cosN) + ysin^]
現在,使用公式 x1 = ax0 + cy0 + e 從稍早插入轉換矩陣。 使用相同的程式來衍生 y1。
扭曲轉換
扭曲轉換是由四個參數所定義:
- 1:沿著 X 軸扭曲的數量,以 Y 軸的角度測量。
- Ф:沿著 Y 軸扭曲的數量,以 X 軸的角度測量。
- (px,py):執行扭曲之點的 x 和 y 座標。
扭曲轉換會使用下列矩陣。
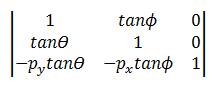
轉換的點為:
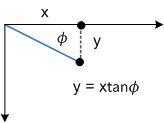
- P' = (*x* + *y*tanФ – *py*tanФ, *y* + *x*tanФ) – *py*tanФ
或對等方式:
- P' = (*x* + (*y* – *py*)tanФ, *y* + (*x* – *px*)tanФ)
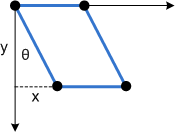
若要查看此轉換的運作方式,請個別考慮每個元件。 ≦參數會將 x 方向中的每個點移動等於 tan^。 下圖顯示 ^與 x 軸扭曲之間的關聯性。
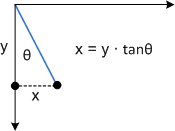
以下是套用至矩形的相同扭曲:
Ф 參數的效果相同,但沿著 Y 軸:
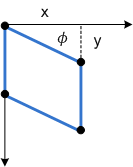
下圖顯示套用至矩形的 Y 軸扭曲。
最後,參數 px,py 沿著 x 軸和 y 軸移動扭曲的中心點。
代表 Direct2D 中的轉換
所有 Direct2D 轉換都是仿射轉換。 Direct2D 不支援非仿射轉換。 轉換是由 D2D1_MATRIX_3X2_F 結構表示。 此結構會定義 3 × 2 矩陣。 由於 affine 轉換的第三個數據行一律相同 ([0, 0, 1]),而且因為 Direct2D 不支援非仿射轉換,因此不需要指定整個 3 × 3 矩陣。 在內部,Direct2D 會使用 3 × 3 個矩陣來計算轉換。
D2D1_MATRIX_3X2_F 的成員會根據其索引位置來命名:_11 成員是元素 (1,1),_12 成員是元素 (1,2),依此類推。 雖然您可以直接初始化結構成員,但建議您使用 D2D1::Matrix3x2F 類別。 這個類別會繼承 D2D1_MATRIX_3X2_F,並提供協助程式方法來建立任何基本的仿射轉換。 類別也會定義 運算符*() 來撰寫兩個或多個轉換,如在 Direct2D 中套用轉換中所述。
下一個