旋轉色彩

四維色彩空間中的旋轉很難視覺化。 我們可以藉由同意讓其中一個色彩元件保持固定，讓旋轉更容易視覺化。 假設我們同意將 Alpha 元件固定在 1 (完全不透明) 。 然後，我們可以視覺化具有紅色、綠色和藍色座標軸的三維色彩空間，如下圖所示。

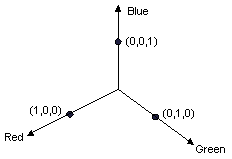
色彩可以視為立體空間中的點。 例如，空間中的點 (1、0、0) 代表紅色，而空間中的點 (0、1、0) 代表綠色。

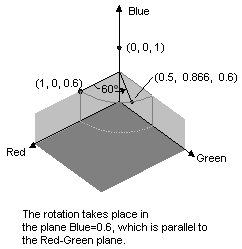
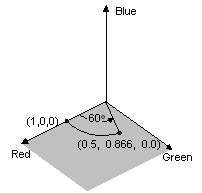
下圖顯示 (1、0、0) 旋轉Red-Green平面中 60 度角度的色彩的意義。 平行于Red-Green平面的旋轉可以視為藍色軸的旋轉。

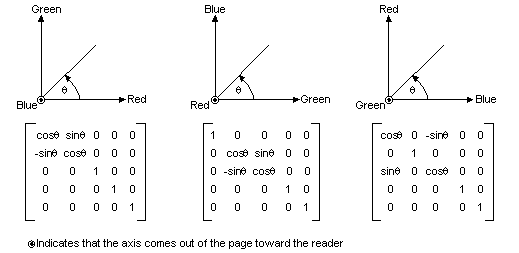
下圖顯示如何初始化色彩矩陣，以執行三個座標軸的旋轉 (紅色、綠色、藍色) 。

下列範例會採用一個影像，該影像全都是一個色彩 (1、0、0.6) ，並套用 60 度旋轉的藍色軸。 旋轉的角度會在與Red-Green平面平行的平面中清除。

Image            image(L"RotationInput.bmp");
ImageAttributes  imageAttributes;
UINT             width = image.GetWidth();
UINT             height = image.GetHeight();
REAL             degrees = 60;
REAL             pi = acos(-1);  // the angle whose cosine is -1.
REAL             r = degrees * pi / 180;  // degrees to radians

ColorMatrix colorMatrix = {
   cos(r),  sin(r), 0.0f, 0.0f, 0.0f,
   -sin(r), cos(r), 0.0f, 0.0f, 0.0f,
   0.0f,    0.0f,   1.0f, 0.0f, 0.0f,
   0.0f,    0.0f,   0.0f, 1.0f, 0.0f,
   0.0f,    0.0f,   0.0f, 0.0f, 1.0f};
   
imageAttributes.SetColorMatrix(
   &colorMatrix, 
   ColorMatrixFlagsDefault,
   ColorAdjustTypeBitmap);
   
graphics.DrawImage(&image, 10, 10, width, height);

graphics.DrawImage(
   &image, 
   Rect(130, 10, width, height),  // destination rectangle 
   0, 0,        // upper-left corner of source rectangle 
   width,       // width of source rectangle
   height,      // height of source rectangle
   UnitPixel,
   &imageAttributes);

下圖顯示左側的原始影像，以及右邊的色彩旋轉影像。

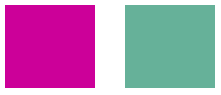
上述程式碼範例中執行的色彩旋轉可以視覺化，如下所示。