參數曲線
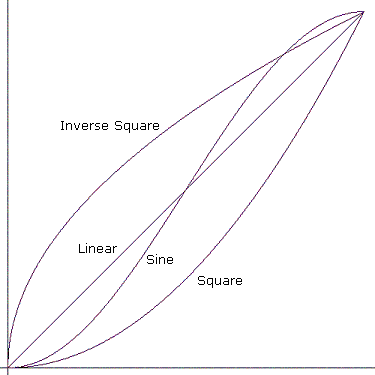
媒體參數可以追蹤一段時間的曲線。 每個曲線都是由數學公式和兩個端點來描述。 每個端點都是由參考時間和該時間曲線的值所定義。 公式可用來計算點之間的中繼值,並決定曲線的形狀。 可能的曲線如下:
- 跳
- 線性
- Square
- 反正方形
- 正弦函數
「Jump」 表示直接跳到結束值。 下圖顯示其他曲線。
以數學方式,曲線的運作方式如下。 假設曲線從 時間 t₀ 開始,值為 v₀,並在 t₁ 時結束 ,值為 v₁。 定義曲線的兩個點 (t₀、v₀) 和 (t₁ v₁) 。
- 讓 Еt 是曲線的總持續時間 ,t₁–t₀。
- 讓 ーv 是開始和結束值 v₁–v₀ 之間的間隔。
- 每當t₀ < = t= t< ₁,let ー t' = t–t₀。
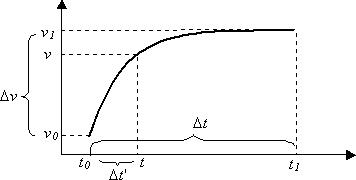
參數在時間 t 的值為:
v = f ( (t'/ ー + t ) *v₀
其中 f (x) 是由曲線類型決定的函式:
- 線性:y = x
- 方形:y = x^2
- 反正方形:y = sqrt (x)
- 正弦值:y = [ sin (πx – π/2) + 1 ] / 2
觀察T' <顯示,因此字詞 其範圍從 0 到 1。 因此,f (x) 範圍也介於 0 到 1 之間, 而 v 一律介於 v₀ 和 v₁之間。 不論v₀ <v₁ 或反之亦然,都是如此。 換句話說,曲線是由矩形系結, (t₀、 v₀、 t₁、 v₁) 。
針對正弦曲線, (πx – π/2 的值) 範圍從 –π/2 到 π/2,這表示 sin (πx – π/2) 範圍從 –1 到 1。 結果接著會正規化,讓 f (x) 落在 0-1) 的範圍 (。
相關主題