PRT 方程式 （Direct3D 9）

若要完全了解實作 PRT 的著色器，衍生著色器用來計算結束輻射的公式很有用。

若要開始，下列方程式是一般方程式，用來計算在具有任意遠距離光源的擴散物件上直接光源所產生的結束輻射度。

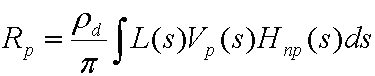
哪裡：

參數	描述
Rp	頂點 p 的結束弧度。 在網格的每個頂點上評估。
pd	表面的 albedo。
圓周率	常數，用來作為節能正規化因數。
L（s）	光源環境（來源輻射）。
Vp₍s₎	點 p 的二進位可見性函式。 如果點可以看到光線，則為 1，如果不是，則為 0。
Hnp₍s₎	蘭伯特法律中的餘弦詞彙。 等於 max（Np• s）， 0）， 其中 Np 是點 p 的正常表面。
s	在球體上整合的變數。

 

使用球面基礎函式，例如球面調和，下列方程式會近似光源環境。

光源環境的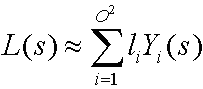

哪裡：

參數	描述
L（s）	光源環境（來源輻射）。
我	整數，會加總基礎函式的數目。
O	球面調和的順序。
li	係數。
Yi（s）	球體上的一些基礎函式。

 

這些係數的集合 L'，為函式 L（s） 提供基數函式 Y（s） 的最佳近似值。 替代和散發會產生下列方程式。

在替代 l（s） 和分配方程式

Y_i（s）Vp₍s₎Hnp₍s₎ 是轉換係數 t_pi 仿真器針對網格上每個頂點預先計算的傳輸係數。 取代這個會產生下列方程式。

在替代轉移係數后，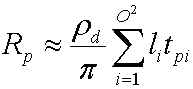

將此變更為向量表示法會產生下列未壓縮的方程式，以計算每個通道的結束弧度。

在變更為向量表示法之後，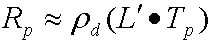

哪裡：

參數	描述
Rp	頂點 p 的結束弧度。
pd	表面的 albedo。
L'	li的向量，是將來源輻射投射到球面調和基數函式中的向量。 這是球面調和係數的順序 6 向量。
衛生紙	頂點 p 的順序 2012 轉送向量。 模擬器會將傳輸係數除以 p。

 

這兩個向量都是球面調和係數的順序，因此請注意，這隻是點乘積。 視順序而定，點可能很昂貴，因此可以使用壓縮。 稱為叢集主體元件分析 （CPCA） 的演算法會有效壓縮數據。 這可讓您使用高階球面調和近似值，進而產生更銳利的陰影。

CPCA 提供下列方程式來近似傳輸向量。

近似傳輸向量方程式

哪裡：

參數	描述
衛生紙	頂點 p 的傳輸向量。
Mk	叢集 k 的平均值。
j	整數，可加總 PCA 向量的數目。
N	PCA 向量的數目。
wpj	點 p 的第 jth PCA 權數。
Bkj	叢集 k 的第 jth PCA 基礎向量。

 

叢集只是共用相同平均向量的一些頂點。 以下將討論如何取得叢集平均數、PCA 權數、PCA 基礎向量，以及頂點的叢集標識符。

取代這兩個方程式會產生：

在替代轉移向量后，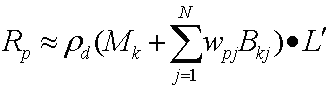

然後散發點乘積會產生下列方程式。

在散佈點產品

因為兩者 （Mk·L'） 和 （B_kj·L'） 是每個頂點的常數，範例會使用 CPU 計算這些值，並將其當做常數傳遞至頂點著色器：因為 w_pj 每個頂點的變更，因此範例會將這個每個頂點數據儲存在頂點緩衝區中。

相關主題

預先計算的輻射傳輸