多項式迴歸

  • 6 分鐘

到目前為止，我們只探討了線性迴歸模型，也就是可以模型化為直線的模型。 不過，迴歸模型可以與幾乎任何其他類型的關聯性搭配運作。

什麼是多項式迴歸？

多項式迴歸模型將關聯性模型化為特定的曲線類型。 多項式是一系列曲線，從簡單到複雜的圖形。 方程式的 (模型) 中的參數愈多，曲線就越複雜。

例如，雙參數多項式只是一條直線：

y = 截距 + B1*x

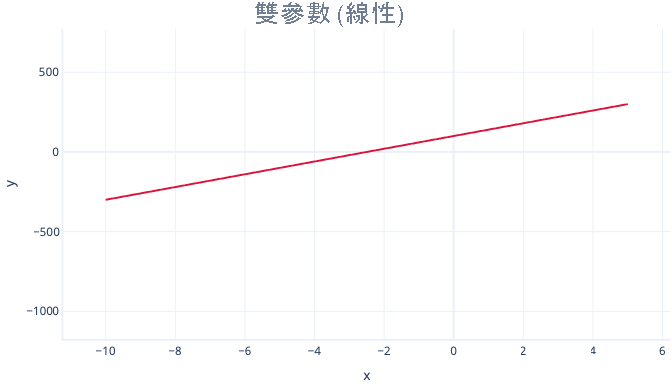
顯示雙參數多項式迴歸圖的圖表。

雖然三個參數多項式在其中有一個彎曲：

y = 截距 + B1*x + B2 * x2

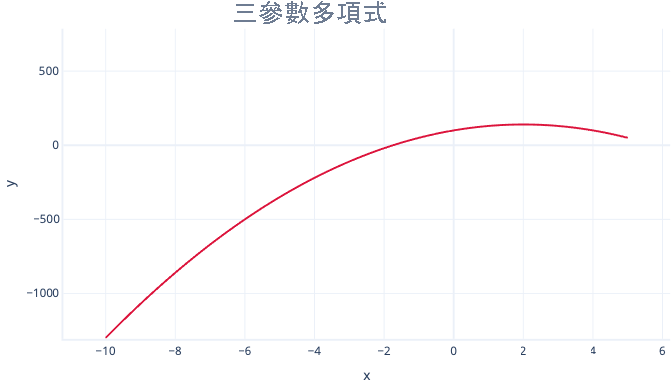
顯示三個參數多項式迴歸圖的圖表。

而且四個參數多項式可以有兩個彎曲：

y = 截距 + B1* x + B2 * x2 + B3 * x3

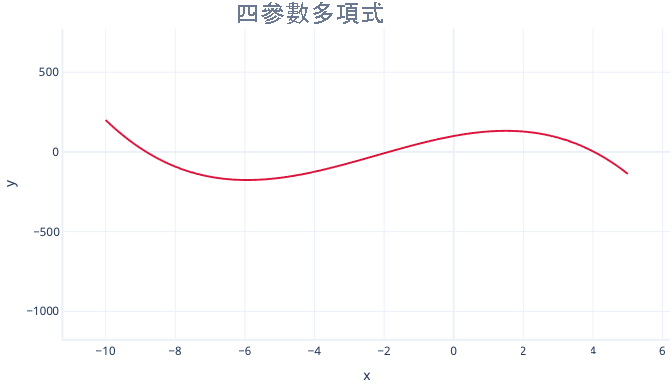
顯示四個參數多項式迴歸圖的圖表。

多項式與其他曲線

曲線有許多種，例如對數曲線和邏輯 (S 形) 曲線，都可以與迴歸一起使用。

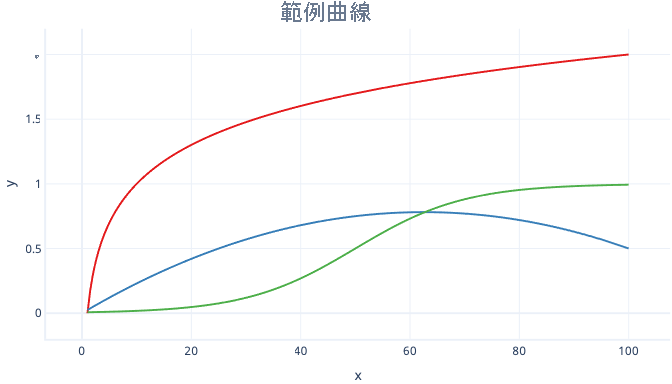
顯示多項式、對數和邏輯曲線的圖表。

多項式迴歸的主要優點是，可以用來查看各種關聯性。 例如，您可以使用多項式迴歸查看在特徵值特定範圍內為負數，但在其他範圍內是正數的關聯性。 也可以在標籤 (y 值) 沒有理論上限的情況下使用。

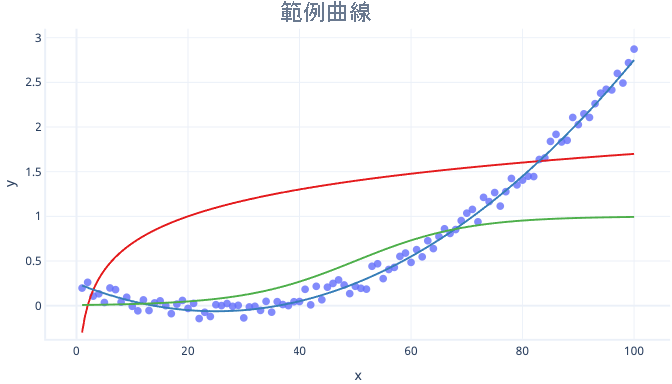
此圖顯示多項式曲線上具有繪圖點的多項式、對數和邏輯曲線。

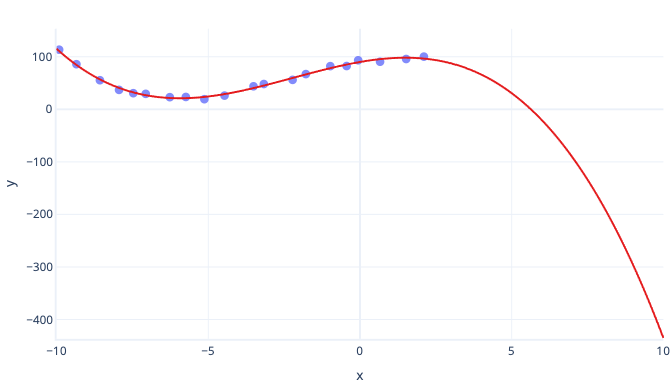
多項式曲線的主要缺點是其推斷通常不佳。 換句話說，如果我們嘗試預測比定型資料更大或更小的值，多項式可能會預測不切實際的極端值。 另一個缺點是，多項式曲線很容易過度擬合。 這表示資料中的雜訊比簡單的模型 (例如簡單線性迴歸)，更可以變更曲線的圖形。

顯示繪圖具有不正確多項式曲線的圖表。

曲線可以搭配多重特徵使用嗎？

我們已經看過多重迴歸可以同時符合數個線性關聯性的方式。 但是，不需要將這些限制為線性關聯性。 在適當的情況下，所有種類的曲線都可以用於這些關聯性。 不過，請小心不要在不需要的情況下，使用具有多個特徵的曲線 (例如多項式)。 這是因為關聯性最後可能會很複雜，因此難以理解模型，而且難以評估是否會做出從真實世界的觀點來看不合理的預測。