多重線性迴歸和 R 平方
在此單元中,我們將會使用「簡單線性迴歸」來對比多個線性迴歸。 我們也會查看名為 R2 的計量,此計量通常用來評估線性迴歸模型的品質。
多元線性迴歸
「多個線性迴歸」會將數個功能和一個變數之間的關聯性模型化。 在數學上,其與簡單線性迴歸相同,而且通常符合使用相同成本函式的功能,但有更多功能。
這項技術並不會將單一關聯性模型化,而是會同時將多個關聯性視為彼此獨立。 例如,如果我們想要根據預測狗的年齡和 body_fat_percentage 來預測狗的病情,則會發現兩個關聯性:
- 年齡如何增加或減少疾病
- Body_fat_percentage 如何增加或減少疾病
如果我們只使用兩個功能,我們可以將模型視覺化為平面對平面的 2D 介面,就像我們可以將簡單的線性迴歸模型化成為線條。 我們將會在下個練習中探討這項操作。
多重線性迴歸具有假設
模型預期功能會「獨立」的事實稱為模型假設。 當模型假設不是 true 時,模型可能會產生誤導的預測。
例如,年齡可能可以預測狗的病情,因為狗愈老愈會容易生病,以及是否教過狗如何玩飛盤:愈老的狗可能都知道如何玩飛盤。 如果在我們的模型中包含年齡和 knows_frisbee,就可能會告訴我們,如何玩飛盤是一項生病的良好預測指標,且低估了年齡的重要性。 這有點荒謬,因為知道玩飛盤不太可能會導致生病。 相較之下,dog_breed 也可能是個很好的生病預測指標,但是沒有理由可以預測狗的品種,因此在模型中包含這兩種方式會比較安全。
符合比例:R2
我們知道成本函式可以用來評估模型如何符合其定型的資料。 線性迴歸模型有一個稱為 R2 (「判定係數」) 的特殊相關量值。 R2 是介於 0 和 1 之間的值,可告訴我們線性迴歸模型與資料的相符程度。 當人們談論強式的相互關聯時,通常表示 R2 值很大。
R2 使用的數學超出我們在本課程中涵蓋的範圍,但我們可以憑直覺思考。 我們來看一下先前的練習,看看年齡與 core_temperature 之間的關聯性。 1 的 R2 表示年紀可以用來精確預測體溫較高和較低的人。 相反地,0 表示年紀和體溫之間沒有任何關聯性。
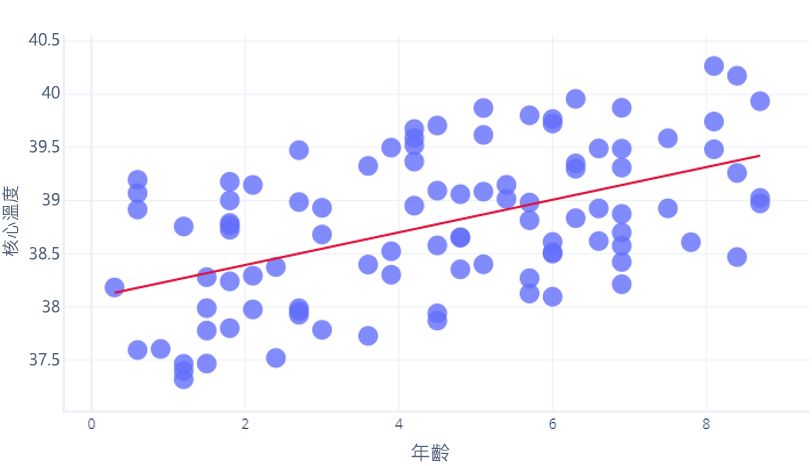
實際情況是在之間的某個地方。 我們的模型可以將溫度預測到某種程度 (因此比 R2 = 0 更好),但點與這種預測有所不同 (因此小於 R2=1)。
R2 只是故事的一半。
R2 值已被廣泛接受,但不是可用於隔離的完美量值。 其有四項限制:
- 由於 R2 的計算方式,我們擁有的樣本越多,R2 就愈高。 這可能會導致我們認為某個模型優於另一個 (相同) 模型,單純因為 R2 值是使用不同的資料量來計算。
- R2 值不會告訴我們,模型如何搭配先前未看見的新資料運作。 統計學家藉由計算補充量值,稱為 p 值,來克服此情況,這我們將不會在此討論。 在機器學習中,我們通常會改為在另一個資料集上明確地測試模型。
- R2 值不會告訴我們關聯性的方向。 例如,R2 值為0.8 時,不會告訴我們該線條是向上或向下的斜角。 此外,其也不會告訴我們該行的斜角程度。
也值得記住,針對 R2 值「非常好」而言,不存在通用的準則。例如,在大多數物理學當中,不太可能將非常近似 1 的相互關聯視為實用,但當模型化複雜系統時,R2 值若低於至 0.3 則可能被視為是絕佳的。