深度神經網路概念

  • 10 分鐘

在探索如何對深度神經網路 (DNN) 機器學習模型進行定型之前，請先考慮我們想嘗試實現的目標。 機器學習涉及根據特定觀察的某些「特徵」來預測「標籤」。 簡單來說，機器學習模型是一種函式，其會從 x (特徵) 計算 y (標籤)：f(x)=y。

簡單分類範例

例如，假設您的觀察包含企鵝的一些度量。

A penguin with a ruler and weighing scales

具體來說，度量是：

  • 企鵝喙的長度。
  • 企鵝喙的深度。
  • 企鵝鰭肢的長度。
  • 企鵝的重量。

在此情況下，特徵 (x) 是四個值的向量，以數學來表示的話，即為 x=[x1,x2,x3,x4]。

假設我們嘗試預測的標籤 (y) 是企鵝的物種，而且有三個可能的物種，分別為：

  1. 阿德利
  2. 「金圖企鵝」
  3. 「頰帶企鵝」

這是「分類」問題的範例，其中機器學習模型必須預測觀察最有可能屬於哪一個類別。 分類模型會透過預測由每個類別的機率所組成的標籤來完成此作業。 換句話說，y 是三個機率值的向量；每個可能的類別都有一個機率值：y=[P(0),P(1),P(2)]。

您可以使用您已經知道其真正標籤的觀察來為機器學習模型定型。 例如，您可能會有「阿德利」標本的下列特徵度量：

x=[37.3, 16.8, 19.2, 30.0]

您已知道這是「阿德利企鵝」(類別 0) 的範例，因此完美的分類函式所產生的標籤，應該要能指出類別 0 的機率為 100%，而類別 1 和 2 的機率為 0%：

y=[1, 0, 0]

深度神經網路模型

那麼，我們要如何使用深度學習來建置企鵝分類模型的分類模型？ 讓我們看看一個範例：

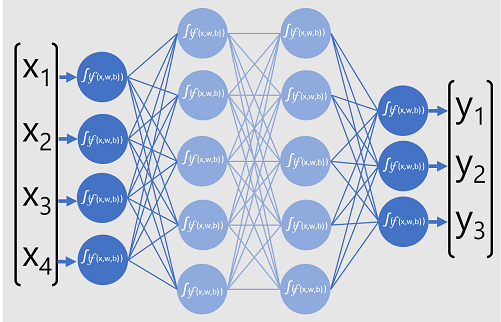
A neural network with four neurons in an input layer, two hidden layers, and three neurons in an output layer

分類器的深度神經網路模型是由多層人工神經元所組成。 在此案例中，一共有四層：

  • 一個「輸入」層，其中針對每個預期輸入 (x) 值都有一個神經元。
  • 兩個所謂的「隱藏」層，每層包含五個神經元。
  • 一個「輸出」層，其中包含三個神經元；模型要預測的每個類別機率 (y) 值都有一個神經元。

由於網路的分層架構，此類模型有時稱為「多層認知」。 此外，請注意，輸入層和隱藏層中的所有神經元都會連接到後續層中的所有神經元；這是「完全連線網路」的範例。

當建立像這樣的模型時，您必須定義一個輸入層，以支援您模型將處理的特徵數目；以及定義一個輸出層，以反映您預期模型會產生的輸出數目。 您可以決定您想要包括多少個隱藏層，以及每一層中有多少神經元；但是您無法控制這些層的輸入值和輸出值，這些值都是由模型定型程序所決定。

對深度神經網路進行定型

深度神經網路的定型程序是由多個反覆運算所組成，稱為 Epoch。 針對第一個 Epoch，您首先要為權數 (w) 和偏差 b 值指派隨機的初始化值。 然後，程序如下：

  1. 系統會將具有已知標籤值之資料觀察的特徵提交至輸入層。 通常，這些觀察會分組為「批次」(通常稱為「迷你批次」)。
  2. 神經元接著會套用其函式，並會在啟用時將結果傳遞至下一層，直到輸出層產生預測為止。
  3. 預測會與實際已知值進行比較，並會計算預測值和真正值之間的變異數量 (我們稱為「損耗」)。
  4. 根據結果，會計算權數和偏差值的修訂值以減少損耗，並將這些調整「反向傳播」至網路層中的神經元。
  5. 下一個 Epoch 會使用修訂的權數和偏差值重複批次定型向前傳遞，希望透過減少損耗來改善模型的精確度。

注意

以批次方式處理定型特徵可改善定型程序的效率，方法是以權數和偏差的向量作為特徵的矩陣，同時處理多個觀察。 利用矩陣和向量運算的線性代數函式也是 3D 圖形處理中的特徵，這也是為什麼具有圖形處理器 (GPU) 的電腦，其提供給深度學習模型定型的效能明顯優於僅有中央處理器 (CPU) 的電腦。

仔細查看損耗函式和反向傳播

先前的深度學習定型程序描述，提到會計算模型中的損耗，並使用其來調整權數和偏差值。 這到底是如何運作的？

計算損耗

假設透過定型程序傳遞的其中一個範例，包含「阿德利企鵝」標本 (類別 0) 的特徵。 來自網路的正確輸出將是 [1, 0, 0]。 現在假設網路產生的輸出是 [0.4, 0.3, 0.3]。 相較這兩者，我們可以將每個元素的絕對變異數 (換句話說，每個預測值與其實際值相差多少) 計算為 [0.6, 0.3, 0.3]。

實際上，因為我們正在處理多個觀察，所以通常會彙總變異數 (例如，透過將個別變異數值平方並計算平均值)，因此最後會有單一的平均損耗值，像是 0.18。

最佳化工具

現在，這裡是聰明位元。 損耗的計算方式是使用函式，此函式會對來自網路最後一層 (其也是函式) 的結果進行運算。 網路的最後一層會對來自先前層的輸出 (其也是函式) 進行運算。 實際上，從輸入層到損耗計算的整個模型都只是一個大型巢狀函式。 這些函式具有一些非常實用的特性，包括：

  • 您可以將函式概念化為繪製的線條，以將其輸出與其每個變數進行比較。
  • 您可以使用微分，在相對於其變數的任何點計算函式的「導數」。

讓我們先來看看第一個功能。 我們可以繪製函式線條，以顯示個別權數值與損耗的比較方式，並在該線條上標記目前權數值符合目前損耗值的那一點。

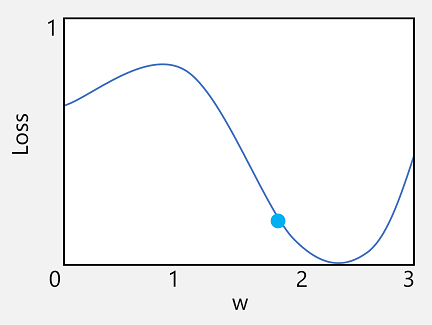
A chart showing a loss function with the current weight and loss values plotted as a point

現在讓我們套用函式的第二個特性。 給定點的函式導數指出函式輸出的斜率 (或稱「梯度」) 相對於函式變數 (在此情況下，指的是權數值) 是遞增還是遞減。 正導數指出函式正在增加，負導數則指出正在減少。 在此情況下，於目前權數值的繪製點上，函式具有向下梯度。 換句話說，增加權數會有減少損耗的效果。

我們會使用「最佳化工具」，針對模型中的所有權數和偏差變數套用這個相同的技巧，並判斷我們需要以哪個方向 (上或下) 調整這些變數，以減少模型中的整體損耗量。 有多個常用的最佳化演算法，包括「隨機梯度下降 (SGD)」、「調適型學習速率 (ADADELTA)」、「調適型動量估計 (Adam)」和其他演算法；這些演算法都是設計來了解如何調整權數和偏差，以將損耗降到最低。

學習率

現在，明顯的下一個問題是，最佳化工具應該將權數和偏差值調整多少？ 如果查看權數值的繪圖，您可以看到，小量增加權數將會向下遵循函式行 (減少損耗)，但如果我們將其增加太多，則函式行會開始再次上升，因此我們可能實際增加損耗；在下一個 Epoch 之後，我們可能會發現需要減少權數。

調整的大小是由您為定型設定的參數所控制，稱為「學習速率」。 低學習速率會導致系統進行較小型的調整 (因此可能需要更多 Eepoch 來將損耗降至最低)，而高學習速率會導致系統進行較大型的調整 (因此您可能完全遺漏最小值)。