評估分類模型

已完成

分類模型的定型精確度，比起在提供未曾見過的新資料時該模型的運作程度，較為不重要。 畢竟，我們會將模型定型，使其可用於我們在真實世界中發現的新資料。 因此，在我們將分類模型定型之後，我們會評估其如何在一組未曾見過的新資料上執行。

在先前的單元中，我們建立了一個模型，根據血糖層級來預測患者是否已經有糖尿病。 現在，當套用至部分不屬於定型集的資料時，我們會得到下列預測。

x	y	ŷ
83	0	0
119	1	1
104	1	0
105	0	1
86	0	0
109	1	1

回想一下，x 指的是血糖層級，y 指的是實際糖尿病，而 ŷ 是指模型的預測是否有糖尿病。

僅計算有多少預測是正確的，有時候可能會誤導或太過簡化，難以了解其在真實世界中的錯誤種類。 若要取得更詳細的資訊，我們可以在稱為混淆矩陣的結構中將結果表格化，如下所示：

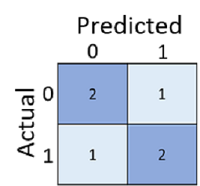
混淆矩陣會顯示下列案例的總案例數：

• 模型預測為 0，而實際標籤為 0 (確判為否，左上方)
• 模型預測為 1，而實際標籤為 1 (確判為真，右下方)
• 模型預測為 0，而實際標籤為 1 (誤判為否，左下方)
• 模型預測為 1，而實際標籤為 0 (誤判為真，右上方)

混淆矩陣中的資料格通常會加上陰影，因此越高的值具有越深的陰影。 這可讓您更輕鬆地看到從左上到右下的強式對角線趨勢，並反白顯示預測值與實際值相同的資料格。

從這些核心值計算，您可以計算可協助您評估模型效能的其他計量範圍。 例如：

• 正確性：(TP+TN)/(TP+TN+FP+FN) - 所有的預測中，有多少是正確的？
• 重新叫用：TP/(TP+FN) - 在所有確認為確定的案例中，此模型能識別出其中幾件？
• 精確度：TP/(TP+FP) - 模型預測為確定的所有案例中，實際為確定的有多少？