二元分類

  • 12 分鐘

分類就像迴歸一樣，是 受監督的 機器學習技術;因此，遵循定型、驗證和評估模型的相同反覆程序。 不同於計算類似迴歸模型的數值，用來定型分類模型的演算法會計算類別指派的 機率 值，以及用來評估模型效能的評估計量，比較預測類別與實體類別。

二元分類 演算法可用來定型模型，以預測單一類別的兩個可能標籤之一。 基本上，預測 true 或 false。 在大部分的實際案例中，用來定型和驗證模型的資料觀察包含多個特徵 (x) 值，以及 1 或 0 的 y 值。

範例 - 二元分類

若要瞭解二元分類的運作方式，讓我們看看使用單一功能 (x) 來預測標籤 y 為 1 或 0 的簡化範例。 在此範例中，我們將使用病患的血糖等級來預測病患是否具有糖尿病。 以下是我們將用來定型模型的資料:

Diagram of a syringe. Diagram of a diabetic and non-diabetic person.
血糖 (x) 糖尿病? (y)
67 0
103 1
114 1
72 0
116 1
65 0

定型二元分類模型

為了定型模型，我們將使用演算法將定型資料放入函式，以計算類別標籤為 true 的 機率 (換句話說，病患有糖尿病)。 機率的測量值介於 0.0 和 1.0 之間，因此 所有 可能類別的 總 機率都是 1.0。 因此，例如，如果患者罹患糖尿病的機率為 0.7，那麼患者為非糖尿病的對應機率為 0.3。

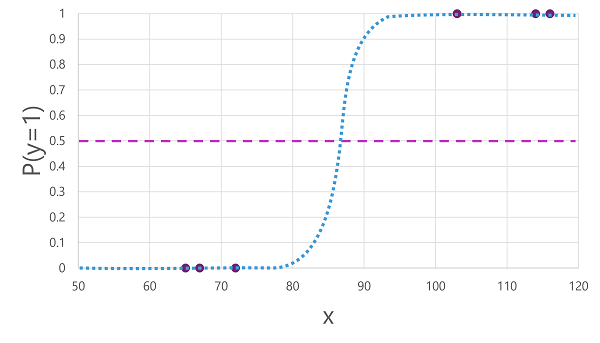
有許多演算法可用於二元分類，例如 羅吉斯迴歸，其衍生 sgmoid (S 形) 函式，其值介於 0.0 和 1.0 之間，如下所示:

Diagram of a logistic function.

注意

儘管其名稱，在機器學習中，羅吉斯迴歸 是用於分類，而不是迴歸。 重點在於它所產生的函式 羅吉斯 本質，其描述下限值和上限值之間的 S 形曲線 (用於二元分類時為 0.0 和 1.0)。

演算法所產生的函式描述 y 為 true 的機率 (y=1) 指定值為 x。 在數學上，您可以像這樣表示函式:

f(x) = P(y=1 | x)

針對定型資料中六個觀察中的三個，我們知道 y 絕對為 true，因此 y=1 為 1.0 的觀察機率，而針對其他三個觀察，我們知道 y 絕對為 false，因此y=1 的機率是 0.0。 S 形曲線描述機率分佈，讓繪製線條上的 x 值可識別 y 為 1 的對應機率。

此圖表也包含水平線，以指出根據此函式的模型預測 true (1) 或 false (0) 的 閾值。 閾值位於 y (P(y) = 0.5) 的中間點。 針對此點或以上的任何值，模型將會預測 true (1) ;而對於低於此點的任何值，則會預測為 false (0)。 例如，針對具有血糖等級為 90 的病患，此函式會產生 0.9 的機率值。 由於 0.9 高於 0.5 的閾值，因此模型會預測 true (1) - 換句話說，系統會預測病患患有糖尿病。

評估二元分類模型

如同迴歸，在定型二元分類模型時，您會保留用來驗證定型模型的隨機資料子集。 假設我們保留下列資料來驗證糖尿病分類器:

血糖 (x) 糖尿病? (y)
66 0
107 1
112 1
71 0
87 1
89 1

將我們先前衍生的羅吉斯函式套用至 x 值會產生下列繪圖。

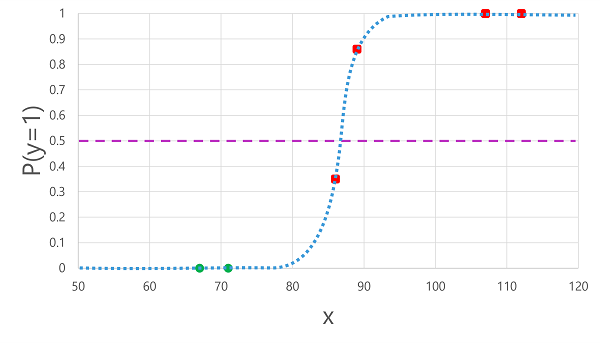
Diagram of predicted labels on a sigmoid curve.

根據函式計算的機率高於或低於閾值，模型會為每個觀察產生 1 或 0 的預測標籤。 然後，我們可以比較 預測 類別標籤 (ŷ) 與 (y) 的 實際 類別標籤，如下所示:

血糖 (x) 實際的糖尿病診斷 (y) 預測的糖尿病診斷 (ŷ)
66 0 0
107 1 1
112 1 1
71 0 0
87 1 0
89 1 1

二元分類評估計量

計算二元分類模型的評估計量的第一個步驟，通常是為每個可能類別標籤建立正確和不正確預測數目的矩陣:

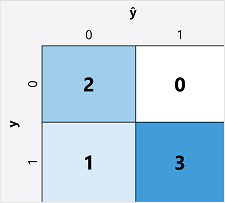
Diagram of a confusion matrix.

此視覺效果稱為 混淆矩陣，且會顯示預測總計，其中:

  • ŷ=0 和 y=0: 確判為假 (TN)
  • ŷ=1 和 y=0: 誤判為真 (FP)
  • ŷ=0 和 y=1: 誤判為假 (FN)
  • ŷ=1 和 y=1: 確判為真 (TP)

混淆矩陣的排列是正確 (true) 預測會以從左上到右下的對角線顯示。 通常，色彩強度是用來指出每個資料格中的預測數目，因此快速查看預測良好的模型應該會顯示深色對角線趨勢。

準確率

您可以從混淆矩陣計算的最簡單計量是 精確度 - 模型正確預測的比例。 精確度的計算方式如下:

(TN+TP) ÷ (TN+FN+FP+TP)

在我們的糖尿病範例中，計算為:

(2+3) ÷ (2+1+0+3)

= 5 ÷ 6

= 0.83

因此，針對我們的驗證資料，糖尿病分類模型會產生正確的預測 83%。

精確度一開始看起來可能很適合用來評估模型，但請考慮以下這點。 假設 11% 的人口患有糖尿病。 您可以建立一個一律預測為 0 的模型，而且其精確度為 89%，即使它不會實際嘗試藉由評估其特徵來區分患者。 我們真正需要的是更深入地瞭解模型如何針對正數案例預測 1，而負數案例則為 0。

重新叫用

召回率 是測量模型正確識別之正面案例比例的計量。 換句話說，與 患有 糖尿病病患的數目相比，模型 預測 有多少病患患有糖尿病?

召回率的公式如下:

TP ÷ (TP+FN)

針對我們的糖尿病範例:

3 ÷ (3+1)

= 3 ÷ 4

= 0.75

因此，我們的模型已正確識別出 75% 的糖尿病患者患有糖尿病。

精確度

精確度 與召回率類似，但會測量實際為真標籤之預測正面案例的比例。 換句話說，模型 預測 的糖尿病病患實際上 患有 糖尿病的比例是多少?

精確度的公式為:

TP ÷ (TP+FP)

針對我們的糖尿病範例:

3 ÷ (3+0)

= 3 ÷ 3

= 1.0

因此，我們模型預測的 100% 患者實際上都患有糖尿病。

F1 分數

F1 分數 是結合召回率和精確度的整體計量。 F1 分數的公式為:

(2 x 精確度 x 召回率) ÷ (精確度 + 召回率)

針對我們的糖尿病範例:

(2 x 1.0 x 0.75) ÷ (1.0 + 0.75)

= 1.5 ÷ 1.75

= 0.86

曲線下的面積 (AUC)

另一個重新叫用名稱是 確判為真 (TPR)，而有一個對等的計量名稱為 誤判為真率 (FPR)，其計算為 FP÷ (FP+TN)。 我們已知道當使用閾值為 0.5 的 TPR 為 0.75 時，我們可以使用 FPR 的公式來計算 0÷2 = 0 的值。

當然，如果我們要變更模型預測為 true(1) 的閾值，則會影響正面和負面預測的數目;因此，變更 TPR 和 FPR 計量。 這些計量通常用來評估模型，方法是繪製 接收的運算子特性 (ROC) 曲線，以比較 TPR 和 FPR 的每個可能閾值介於 0.0 到 1.0 之間:

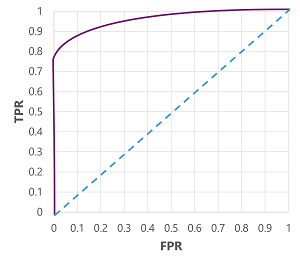
Diagram of a ROC curve.

完美模型的 ROC 曲線會沿著左邊的 TPR 軸向上，然後穿過頂部的 FPR 軸。 由於曲線的繪圖區會測量 1x1，所以這個完美曲線下的區域會是 1.0 (表示模型 100% 的時間內都正確)。 相反地，從左下到右上方的對角線代表隨機猜測二進位標籤所達成的結果;產生曲線下 0.5 的區域。 換句話說，給定兩個可能的類別標籤，您可以合理地預期在 50% 的時間內猜對。

在我們的糖尿病模型案例中，會產生上述曲線，而 曲線下的區域 (AUC) 計量為 0.875。 由於 AUC 高於 0.5，因此我們可以得出結論，該模型在預測患者是否患有糖尿病方面比隨機猜測表現更好。