什麼是量子運算中的疊加?
如果上一個單元中的貓是量子貓,量子貓和方箱系統的狀態仍為相同:量子貓相對於方箱六個不同位置的總和,而由在該位置中找到量子貓的機率予以加權。 唯一的差別在於,傳統貓可以位於六個可能位置的其中一個 (且只有一個),而量子貓可以同時處於所有六個位置!
在傳統世界中,物體一次只能處於一種狀態。 不過,在量子世界中,量子粒子可以同時處於多個狀態。 這種現象稱為疊加。
在量子運算中沒有人使用量子貓 (很遺憾),而是量子位元。 「qubit」一詞表示「量子位元」。 就像在傳統運算中一樣,其中資訊的基本單位是位元,在量子運算中,資訊的基本單位是量子位元。 就像位元可以採用兩個可能值 0 和 1 一樣,量子位元是任何可能處於兩種狀態的量子粒子。 例如,量子位元可以是光子,可兩極分化兩個方向,或電子,可以是兩個能量水準。
如何在量子位元中表示疊加? 在特定狀態下找到量子位元的機率為何?
如何在量子位元中表示疊加?
量子位元是具有兩個可能位置或「狀態」的量子粒子。 與傳統位元類似,量子位元的量子狀態也稱為 $0$ 和 $1$。 量子位元可以處於狀態 $0$、狀態 $1$,以及兩個狀態的任何疊加中。 如何表示這個疊加?
假設您繪製圓形及垂直和水平軸,使中間點是圓形的中心。 狀態 $0$ 會放在垂直軸的上層點,而狀態 $1$ 則位於下層點。
如何描述此表示法? 您可以說狀態 $0$ 是箭號,或是一種指向上方的「向量」,而狀態 $1$ 是指向下方的向量。 因此,傳統位元會是指向上方或下方的向量,但絕不會指向另一個方向。
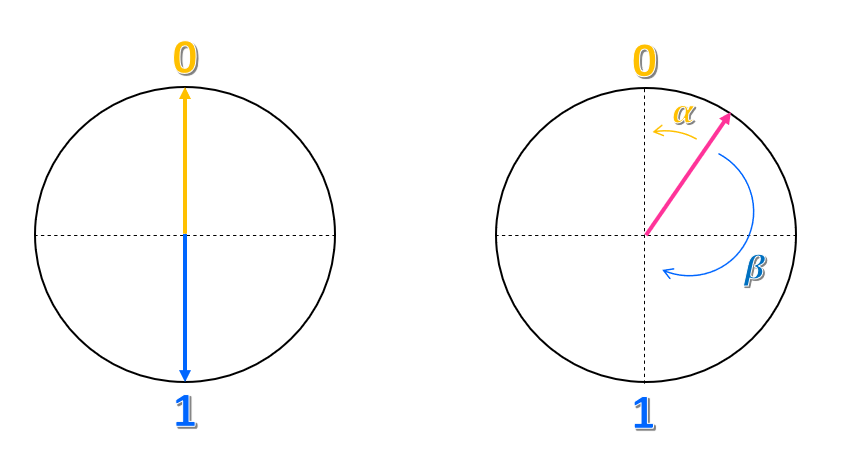
圓形的任何其他點呢? 如何表示該狀態? 就像平面中的座標一樣,您可以嘗試將其表示為兩個狀態 $0$ 和 $1$ 的組合。 例如,您可以取得向量與狀態 $0$ 的距離,然後呼叫這個角度 $\alpha$,以及距離 $1$ 狀態有多接近,並呼叫這個角度 $\beta$。 我們可以將狀態表示為 $\alpha 0 + \beta 1 $。 因此,狀態即為狀態 $0$ 和 $1$ 的「疊加」。
就像貓和方箱的範例一樣,量子位元的全域狀態是個別狀態 $0$ 和 $1$ 的總和,其加權是找出處於該狀態 $\alpha$ 和 $\beta $ 之量子位元的機率。
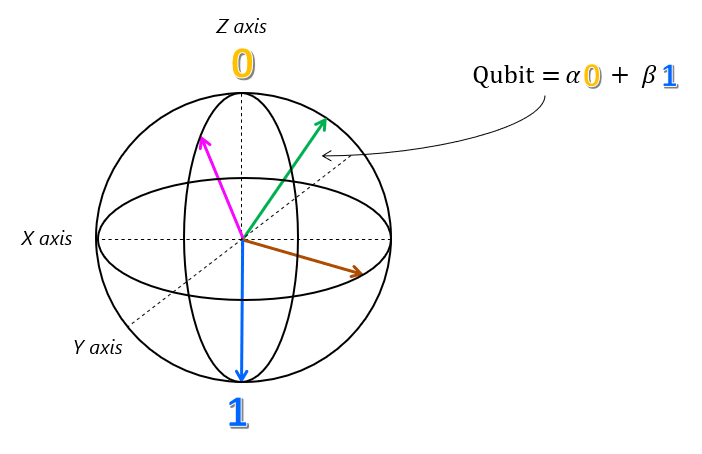
量子位元的這種表示實際上是正確的,且其稱為「布洛赫球體」。
提示
布洛赫球體是一個強大的工具,因為我們可以在量子位元上執行的作業可以表示為其中一個基軸的旋轉。 雖然將量子運算視為一連串旋轉是一種強烈的直觀,但使用此直觀來設計和描述演算法是一項挑戰。 Q# 藉由提供描述此類旋轉的語言來緩解此問題。
找到處於某種狀態之量子位元的機率為何?
就像上一個單元中的貓和方箱的範例一樣,量子位元的全域狀態是個別狀態 $0$ 和 $1$ 的總和,其加權是找出處於該狀態 $\alpha$ 和 $\beta $ 之量子位元的機率。 數字 $\alpha$ 和 $\beta$ 分別代表量子位元狀態與狀態 $0$ 和 $1$ 的「接近」程度。 那麼,$\alpha$ 和 $\beta$ 是否代表找到處於狀態 $0$ 或 $1$ 之量子位元的機率? 不完全是。
數字 $\alpha$ 和 $\beta$ 是每個狀態的「機率幅」。 其絕對值,例如 $|\alpha|^2$,提供對應的機率。 例如,觀察到狀態 $0$ 的機率是 $|\alpha|^2$,而觀察到狀態 $1$ 的機率是 $|\beta|^2$。
數字 $\alpha$ 和 $\beta$ 可以是正數、負數,甚至複數。 不過,在有效的量子疊加中,所有機率的總和必須是一:$|\alpha|^2+|\beta|^2=1$。 此條件約束稱為「正規化條件」。 您可以將正規化條件想成是您在測量時一律會取得結果的事實,因此測量每個可能結果的機率和必須是一。