如何使用纏結來傳送資訊?
在先前的單元中,您已了解量子糾纏可能是量子通訊的絕佳資源。 在此單元中,您會看到糾纏最有名的應用程式之一:量子遠端傳輸通訊協定。
在遠端傳輸中,纏結是用來將量子位元的狀態從一個位置傳輸到另一個位置。 量子位元的狀態會傳輸到另一個量子位元,但量子位元本身不會實際移動。 這是要記住的一件重要事項! 量子位元狀態的資訊會傳送至另一個量子位元,做為容器,以寫入訊息量子位元的資訊。
遠端傳輸通訊協定使用纏結和傳統通訊的組合。 傳統通訊很重要,因為傳送者需要傳送者將測量結果傳達給接收者。 這表示遠端傳輸無法使資訊的傳送比光速更快。 傳送者和接收者之間的傳統通訊受限於光線速度。
讓我們檢閱量子遠端傳送的通訊協定。
量子轉送的通訊協定
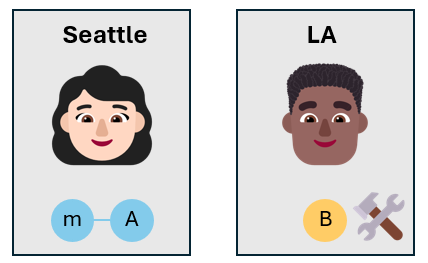
Alice 和 Bob 在同一家公司中合作。 Alice 總部設在西雅圖,Bob 位於洛杉磯。 他們正在處理需要他們共用量子資訊的專案。 他們決定使用量子遠端傳送,在它們之間傳送量子資訊。
初始設定
Alice 和 Bob 各有一個量子位元,這是先前準備的纏結配對的一部分。 纏結的配對是貝爾態,即此態
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alice 有額外的量子位元 –稱為「訊息量子位元」,而且想要將此量子位元傳送給 Bob。 訊息量子位元處於 Alice 想要傳送至 Bob 的未知狀態。 訊息量子位元的狀態為
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
其中 $\alpha$ 和 $\beta$ 是複數。
Alice 和 Bob 三個量子位元的全域狀態為
$$\ket{\text{Global}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$
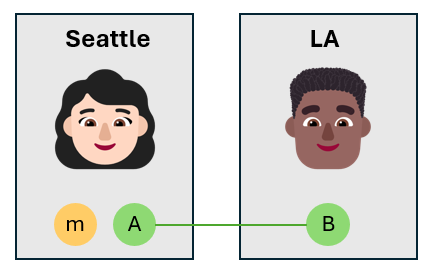
Alice 將訊息量子位元與她自己的量子位元纏結在一起
Alice 會採用訊息量子位元,並使用 CNOT 閘道將它與自己的量子位元 $A$ 纏結在一起。 訊息量子位元是控制量子位元,Alice 的量子位元是 target 量子位元。 這會建立三個量子位元纏結狀態。
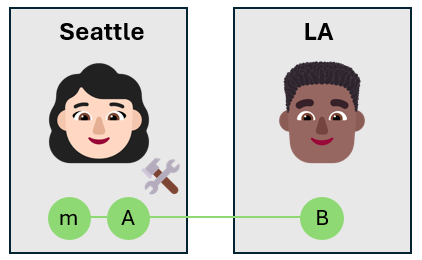
訊息量子位處於未知狀態 $\alpha\ket{0}_m + \beta\ket{1}_m$,因此套用 CNOT 閘道之後,Alice 的量子位元會處於四個貝爾態的疊加。 三個量子位元的全域狀態為
$$\ket{\text{Global}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$
$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$
$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
Alice 和 Bob 量子位元的全域狀態是四個可能狀態的疊加。
提示
確認三個量子位元的全域狀態為上述項目是個良好的練習。 您可以將 CNOT 閘道套用至訊息量子位元和 Alice 的量子位元,然後展開三個量子位元的狀態,以執行此動作。
Alice 測量量子位元
Alice 接著會測量訊息量子位元和她自己的量子位元。 她不會像往常一樣測量 $Z$中的量子位元,而是選擇貝爾基礎。 貝爾基礎包含四個貝爾狀態: $\lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, \ket{\psi^-} \rbrace$。
Alice 藉由測量訊息量子位元和她在貝爾基礎中自己的量子位元,將她的量子位元投影到四個貝爾狀態的其中一個。 由於三個量子位元會纏結,因此測量結果會相互關聯。 當 Alice 測量其量子位元時,Bob 的量子位元也會投影到相互關聯的狀態。
例如,如果 Alice 測量其量子位元並觀察狀態 $\ket{\phi^-}$,則 Bob 的量子位元會投影到狀態 $\alpha\ket{0}_B - \beta\ket{1}_B$。
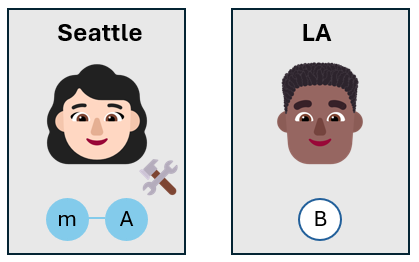
Alice 打給 Bob
Alice 打電話給 Bob,並跟他說她的測量結果。 她使用傳統通道,例如來電或簡訊。
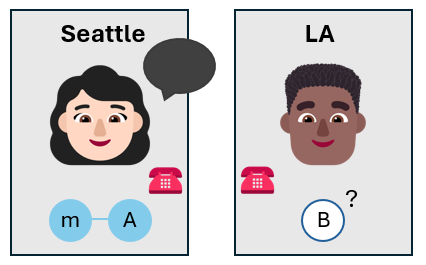
Bob 現在知道自己的量子位元狀態,而不必測量它。 Bob 量子位元的狀態可能與 Alice 想要傳送的訊息量子位元狀態不同,但它很接近。
Bob 會套用量子運算
接下來,Bob 可以將特定量子運算套用至量子位元,以復原訊息量子位元的原始狀態。 Bob 的作業取決於 Alice 透過電話告訴他的內容。
他執行的作業可以是泡利 $X$ 閘、泡利 $Z$ 閘、兩者皆是,或兩者皆非。
例如,如果 Alice 的測量結果為 $\ket{\phi^-}$,Bob 就會知道他的量子位元處於狀態 $(\alpha\ket{0}_B - \beta\ket{1}_B)$。 他只需要套用泡利 Z 閘來復原訊息量子位元的原始狀態。
| Alice 量值 | Bob 套用 |
|---|---|
| $\ket{\phi^+}$ | 無作業 |
| $\ket{\phi^-}$ | 泡利 Z 閘 |
| $\ket{\psi^+}$ | 泡利 X 閘 |
| $\ket{\psi^-}$ | 泡利 X 閘後面接著泡利 Z 閘 |
此最終作業有效地將訊息量子位元的狀態傳送到 Bob 的量子位元。 任務完成!
重要
將作業套用至量子位元與測量作業不同。 當 Bob 套用作業時,他不會測量量子位元。 他套用量子運算來變更量子位元的狀態,但不會將其折疊。