練習 - 使用 Q# 建立量子糾纏

已完成

在上一個單元中，您已了解量子糾纏和貝爾狀態的概念。

現在，讓我們使用 Q# 和 Azure Quantum Development Kit 來建立量子糾纏。 若要建立糾纏，您需要套用兩個量子運算: Hadamard 閘道和 Controlled-NOT (CNOT) 閘道。

Controlled-NOT (CNOT) 運算

當兩個量子位元糾纏時，一個量子位元的狀態相依於另一個量子位元的狀態。 因此，若要使兩個量子位元糾纏，您需要可同時作用於兩個量子位元的運算。 這稱為「多量子位元運算」。

若要建立量子糾纏，您需要多量子位元 CNOT 運算，其代表 Controlled-NOT。 此運算會採用兩個量子位元作為輸入，一個作為對照量子位元，另一個則是 target 量子位元。 CNOT 作業只會在第一個量子位元 (對照量子位元) 的狀態為 $|1\rangle$ 時，才會將第二個量子位元 (target 量子位元) 的狀態翻轉。

輸入	輸出
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

在 Q# 中，CNOT 運算會作用於兩個量子位元的陣列，如果第一個量子位元是 One，則會翻轉第二個量子位元。

使用 CNOT 運算的糾纏

套用 Hadamard、H、作業和 Controlled-NOT、CNOT、作業，您即可將狀態 $|00\rangle$ 的兩個量子位元轉換成貝爾狀態 $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$。

以下說明其運作方式：

1. 取得狀態 $|00\rangle$ 的兩個量子位元。 第一個量子位元是對照量子位元，第二個量子位元則是 target 量子位元。

2. 套用 $H$，僅只在對照量子位元中建立疊加狀態。

   $$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)$$

   提示

   下標 ${}_c$ 和 ${}_t$ 指定對照和 target 量子位元。

3. 將 $CNOT$ 運算子套用至疊加狀態的對照量子位元，以及狀態 $|0_t\rangle$ 的 target 量子位元。

   $$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t})$$

建立新的 Q# 檔案

1. 打開 Visual Studio Code。
2. 選取 [檔案] > [新增文字檔]，並將它另存為 Main.qs。
3. 選取 [檢視] -> [命令選擇區] 並鍵入 Q#：設定 Azure Quantum QIR target 設定檔。 按 Enter 鍵。
4. 選取 Q#：不受限制。

建立貝爾狀態 $\ket{\phi^+}$

讓我們從建立貝爾狀態 $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$ 開始。

1. 首先，您需要從標準連結庫匯 Microsoft.Quantum.Diagnostics 入命名空間，其中包含 DumpMachine 函式。 此函式會顯示量子位元的目前狀態。 將下列 Q# 程式碼複製並貼到 Main.qs 檔案。

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   

   提示

   您也可以藉由使用 Std 來取代 Microsoft.Quantum 以匯入標準連結庫。 例如，import Std.Diagnostics.* 相當於 import Microsoft.Quantum.Diagnostics.*。

2. 建立傳回兩個 Result 類別值的 Main 作業，也就是量子位元的測量結果。

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       // Your code goes here
   }
   

3. 在 Main 作業內，您會配置兩個量子位元 (q1 及 q2)，其將會糾纏。

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   }
   

4. 將 Hadamard 閘道 H 套用至第一個量子位元 q1，以將其置於疊加狀態。 然後，使用 CNOT 作業糾纏兩個量子位元。

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
   }
   

5. 使用 DumpMachine 函式來顯示量子位元的目前狀態。 這與測量量子位元不同。

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
   
       DumpMachine();
   }
   

6. 使用 M 作業測量量子位元，並將結果儲存在 m1 和 m2 中。 然後，使用 Reset 作業來重設量子位元。 在 Q# 中，您必須一律將量子位元重設為 $|0\rangle$ 狀態。

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
   
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
       DumpMachine();
   
       let (m1, m2) = (M(q1), M(q2));
       Reset(q1);
       Reset(q2);
   
   }
   

7. 最後，使用 return 陳述式傳回量子位元的測量結果。 您的 Main.qs 檔案看起來應該像這樣:

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       CNOT(q1, q2);
   
       DumpMachine();
   
       let (m1, m2) = (M(q1), M(q2));
       Reset(q1);
       Reset(q2);
   
       return (m1, m2);
   }
   

8. 若要在內建模擬器上執行程式，請按下 Main 作業上方的 [執行]，或按 Ctrl+F5。 您的輸出會出現在偵錯控制台中。

9. 測量結果會相互關聯，因此在程式結果，您會以相同的機率得到 (Zero, Zero) 或 (One, One) 的結果。

10. 從 Main 作業上方的命令清單中按一下 [線路]，即可將電路圖視覺化。 電路圖顯示套用至第一個量子位元的 Hadamard 邏輯閘，以及套用至這兩個量子位元的 CNOT 邏輯閘。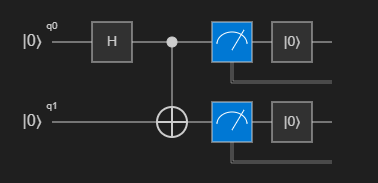

    

建立其他貝爾態

若要建立其他貝爾狀態，您必須將額外的 Pauli $X$ 和 $Z$ 運算套用至量子位元。

例如，若要建立貝爾狀態 $\ket{\phi^-}=\frac1{\sqrt2}(|00\rangle-|11\rangle)$，您可以在套用 Hadamard 邏輯閘之後，將 Pauli $Z$ 運算套用至對照量子位元。 $Z$ 運算會將狀態 $\ket{+}$ 翻轉為 $\ket{-}$。

提示

狀態 $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ 和 $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ 也分別稱為 $\ket{+}$ 和 $\ket{{-}$。

以下說明其運作方式：

1. 取得狀態 $|00\rangle$ 的兩個量子位元。

2. 套用 $H$，僅只在對照量子位元中建立疊加狀態。

   $$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+}_c$$

3. 將 $Z$ 運算套用至對照量子位元。

   $$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c\rangle-|1_c\rangle)=\ket{{-}_c$$

4. 將 $CNOT$ 運算子套用至對照量子位元和 $|0_t\rangle$ 狀態的 target 量子位元。

   $$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}-\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}-|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}-\ket{1_c 1_t})$$

同樣地，將 Pauli $X$ 和 $Z$ 運算套用至量子位元，即可建立貝爾狀態 $\ket{\psi^+}$ 和 $\ket{\psi^-}$。

• 在套用 Hadamard 邏輯閘之後，將 Pauli $X$ 運算套用至 target 量子位元，即可建立貝爾狀態 $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$。
• 在套用 Hadamard 邏輯閘之後，將 Pauli $Z$ 套用至對照量子位元並將 Pauli $X$ 套用至 target 量子位元，即可建立貝爾狀態 $\ket{\psi^-}=\frac1{\sqrt2}(|01\rangle-|10\rangle)$。

在 Q# 中建立貝爾狀態 $\ket{\phi^-}$

1. 修改 Q# 程式碼，以建立貝爾狀態 $\ket{\phi^-}$。 您的 Main.qs 檔案看起來應該像這樣:

   import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
   
   operation Main() : (Result, Result) {
       use (q1, q2) = (Qubit(), Qubit());
   
       H(q1);
       Z(q1); // Apply the Pauli Z operation to the control qubit
       CNOT(q1, q2);
   
       DumpMachine();
   
       let (m1, m2) = (M(q1), M(q2));
       Reset(q1);
       Reset(q2);
   
       return (m1, m2);
   }
   

2. 若要在內建模擬器上執行程式，請按下 Main 作業上方的 [執行]，或按 Ctrl+F5。 您的輸出會出現在偵錯控制台中。

3. 從 Main 作業上方的命令清單中按一下 [線路]，即可將電路圖視覺化。 電路圖顯示套用至第一個量子位元的 Hadamard 閘道、套用至第一個量子位的 Pauli $Z$ 閘道，以及套用至這兩個量子位元的 CNOT 閘道。

在下一個單元中，您將了解如何使用糾纏來傳送量子資訊。