聚合線條和參數化的方程式

使用 SkiaSharp 來轉譯您可以使用參數方程式定義的任何線條

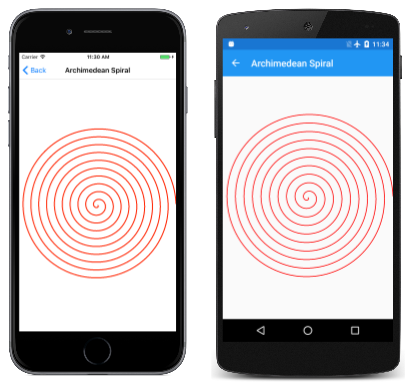
在本指南的 SkiaSharp 曲線和路徑 一節中，您會看到定義以呈現特定曲線類型的各種方法 SKPath 。 不過，有時候需要繪製一種不是直接支援的 SKPath曲線類型。 在這種情況下，您可以使用聚合線（連接線的集合）繪製任何以數學方式定義的曲線。 如果您使線條夠小且夠多，結果看起來會像曲線一樣。 這個螺旋實際上是3,600條小線：

一般而言，最好以一對參數方程式來定義曲線。 這些是相依於第三個變數的 X 和 Y 座標的方程式，有時會呼叫 t 時間。 例如，下列參數方程式會定義圓圈，其半徑為1以點 （0， 0， 0） 為 t ，從0到1：

x = cos(2πt)

y = sin(2πt)

如果您想要大於 1 的半徑，只要將正弦值和餘弦值乘以該半徑，而且如果您需要將中心移到另一個位置，請新增這些值：

x = xCenter + radius·cos(2πt)

y = yCenter + radius·sin(2πt)

對於與水準和垂直平行座標軸的橢圓形，涉及兩個弧度：

x = xCenter + xRadius·cos(2πt)

y = yCenter + yRadius·sin(2πt)

然後，您可以將對等的SkiaSharp程式代碼放入迴圈中，以計算各種點，並將這些點新增至路徑。 下列 SkiaSharp 程式代碼會 SKPath 為填滿顯示表面的橢圓形建立 物件。 迴圈會直接迴圈 360 度。 中央是顯示表面的一半寬度和高度，因此是兩個弧度：

SKPath path = new SKPath();

for (float angle = 0; angle < 360; angle += 1)
{
    double radians = Math.PI * angle / 180;
    float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
    float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);

    if (angle == 0)
    {
        path.MoveTo(x, y);
    }
    else
    {
        path.LineTo(x, y);
    }
}
path.Close();

這會產生由360小行定義的橢圓形。 轉譯時，看起來會很順利。

當然，您不需要使用聚合線建立橢圓形，因為 SKPath 包含 AddOval 為您執行橢圓形的方法。 但是，您可能想要繪製不是 由 提供的 SKPath視覺物件。

Archimedean 螺旋 頁面的程式代碼與橢圓形程式代碼類似，但有重要差異。 它會繞著圓形 360 度迴圈 10 次，持續調整半徑：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float radius = Math.Min(center.X, center.Y);

    using (SKPath path = new SKPath())
    {
        for (float angle = 0; angle < 3600; angle += 1)
        {
            float scaledRadius = radius * angle / 3600;
            double radians = Math.PI * angle / 180;
            float x = center.X + scaledRadius * (float)Math.Cos(radians);
            float y = center.Y + scaledRadius * (float)Math.Sin(radians);
            SKPoint point = new SKPoint(x, y);

            if (angle == 0)
            {
                path.MoveTo(point);
            }
            else
            {
                path.LineTo(point);
            }
        }

        SKPaint paint = new SKPaint
        {
            Style = SKPaintStyle.Stroke,
            Color = SKColors.Red,
            StrokeWidth = 5
        };

        canvas.DrawPath(path, paint);
    }
}

結果也稱為 算術螺旋， 因為每個迴圈之間的位移是常數：

請注意， SKPath 會在區塊中 using 建立 。 這會 SKPath 耗用比 SKPath 先前程式中的物件更多的記憶體，這表示 using 區塊更適合用來處置任何 Unmanaged 資源。

相關連結

• SkiaSharp API