三種類型的貝茲曲線

發行項
05/25/2017

探索如何使用 SkiaSharp 來轉譯立方體、二次方和圓錐貝塞爾曲線

貝塞爾曲線以皮埃爾·貝塞爾（1910-1999年）命名，他是雷諾汽車公司法國工程師，他利用曲線設計汽車主體。

貝塞爾曲線以適合互動式設計而聞名：它們表現良好，換句話說，沒有單數導致曲線變得無限或不笨拙的奇數，而且通常很美觀：

範例貝塞爾曲線

計算機型字型的字元外框通常以貝塞爾曲線定義。

貝塞爾曲線上的維琪百科文章包含一些有用的背景資訊。貝塞爾曲線一詞實際上是指類似曲線的家族。 SkiaSharp 支援三種類型的貝塞爾曲線，稱為立方體、二次方和圓錐。 圓錐體也稱為 理性二次方。

立方貝塞爾曲線

立方體是貝氏曲線的類型，大多數開發人員在貝氏曲線的主題出現時會想到。

您可以使用方法搭配三個SKPath參數，或使用CubicTo具有個別SKPointx和y參數的多載，將立方體 Bézier 曲線新增至物件CubicTo：

public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)

public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)

曲線從輪廓的目前點開始。完整的立方貝氏曲線是由四點所定義：

起點：目前在輪廓中的點，如果 MoveTo 尚未呼叫，則為（0， 0）
第一個控制點： point1 在 CubicTo 呼叫中
第二個控制點： point2 在 CubicTo 呼叫中
端點：point3在呼叫中CubicTo

結果曲線從起點開始，結束於終點。曲線通常不會通過兩個控制點：相反，控制點的功能非常像磁石，以將曲線拉向它們。

獲得立方貝塞爾曲線感覺的最佳方式是實驗。這是 Bezier Curve 頁面的用途，其衍生自 InteractivePage。 BezierCurvePage.xaml 檔案會具現化 SKCanvasView 和。TouchEffect 程序 代碼後置檔案BezierCurvePage.xaml.cs 在其建構函式中建立四 TouchPoint 個物件。 PaintSurface事件處理程式會SKPath建立，以根據四TouchPoint個對象呈現 Bézier 曲線，同時從控制點繪製點到終點的虛線線：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Draw path with cubic Bezier curve
    using (SKPath path = new SKPath())
    {
        path.MoveTo(touchPoints[0].Center);
        path.CubicTo(touchPoints[1].Center,
                     touchPoints[2].Center,
                     touchPoints[3].Center);

        canvas.DrawPath(path, strokePaint);
    }

    // Draw tangent lines
    canvas.DrawLine(touchPoints[0].Center.X,
                    touchPoints[0].Center.Y,
                    touchPoints[1].Center.X,
                    touchPoints[1].Center.Y, dottedStrokePaint);

    canvas.DrawLine(touchPoints[2].Center.X,
                    touchPoints[2].Center.Y,
                    touchPoints[3].Center.X,
                    touchPoints[3].Center.Y, dottedStrokePaint);

    foreach (TouchPoint touchPoint in touchPoints)
    {
       touchPoint.Paint(canvas);
    }
}

這裡正在執行：

從數學上看，曲線是立方多項式。曲線最多會在三點處交集直線。在起點處，曲線一律是正切的，而且方向與從起點到第一個控制點的直線相同。在終點，曲線一律是正切的，而且方向與從第二個控制點到終點的直線相同。

三次方貝塞爾曲線一律由連接四點的凸四邊線所限定。這稱為凸殼。如果控制點位於起點和終點之間的直線上，則貝塞爾曲線會轉譯為直線。但曲線也可以交叉本身，如第三個螢幕快照所示。

路徑輪廓可以包含多個連接的立方貝塞爾曲線，但兩個立方貝塞爾曲線之間的連接只有在下列三點是粗線（也就是躺在直線上）才會平滑：

第一個曲線的第二個控制點
第一個曲線的終點，這也是第二個曲線的起點
第二個曲線的第一個控制點

在下一篇關於 SVG 路徑數據的文章中，您將探索一個工具，以簡化平滑連接貝塞爾曲線的定義。

有時候，了解呈現立方貝塞爾曲線的基礎參數方程式會很有用。對於 從 0 到 1 的 t 範圍，參數方程式如下所示：

x（t） = （1 – t）ーx₀ + 3t（1 – t）ーx₁ + 3tー（1 – t）xー + tーx₃

y（t） = （1 – t）ーy₀ + 3t（1 – t）ーy₁ + 3tー（1 – t）yー + tーy₃

3 的最高指數證實，這些是立方多項式。很容易確認當等於 0 時 t ，點是（x₀， y₀），這是起點，而當 t 等於 1 時，點是（x₃， y₃），這是結束點。接近起點（針對的低值 t），第一個控制點（x₁，y₁）有很強的效果，而接近終點（高值 't'）的第二個控制點（xー， yー）有很強的效果。

貝塞爾曲線近似圓弧

使用貝塞爾曲線轉譯圓弧有時很方便。立方貝塞爾曲線可以近似圓弧非常接近四分之一圓形，因此四個連接的貝塞爾曲線可以定義整個圓形。此近似值會在 25 年前發表的兩篇文章中討論：

Tor Dokken等人，“彎曲-連續貝塞爾曲線的圓形良好近似值” ，計算機輔助幾何設計7 （1990年），33-41。

Michael Goldapp，“由立方多項式的圓弧近似”， 計算機輔助幾何設計8 （1991年），227-238。

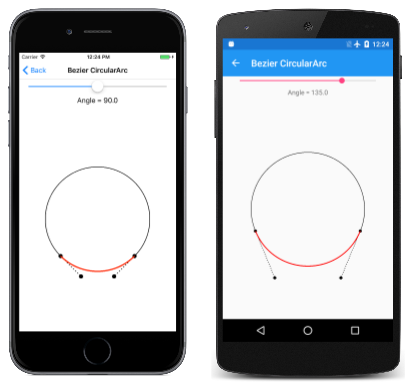
下圖顯示標示 pto為、 pt1、 pt2和的四個點，並 pt3 定義近似圓弧的 Bézier 曲線（以紅色顯示）：

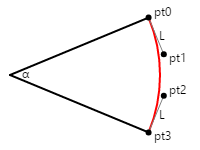
圓弧與貝氏曲線的近似值

從起點和終點到控制點的線條會與圓形和貝塞爾曲線相切，而且其長度為 L。上述第一篇文章指出，貝塞爾曲線最好在計算出這樣的長度 L 時，最接近圓弧：

L = 4 × tan（α / 4） / 3

此圖顯示 45 度的角度，因此 L 等於 0.265。在程式代碼中，該值會乘以圓形的所需半徑。

Bezier 圓形弧線頁面可讓您實驗如何定義貝塞爾曲線，以近似圓弧，以取得高達 180 度的角度。 BezierCircularArcPage.xaml 檔案會具現化和 SliderSKCanvasView ，以便選取角度。 PaintSurfaceBezierCircularArgPage.xaml.cs程式代碼後置檔案中的事件處理程式會使用轉換，將點（0， 0）設定為畫布中央。它會繪製以該點為中心進行比較的圓形，然後計算貝塞爾曲線的兩個控制點：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Translate to center
    canvas.Translate(info.Width / 2, info.Height / 2);

    // Draw the circle
    float radius = Math.Min(info.Width, info.Height) / 3;
    canvas.DrawCircle(0, 0, radius, blackStroke);

    // Get the value of the Slider
    float angle = (float)angleSlider.Value;

    // Calculate length of control point line
    float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;

    // Calculate sin and cosine for half that angle
    float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
    float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);

    // Find the end points
    SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
    SKPoint point3 = new SKPoint(radius * sin, radius * cos);

    // Find the control points
    SKPoint point0Normalized = Normalize(point0);
    SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
                                          -length * point0Normalized.X);

    SKPoint point3Normalized = Normalize(point3);
    SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
                                          length * point3Normalized.X);

    // Draw the points
    canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
    canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
    canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
    canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);

    // Draw the tangent lines
    canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
    canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);

    // Draw the Bezier curve
    using (SKPath path = new SKPath())
    {
        path.MoveTo(point0);
        path.CubicTo(point1, point2, point3);
        canvas.DrawPath(path, redStroke);
    }
}

// Vector methods
SKPoint Normalize(SKPoint v)
{
    float magnitude = Magnitude(v);
    return new SKPoint(v.X / magnitude, v.Y / magnitude);
}

float Magnitude(SKPoint v)
{
    return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}

起點和終點（point0 和 point3）是根據圓形的一般參數方程序來計算。由於圓形是以（0， 0）置中，因此這些點也可以視為從圓形中心到圓周的星形向量。控制點位於與圓形正切的線條上，因此它們位於這些星形向量的右角度。向量從右角度到另一個向量只是交換 X 和 Y 座標的原始向量，其中一個會成為負數。

以下是以不同角度執行的程式：

仔細查看第三個螢幕快照，您會看到當角度為180度時，Bézier 曲線明顯偏離半圓形，但iOS畫面顯示，當角度為90度時，它似乎適合四分之一圓。

計算兩個控制點的座標相當容易，四分之一圓形會像這樣：

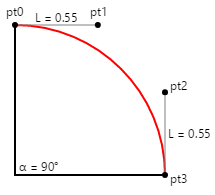
四分之一圓形與貝塞爾曲線的近似值

如果圓形的半徑為 100，則 L 為 55，這是容易記住的數位。

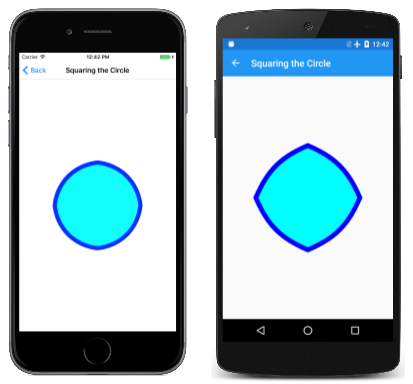
[ 四分圓 ] 頁面會以動畫顯示圓形與正方形之間的圖形。圓形大約是四個貝氏曲線，其座標會顯示在類別中這個陣列定義 SquaringTheCirclePage 的第一個資料行：

public class SquaringTheCirclePage : ContentPage
{
    SKPoint[,] points =
    {
        { new SKPoint(   0,  100), new SKPoint(     0,    125), new SKPoint() },
        { new SKPoint(  55,  100), new SKPoint( 62.5f,  62.5f), new SKPoint() },
        { new SKPoint( 100,   55), new SKPoint( 62.5f,  62.5f), new SKPoint() },
        { new SKPoint( 100,    0), new SKPoint(   125,      0), new SKPoint() },
        { new SKPoint( 100,  -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
        { new SKPoint(  55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
        { new SKPoint(   0, -100), new SKPoint(     0,   -125), new SKPoint() },
        { new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
        { new SKPoint(-100,  -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
        { new SKPoint(-100,    0), new SKPoint(  -125,      0), new SKPoint() },
        { new SKPoint(-100,   55), new SKPoint(-62.5f,  62.5f), new SKPoint() },
        { new SKPoint( -55,  100), new SKPoint(-62.5f,  62.5f), new SKPoint() },
        { new SKPoint(   0,  100), new SKPoint(     0,    125), new SKPoint() }
    };
    ...
}

第二個數據行包含四個貝塞爾曲線的座標，其區域與圓形的區域大致相同。（繪製一個方塊與 指定圓的確切 區域是經典無法解決的幾何問題，將圓形四合一。若要轉譯具有貝塞爾曲線的正方形，每個曲線的兩個控制點都相同，而且它們與起點和終點相粗，因此貝塞爾曲線會轉譯為直線。

陣列的第三個數據行是針對動畫的插補值。頁面會設定 16 毫秒的定時器，並以 PaintSurface 該速率呼叫處理程式：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    canvas.Translate(info.Width / 2, info.Height / 2);
    canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));

    // Interpolate
    TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
    float t = (float)(timeSpan.TotalSeconds % 3 / 3);   // 0 to 1 every 3 seconds
    t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2;     // 0 to 1 to 0 sinusoidally

    for (int i = 0; i < 13; i++)
    {
        points[i, 2] = new SKPoint(
            (1 - t) * points[i, 0].X + t * points[i, 1].X,
            (1 - t) * points[i, 0].Y + t * points[i, 1].Y);
    }

    // Create the path and draw it
    using (SKPath path = new SKPath())
    {
        path.MoveTo(points[0, 2]);

        for (int i = 1; i < 13; i += 3)
        {
            path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
        }
        path.Close();

        canvas.DrawPath(path, cyanFill);
        canvas.DrawPath(path, blueStroke);
    }
}

這些點會根據的正弦振蕩值 t進行插補。然後，插補點會用來建構一系列四條連接的貝塞爾曲線。以下是正在執行的動畫：

如果沒有演算法彈性足以轉譯為圓弧和直線的曲線，這類動畫就不可能實現。

貝塞爾無限頁面也利用貝塞爾曲線近似圓弧的能力。以下是類別中的PaintSurfaceBezierInfinityPage處理程式：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.MoveTo(0, 0);                                // Center
        path.CubicTo(  50,  -50,   95, -100,  150, -100); // To top of right loop
        path.CubicTo( 205, -100,  250,  -55,  250,    0); // To far right of right loop
        path.CubicTo( 250,   55,  205,  100,  150,  100); // To bottom of right loop
        path.CubicTo(  95,  100,   50,   50,    0,    0); // Back to center  
        path.CubicTo( -50,  -50,  -95, -100, -150, -100); // To top of left loop
        path.CubicTo(-205, -100, -250,  -55, -250,    0); // To far left of left loop
        path.CubicTo(-250,   55, -205,  100, -150,  100); // To bottom of left loop
        path.CubicTo( -95,  100,  -50,   50,    0,    0); // Back to center
        path.Close();

        SKRect pathBounds = path.Bounds;
        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
                                     info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

在圖表紙上繪製這些座標可能是一個很好的練習，以查看它們如何相關。無限號以點（0， 0）為中心，而兩個迴圈的中心為（–150， 0）和（150， 0）和 100 的弧度。在一 CubicTo 系列命令中，您可以看到控制點的 X 座標接受 –95 和 –205 的值（這些值為 –150 加減 55）、205 和 95 （150 加減 55），以及右邊和左側的 250 和 –250。唯一的例外狀況是當無限號在中央交叉時。在此情況下，控制點具有 50 和 –50 的組合座標，以在中心附近理順曲線。

以下是無限號：

它比從 [三種方式繪製 Arc] 文章中，Arc Infinity 頁面所呈現的無限符號更平滑。

二次方貝塞爾曲線

二次方貝塞爾曲線只有一個控制點，而曲線只由三個點定義：起點、控制點和終點。參數方程式與立方貝塞爾曲線非常類似，不同之處在於最高指數為 2，因此曲線為二次方數：

x（t） = （1 – t）ーx₀ + 2t（1 – t）x₁ + tーxー

y（t） = （1 – t）ーy₀ + 2t（1 – t）y₁ + tーyー

若要將二次方貝塞爾曲線新增至路徑，請使用 QuadTo 方法或 QuadTo 多載搭配個別 x 和 y 座標：

public void QuadTo (SKPoint point1, SKPoint point2)

public void QuadTo (Single x1, Single y1, Single x2, Single y2)

方法會將目前位置的曲線新增至 point2 ，做 point1 為控制點。

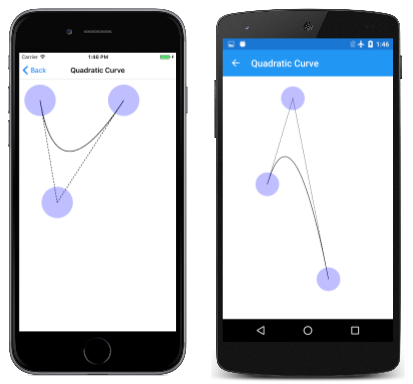
您可以使用二次方曲線頁面來實驗二次方貝塞爾曲線，這與貝塞爾曲線頁面非常類似，但只有三個接觸點。以下是PaintSurfaceQuadraticCurve.xaml.cs程序代碼後置檔案中的處理程式：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Draw path with quadratic Bezier
    using (SKPath path = new SKPath())
    {
        path.MoveTo(touchPoints[0].Center);
        path.QuadTo(touchPoints[1].Center,
                    touchPoints[2].Center);

        canvas.DrawPath(path, strokePaint);
    }

    // Draw tangent lines
    canvas.DrawLine(touchPoints[0].Center.X,
                    touchPoints[0].Center.Y,
                    touchPoints[1].Center.X,
                    touchPoints[1].Center.Y, dottedStrokePaint);

    canvas.DrawLine(touchPoints[1].Center.X,
                    touchPoints[1].Center.Y,
                    touchPoints[2].Center.X,
                    touchPoints[2].Center.Y, dottedStrokePaint);

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

在這裡，它正在執行：

虛線是起點和終點曲線的正切線，並符合控制點。

如果您需要一般形狀的曲線，二次方貝塞爾是不錯的，但您偏好只使用一個控制點而不是兩個控制點的便利性。二次方貝塞爾會比任何其他曲線更有效率地轉譯，這就是為什麼它在Skia內部用來呈現橢圓形弧線的原因。

不過，二次方貝塞爾曲線的形狀不是橢圓形，這就是為什麼需要多個二次方貝塞爾來近似橢圓弧線的原因。二次方貝塞爾是一個跳線的片段。

圓錐貝塞爾曲線

圓錐貝塞爾曲線——也稱為理性二次方貝塞爾曲線——是比塞爾曲線家族的一個相對較近的補充。和二次方貝塞爾曲線一樣，理性的二次方貝塞爾曲線牽涉到起點、終點和一個控制點。但理性的二次方貝塞爾曲線也需要加權值。它被稱為理性二次方，因為參數公式涉及比率。

X 和 Y 的參數方程式是共用相同分母的比例。以下是 t 從 0 到 1 的分母方程式，以及 w 的加權值：

d（t） = （1 – t）2wt（1 – t） + t{t

理論上，理性的二次方值可以涉及三個不同的權數值，三個詞彙各一個，但這些值可以簡化為中間的一個權數值。

X 和 Y 座標的參數方程式與二次方程式貝塞爾的參數方程序類似，不同之處在於中間詞彙也包含權數值，而表達式會除以分母：

x（t） = （1 – t）ーx₀ + 2wt（1 – t）x₁ + tーxー）） ÷ d（t）

y（t） = （（1 – t）ーy₀ + 2wt（1 – t）y₁ + tーyー）） ÷ d（t）

理性二次方貝塞爾曲線也稱為 圓錐體，因為它們可以確切地代表任何圓 錐區段的區段-雙曲、雙曲線、橢圓形和圓形。

若要將理性二次方貝塞爾曲線新增至路徑，請使用 ConicTo 方法或 ConicTo 多載搭配個別 x 和 y 座標：

public void ConicTo (SKPoint point1, SKPoint point2, Single weight)

public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)

請注意最後一個 weight 參數。

[ 圓錐曲線 ] 頁面可讓您實驗這些曲線。 ConicCurvePage 類別衍生自 InteractivePage。 ConicCurvePage.xaml 檔案會具現化，Slider以選取介於 –2 和 2 之間的權數值。 程式 代碼後置檔案ConicCurvePage.xaml.cs 會建立三個 TouchPoint 物件，而 PaintSurface 處理程式只會使用正切線將結果曲線呈現至控制點：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Draw path with conic curve
    using (SKPath path = new SKPath())
    {
        path.MoveTo(touchPoints[0].Center);
        path.ConicTo(touchPoints[1].Center,
                     touchPoints[2].Center,
                     (float)weightSlider.Value);

        canvas.DrawPath(path, strokePaint);
    }

    // Draw tangent lines
    canvas.DrawLine(touchPoints[0].Center.X,
                    touchPoints[0].Center.Y,
                    touchPoints[1].Center.X,
                    touchPoints[1].Center.Y, dottedStrokePaint);

    canvas.DrawLine(touchPoints[1].Center.X,
                    touchPoints[1].Center.Y,
                    touchPoints[2].Center.X,
                    touchPoints[2].Center.Y, dottedStrokePaint);

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

這裡正在執行：

如您所見，當權數較高時，控制點似乎會更向它拉曲線。當權數為零時，曲線會變成從起點到終點的直線。

理論上，允許負權數，並導致曲線偏離控制點。不過，–1 或以下的權數會導致參數方程式中的分母對 t 的特定值變成負數。可能基於這個原因，方法中 ConicTo 會忽略負加權。 Conic Curve 程式可讓您設定負加權，但如實驗所見，負權數的效果與零的加權相同，並導致直線呈現。

很容易衍生控制點和權數，以使用 ConicTo 方法來繪製圓弧向上（但不包括）半圓形。在下圖中，起點和終點的正切線會符合控制點。

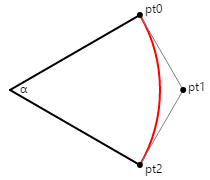
圓弧轉譯圓錐形弧線

您可以使用三角測量來判斷控制點與圓形中心距離：它是圓圈的半徑除以角度α的餘弦值。若要在起點和終點之間繪製圓弧，請將權數設定為半角的相同餘弦值。請注意，如果角度為 180 度，則正切線永遠不會符合且權數為零。但是，對於不到180度的角度，數學效果很好。

[ 圓錐形弧線 ] 頁面會示範這一點。 ConicCircularArc.xaml 檔案會具現化 Slider 來選取角度。 PaintSurfaceConicCircularArc.xaml.cs程式代碼後置檔案中的處理程式會計算控制點和權數：

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Translate to center
    canvas.Translate(info.Width / 2, info.Height / 2);

    // Draw the circle
    float radius = Math.Min(info.Width, info.Height) / 4;
    canvas.DrawCircle(0, 0, radius, blackStroke);

    // Get the value of the Slider
    float angle = (float)angleSlider.Value;

    // Calculate sin and cosine for half that angle
    float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
    float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);

    // Find the points and weight
    SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
    SKPoint point1 = new SKPoint(0, radius / cos);
    SKPoint point2 = new SKPoint(radius * sin, radius * cos);
    float weight = cos;

    // Draw the points
    canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
    canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
    canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);

    // Draw the tangent lines
    canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
    canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);

    // Draw the conic
    using (SKPath path = new SKPath())
    {
        path.MoveTo(point0);
        path.ConicTo(point1, point2, weight);
        canvas.DrawPath(path, redStroke);
    }
}

如您所見，紅色顯示的路徑與基礎圓形之間 ConicTo 沒有視覺差異，以供參考：

但將角度設定為180度，數學失敗。

在此案例中， ConicTo 它並不支援負權數，因為理論上（根據參數方程式），圓圈可以使用相同點的另一個呼叫 ConicTo 來完成，但加權的負值。這將允許根據任何角度（但不包括）零度和180度之間的任何角度，建立一個只有兩 ConicTo 個曲線的整個圓形。

SkiaSharp API

共用方式為

三種類型的貝茲曲線

立方貝塞爾曲線

貝塞爾曲線近似圓弧

二次方貝塞爾曲線

圓錐貝塞爾曲線

其他資源

共用方式為

三種類型的貝茲曲線

立方貝塞爾曲線

貝塞爾曲線近似圓弧

二次方貝塞爾曲線

圓錐貝塞爾曲線

相關連結

其他資源