執行資源估算器的不同方式

發行項
05/25/2024

在本文中，您將瞭解如何使用 Azure Quantum Resource Estimator。資源估算器是 Quantum 開發工具包的一部分，可在不同的平臺和 IDE 中使用。

如果您執行 Q# 程式，可以使用 Quantum Development Kit 擴充功能在 Visual Studio Code 中使用資源估算器。您不需要有 Azure 訂用帳戶，即可在 Visual Studio Code 中使用資源估算器。

如果您執行 Qiskit 或 QIR 程式，資源估算器可在 Azure 入口網站中使用，而且您需要 Azure 訂用帳戶才能使用它。

下表顯示執行資源估算器的不同方式。

使用者案例	平台	教學課程
估計 Q# 計劃的資源	Visual Studio Code	在頁面頂端的 VS Code 中選取 Q#
估計 Q# 計劃的資源（進階）	Visual Studio Code 中的 Jupyter Notebook	在頁面頂端的 Jupyter Notebook 中選取 Q#
估計 Qiskit 計劃的資源	Azure 入口網站	選取頁面頂端 Azure 入口網站的 Qiskit
估計 QIR 計劃的資源	Azure 入口網站	提交 QIR
使用 FCIDUMP 檔案作為自變數參數（進階）	Visual Studio Code	提交量子化學問題

VS Code 的必要條件

最新版的 Visual Studio Code 或開啟 Web上的 VS Code。
最新版的 Azure Quantum 開發套件延伸模組。如需安裝詳細數據，請參閱在 VS Code 上安裝 QDK。

提示

您不需要有 Azure 帳戶來執行本機資源估算器。

建立新的 Q# 檔案

開啟 Visual Studio Code，然後選取 [檔案 > 新增文字檔] 以建立新的檔案。
將檔案儲存為 ShorRE.qs。此檔案會包含您程式的 Q# 程式碼。

建立量子演算法

將下列程式代碼複製到 ShorRE.qs 檔案中：


    import Std.Arrays.*;
    import Std.Canon.*;
    import Std.Convert.*;
    import Std.Diagnostics.*;
    import Std.Math.*;
    import Std.Measurement.*;
    import Microsoft.Quantum.Unstable.Arithmetic.*;
    import Std.ResourceEstimation.*;

    operation Main() : Unit {
        let bitsize = 31;

        // When choosing parameters for `EstimateFrequency`, make sure that
        // generator and modules are not co-prime
        let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
    }

    // In this sample we concentrate on costing the `EstimateFrequency`
    // operation, which is the core quantum operation in Shors algorithm, and
    // we omit the classical pre- and post-processing.

    /// # Summary
    /// Estimates the frequency of a generator
    /// in the residue ring Z mod `modulus`.
    ///
    /// # Input
    /// ## generator
    /// The unsigned integer multiplicative order (period)
    /// of which is being estimated. Must be co-prime to `modulus`.
    /// ## modulus
    /// The modulus which defines the residue ring Z mod `modulus`
    /// in which the multiplicative order of `generator` is being estimated.
    /// ## bitsize
    /// Number of bits needed to represent the modulus.
    ///
    /// # Output
    /// The numerator k of dyadic fraction k/2^bitsPrecision
    /// approximating s/r.
    operation EstimateFrequency(
        generator : Int,
        modulus : Int,
        bitsize : Int
    )
    : Int {
        mutable frequencyEstimate = 0;
        let bitsPrecision =  2 * bitsize + 1;

        // Allocate qubits for the superposition of eigenstates of
        // the oracle that is used in period finding.
        use eigenstateRegister = Qubit[bitsize];

        // Initialize eigenstateRegister to 1, which is a superposition of
        // the eigenstates we are estimating the phases of.
        // We first interpret the register as encoding an unsigned integer
        // in little endian encoding.
        ApplyXorInPlace(1, eigenstateRegister);
        let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);

        // Use phase estimation with a semiclassical Fourier transform to
        // estimate the frequency.
        use c = Qubit();
        for idx in bitsPrecision - 1..-1..0 {
            within {
                H(c);
            } apply {
                // `BeginEstimateCaching` and `EndEstimateCaching` are the operations
                // exposed by Azure Quantum Resource Estimator. These will instruct
                // resource counting such that the if-block will be executed
                // only once, its resources will be cached, and appended in
                // every other iteration.
                if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
                    Controlled oracle([c], (1 <<< idx, eigenstateRegister));
                    EndEstimateCaching();
                }
                R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
            }
            if MResetZ(c) == One {
                set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
            }
        }

        // Return all the qubits used for oracles eigenstate back to 0 state
        // using Microsoft.Quantum.Intrinsic.ResetAll.
        ResetAll(eigenstateRegister);

        return frequencyEstimate;
    }

    /// # Summary
    /// Interprets `target` as encoding unsigned little-endian integer k
    /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
    /// p is `power`, g is `generator` and N is `modulus`.
    ///
    /// # Input
    /// ## generator
    /// The unsigned integer multiplicative order ( period )
    /// of which is being estimated. Must be co-prime to `modulus`.
    /// ## modulus
    /// The modulus which defines the residue ring Z mod `modulus`
    /// in which the multiplicative order of `generator` is being estimated.
    /// ## power
    /// Power of `generator` by which `target` is multiplied.
    /// ## target
    /// Register interpreted as little endian encoded which is multiplied by
    /// given power of the generator. The multiplication is performed modulo
    /// `modulus`.
    internal operation ApplyOrderFindingOracle(
        generator : Int, modulus : Int, power : Int, target : Qubit[]
    )
    : Unit
    is Adj + Ctl {
        // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
        // also use `ExpModI` to compute a by which x must be multiplied. Also
        // note that we interpret target as unsigned integer in little-endian
        // encoding.
        ModularMultiplyByConstant(modulus,
                                    ExpModI(generator, power, modulus),
                                    target);
    }

    /// # Summary
    /// Performs modular in-place multiplication by a classical constant.
    ///
    /// # Description
    /// Given the classical constants `c` and `modulus`, and an input
    /// quantum register  |𝑦⟩, this operation
    /// computes `(c*x) % modulus` into |𝑦⟩.
    ///
    /// # Input
    /// ## modulus
    /// Modulus to use for modular multiplication
    /// ## c
    /// Constant by which to multiply |𝑦⟩
    /// ## y
    /// Quantum register of target
    internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
    : Unit is Adj + Ctl {
        use qs = Qubit[Length(y)];
        for (idx, yq) in Enumerated(y) {
            let shiftedC = (c <<< idx) % modulus;
            Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
        }
        ApplyToEachCA(SWAP, Zipped(y, qs));
        let invC = InverseModI(c, modulus);
        for (idx, yq) in Enumerated(y) {
            let shiftedC = (invC <<< idx) % modulus;
            Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
        }
    }

    /// # Summary
    /// Performs modular in-place addition of a classical constant into a
    /// quantum register.
    ///
    /// # Description
    /// Given the classical constants `c` and `modulus`, and an input
    /// quantum register  |𝑦⟩, this operation
    /// computes `(x+c) % modulus` into |𝑦⟩.
    ///
    /// # Input
    /// ## modulus
    /// Modulus to use for modular addition
    /// ## c
    /// Constant to add to |𝑦⟩
    /// ## y
    /// Quantum register of target
    internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
    : Unit is Adj + Ctl {
        body (...) {
            Controlled ModularAddConstant([], (modulus, c, y));
        }
        controlled (ctrls, ...) {
            // We apply a custom strategy to control this operation instead of
            // letting the compiler create the controlled variant for us in which
            // the `Controlled` functor would be distributed over each operation
            // in the body.
            //
            // Here we can use some scratch memory to save ensure that at most one
            // control qubit is used for costly operations such as `AddConstant`
            // and `CompareGreaterThenOrEqualConstant`.
            if Length(ctrls) >= 2 {
                use control = Qubit();
                within {
                    Controlled X(ctrls, control);
                } apply {
                    Controlled ModularAddConstant([control], (modulus, c, y));
                }
            } else {
                use carry = Qubit();
                Controlled AddConstant(ctrls, (c, y + [carry]));
                Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
                Controlled AddConstant([carry], (modulus, y));
                Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
            }
        }
    }

    /// # Summary
    /// Performs in-place addition of a constant into a quantum register.
    ///
    /// # Description
    /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
    /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
    ///
    /// # Input
    /// ## c
    /// Constant number to add to |𝑦⟩.
    /// ## y
    /// Quantum register of second summand and target; must not be empty.
    internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
        // We are using this version instead of the library version that is based
        // on Fourier angles to show an advantage of sparse simulation in this sample.

        let n = Length(y);
        Fact(n > 0, "Bit width must be at least 1");

        Fact(c >= 0, "constant must not be negative");
        Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");

        if c != 0 {
            // If c has j trailing zeroes than the j least significant bits
            // of y won't be affected by the addition and can therefore be
            // ignored by applying the addition only to the other qubits and
            // shifting c accordingly.
            let j = NTrailingZeroes(c);
            use x = Qubit[n - j];
            within {
                ApplyXorInPlace(c >>> j, x);
            } apply {
                IncByLE(x, y[j...]);
            }
        }
    }

    /// # Summary
    /// Performs greater-than-or-equals comparison to a constant.
    ///
    /// # Description
    /// Toggles output qubit `target` if and only if input register `x`
    /// is greater than or equal to `c`.
    ///
    /// # Input
    /// ## c
    /// Constant value for comparison.
    /// ## x
    /// Quantum register to compare against.
    /// ## target
    /// Target qubit for comparison result.
    ///
    /// # Reference
    /// This construction is described in [Lemma 3, arXiv:2201.10200]
    internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
    : Unit is Adj+Ctl {
        let bitWidth = Length(x);

        if c == 0 {
            X(target);
        } elif c >= 2 ^ bitWidth {
            // do nothing
        } elif c == 2 ^ (bitWidth - 1) {
            ApplyLowTCNOT(Tail(x), target);
        } else {
            // normalize constant
            let l = NTrailingZeroes(c);

            let cNormalized = c >>> l;
            let xNormalized = x[l...];
            let bitWidthNormalized = Length(xNormalized);
            let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));

            use qs = Qubit[bitWidthNormalized - 1];
            let cs1 = [Head(xNormalized)] + Most(qs);
            let cs2 = Rest(xNormalized);

            within {
                for i in IndexRange(gates) {
                    (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
                }
            } apply {
                ApplyLowTCNOT(Tail(qs), target);
            }
        }
    }

    /// # Summary
    /// Internal operation used in the implementation of GreaterThanOrEqualConstant.
    internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
        within {
            ApplyToEachA(X, [control1, control2]);
        } apply {
            ApplyAnd(control1, control2, target);
            X(target);
        }
    }

    internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
    : Unit is Adj {
        body (...) {
            CCNOT(control1, control2, target);
        }
        adjoint (...) {
            H(target);
            if (M(target) == One) {
                X(target);
                CZ(control1, control2);
            }
        }
    }


    /// # Summary
    /// Returns the number of trailing zeroes of a number
    ///
    /// ## Example
    /// ```qsharp
    /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
    /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
    /// ```
    internal function NTrailingZeroes(number : Int) : Int {
        mutable nZeroes = 0;
        mutable copy = number;
        while (copy % 2 == 0) {
            set nZeroes += 1;
            set copy /= 2;
        }
        return nZeroes;
    }

    /// # Summary
    /// An implementation for `CNOT` that when controlled using a single control uses
    /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
    internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
        body (...) {
            CNOT(a, b);
        }

        adjoint self;

        controlled (ctls, ...) {
            // In this application this operation is used in a way that
            // it is controlled by at most one qubit.
            Fact(Length(ctls) <= 1, "At most one control line allowed");

            if IsEmpty(ctls) {
                CNOT(a, b);
            } else {
                use q = Qubit();
                within {
                    ApplyAnd(Head(ctls), a, q);
                } apply {
                    CNOT(q, b);
                }
            }
        }

        controlled adjoint self;
    }

執行資源估算器

資源估算器提供六個預先定義的量子位參數，其中四個具有網關型指令集，以及兩個具有 Majorana 指令集。它也提供兩個量子錯誤修正碼和 surface_code floquet_code。

在此範例中，您會使用 qubit_gate_us_e3 量子位參數和 surface_code 量子錯誤更正碼來執行資源估算器。

選取 [檢視 -> 命令選擇區]，然後輸入「資源」，其中應該會顯示 Q#：計算資源估計 值選項。您也可以從作業前Main顯示的命令清單中按兩下 [估計]。選取此選項以開啟 [資源估算器] 視窗。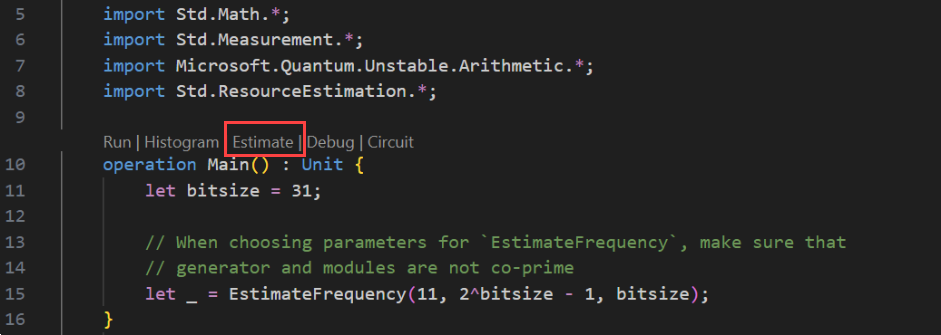
您可以選取一或多個 Qubit 參數 + 錯誤更正碼 類型來估計資源。在此範例中，選取 [qubit_gate_us_e3 ]，然後按兩下 [ 確定]。
指定 錯誤預算 或接受預設值 0.001。在此範例中，保留預設值，然後按 Enter。
按 Enter 以根據檔名接受預設結果名稱，在此案例中為 ShorRE。

查看結果

資源估算器會針對相同的演算法提供多個估計值，每一個都會顯示量子位數目與運行時間之間的取捨。瞭解運行時間與系統規模之間的取捨是資源估計最重要的層面之一。

資源估計的結果會顯示在 [Q# 估計] 視窗中。

[結果] 索引標籤會顯示資源估計的摘要。 按兩下第一個資料列旁的圖示 ，以選取您想要顯示的數據行。您可以從執行名稱、估計類型、量子位類型、qec 配置、錯誤預算、邏輯量子位、邏輯深度、程式代碼距離、T 狀態、T Factory、T Factory 分數、運行時間、rQOPS 和實體量子位中選取。

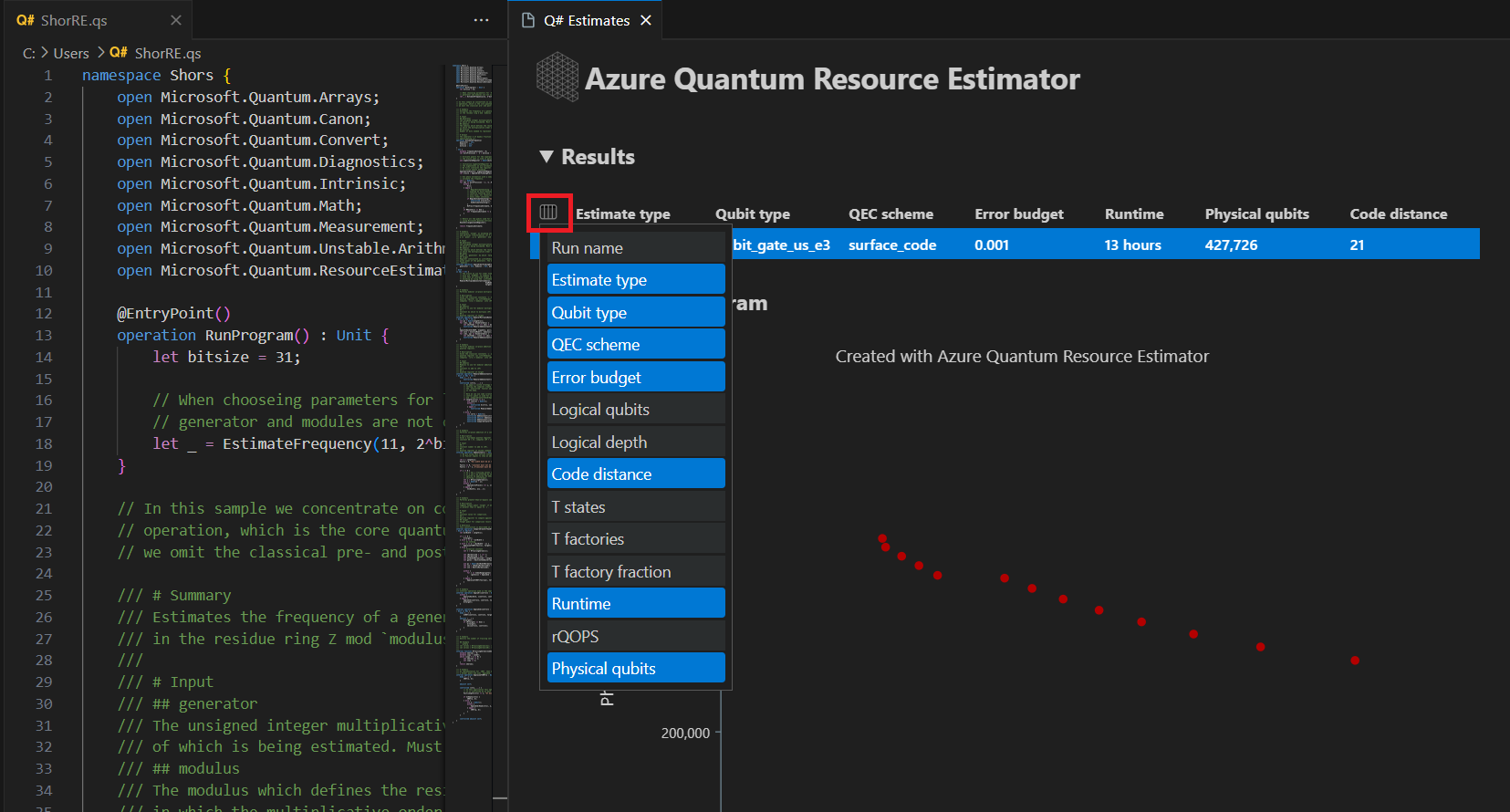
在結果數據表的 [估計類型] 數據行中，您可以看到演算法 {number of qubit， runtime} 的最佳組合數目。這些組合可以在時空圖表中看到。
[時空] 圖表會顯示實體量子位數目與演算法運行時間之間的取捨。在此情況下，資源估算器會從數千個可能的組合中尋找13個不同的最佳組合。您可以將滑鼠停留在每個 {number of qubits， runtime} 點上，以查看該時間點的資源估計詳細數據。

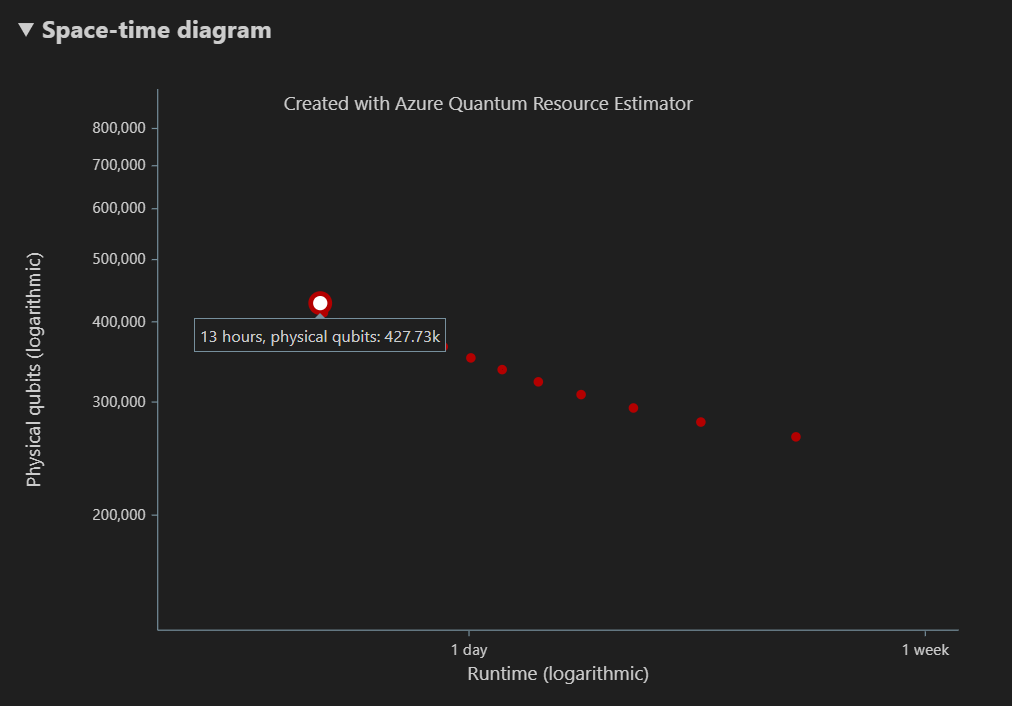
如需詳細資訊，請參閱時空圖表。

注意

您必須 按下某一個空格時間圖表的點 ，也就是 {number of qubits， runtime} pair，以查看空間圖表，以及對應至該點的資源估計詳細數據。
空間圖顯示演算法和 T Factory 所使用的實體量子位分佈，對應至 {number of qubit， runtime} 組。例如，如果您在時空圖中選取最左邊的點，則執行演算法所需的實體量子位數目427726，其中196686為演算法量子位，其中 231040 為 T Factory 量子位。

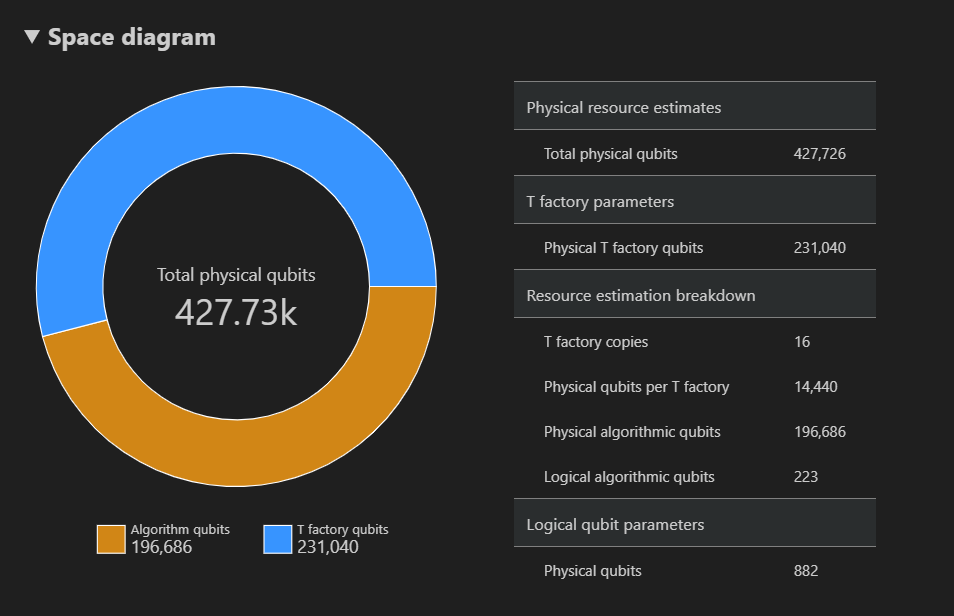
最後，[ 資源估計 值] 索引卷標會顯示對應至 {number of qubits， runtime} 配對之資源估算器輸出數據的完整清單。您可以藉由折迭群組來檢查成本詳細資料，這些群組具有詳細資訊。例如，選取時空圖表中最左邊的點，然後折疊 邏輯量子位參數 群組。

邏輯量子位元參數	值
QEC 配置	surface_code
程式碼距離	21
實際量子位元	882
邏輯週期時間	13 毫秒
邏輯量子位元錯誤率	3.00E-13
交叉前置要素	0.03
錯誤修正臨界值	0.01
邏輯週期時間公式	(4 * `twoQubitGateTime` + 2 * `oneQubitMeasurementTime`) * `codeDistance`
實體量子位元公式	2 * `codeDistance` * `codeDistance`

提示

按兩下 [ 顯示詳細資料列 ] 以顯示報表資料之每個輸出的描述。

如需詳細資訊，請參閱資源估算器的完整報表數據。

target變更參數

您可以使用其他量子位類型、錯誤更正碼和錯誤預算來估計相同 Q# 程式的成本。選取 [檢視 -> 命令選擇區]，然後輸入 Q#: Calculate Resource Estimates，以開啟 [資源估算器] 視窗。

選取任何其他組態，例如 Majorana 型量子位參數 qubit_maj_ns_e6。接受預設錯誤預算值或輸入新的值，然後按 Enter 鍵。資源估算器會使用新的 target 參數重新執行估計。

如需詳細資訊，請參閱 Target 資源估算器的參數。

執行多個參數位列態

Azure Quantum 資源估算器可以執行多個參數位列態 target ，並比較資源估計結果。

選取 [檢視 -> 命令選擇區]，或按 Ctrl+Shift+P，然後輸入 Q#: Calculate Resource Estimates。
選取 [qubit_gate_us_e3]、 [qubit_gate_us_e4]、 [qubit_maj_ns_e4 + floquet_code] 和 [qubit_maj_ns_e6 + floquet_code]，然後按兩下 [ 確定]。
接受預設錯誤預算值 0.001，然後按 Enter。
按 Enter 以接受輸入檔，在此案例中為 ShorRE.qs。
如果是多個參數位列態，結果會顯示在 [結果] 索引卷標的不同數據列中。
[ 時空] 圖表 會顯示所有參數位列態的結果。結果數據表的第一個數據行會顯示每個參數位態的圖例。您可以將滑鼠停留在每個點上，以查看該時間點的資源估計詳細數據。
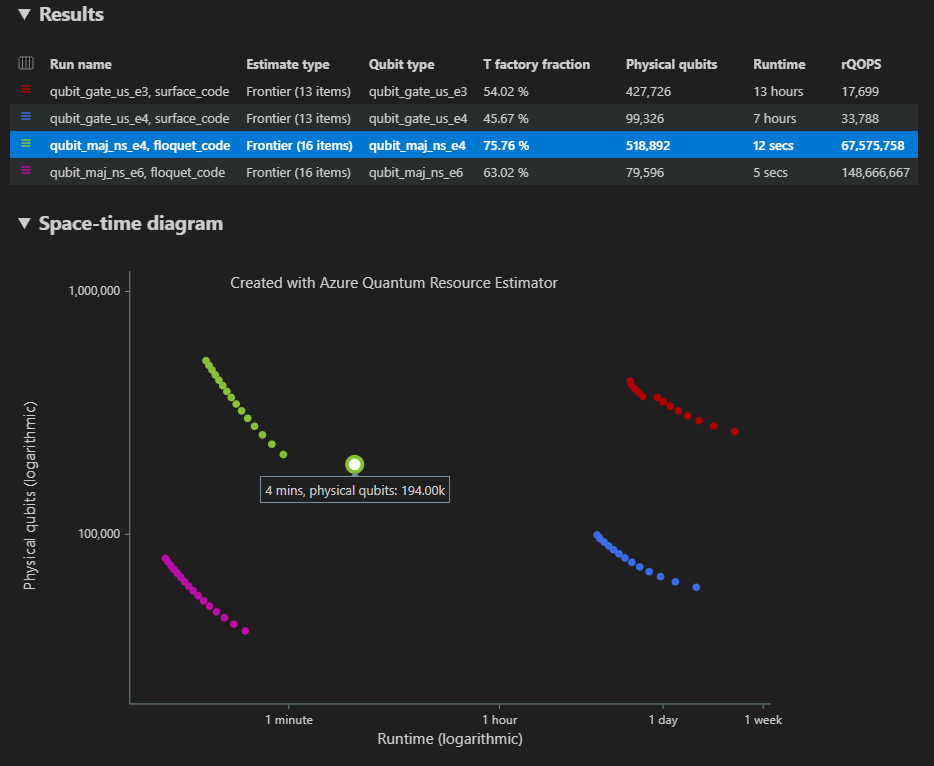
按兩下 空格時間圖表的 {number of qubits， runtime} 點 ，以顯示對應的空間圖表和報表數據。

VS Code 中 Jupyter Notebook 的必要條件

已安裝 Python 和 Pip 的 Python 環境。
最新版的 Visual Studio Code 或開啟 Web上的 VS Code。
已安裝 Azure Quantum Development Kit、 Python 和 Jupyter 擴充功能的 VS Code。

最新的 Azure Quantum qsharp 和 qsharp-widgets 套件。

python -m pip install --upgrade qsharp qsharp-widgets

提示

您不需要有 Azure 帳戶來執行本機資源估算器。

建立量子演算法

在 VS Code 中，選取 [檢視]>[命令選擇區]，然後選取 [建立:新增 Jupyter Notebook]。
在右上方，VS Code 會偵測並顯示針對筆記本選取的 Python 版本和虛擬 Python 環境。如果您有多個 Python 環境，您可能需要使用右上方的核心選擇器來選取核心。如果未偵測到任何環境，請參閱 VS Code 中的 Jupyter Notebook 以取得設定資訊。
在筆記本的第一個儲存格中，匯入 qsharp 套件。
```
import qsharp
```

新增儲存格並複製下列程式碼。

%%qsharp
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;

operation RunProgram() : Unit {
    let bitsize = 31;

    // When choosing parameters for `EstimateFrequency`, make sure that
    // generator and modules are not co-prime
    let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}


// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.

/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
    generator : Int,
    modulus : Int,
    bitsize : Int
)
: Int {
    mutable frequencyEstimate = 0;
    let bitsPrecision =  2 * bitsize + 1;

    // Allocate qubits for the superposition of eigenstates of
    // the oracle that is used in period finding.
    use eigenstateRegister = Qubit[bitsize];

    // Initialize eigenstateRegister to 1, which is a superposition of
    // the eigenstates we are estimating the phases of.
    // We first interpret the register as encoding an unsigned integer
    // in little endian encoding.
    ApplyXorInPlace(1, eigenstateRegister);
    let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);

    // Use phase estimation with a semiclassical Fourier transform to
    // estimate the frequency.
    use c = Qubit();
    for idx in bitsPrecision - 1..-1..0 {
        within {
            H(c);
        } apply {
            // `BeginEstimateCaching` and `EndEstimateCaching` are the operations
            // exposed by Azure Quantum Resource Estimator. These will instruct
            // resource counting such that the if-block will be executed
            // only once, its resources will be cached, and appended in
            // every other iteration.
            if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
                Controlled oracle([c], (1 <<< idx, eigenstateRegister));
                EndEstimateCaching();
            }
            R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
        }
        if MResetZ(c) == One {
            set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
        }
    }

    // Return all the qubits used for oracle eigenstate back to 0 state
    // using Microsoft.Quantum.Intrinsic.ResetAll.
    ResetAll(eigenstateRegister);

    return frequencyEstimate;
}

/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
    generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
    // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
    // also use `ExpModI` to compute a by which x must be multiplied. Also
    // note that we interpret target as unsigned integer in little-endian
    // encoding.
    ModularMultiplyByConstant(modulus,
                                ExpModI(generator, power, modulus),
                                target);
}

/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
    use qs = Qubit[Length(y)];
    for (idx, yq) in Enumerated(y) {
        let shiftedC = (c <<< idx) % modulus;
        Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
    }
    ApplyToEachCA(SWAP, Zipped(y, qs));
    let invC = InverseModI(c, modulus);
    for (idx, yq) in Enumerated(y) {
        let shiftedC = (invC <<< idx) % modulus;
        Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
    }
}

/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register  |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
    body (...) {
        Controlled ModularAddConstant([], (modulus, c, y));
    }
    controlled (ctrls, ...) {
        // We apply a custom strategy to control this operation instead of
        // letting the compiler create the controlled variant for us in which
        // the `Controlled` functor would be distributed over each operation
        // in the body.
        //
        // Here we can use some scratch memory to save ensure that at most one
        // control qubit is used for costly operations such as `AddConstant`
        // and `CompareGreaterThenOrEqualConstant`.
        if Length(ctrls) >= 2 {
            use control = Qubit();
            within {
                Controlled X(ctrls, control);
            } apply {
                Controlled ModularAddConstant([control], (modulus, c, y));
            }
        } else {
            use carry = Qubit();
            Controlled AddConstant(ctrls, (c, y + [carry]));
            Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
            Controlled AddConstant([carry], (modulus, y));
            Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
        }
    }
}

/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
    // We are using this version instead of the library version that is based
    // on Fourier angles to show an advantage of sparse simulation in this sample.

    let n = Length(y);
    Fact(n > 0, "Bit width must be at least 1");

    Fact(c >= 0, "constant must not be negative");
    Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");

    if c != 0 {
        // If c has j trailing zeroes than the j least significant bits
        // of y will not be affected by the addition and can therefore be
        // ignored by applying the addition only to the other qubits and
        // shifting c accordingly.
        let j = NTrailingZeroes(c);
        use x = Qubit[n - j];
        within {
            ApplyXorInPlace(c >>> j, x);
        } apply {
            IncByLE(x, y[j...]);
        }
    }
}

/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
    let bitWidth = Length(x);

    if c == 0 {
        X(target);
    } elif c >= 2 ^ bitWidth {
        // do nothing
    } elif c == 2 ^ (bitWidth - 1) {
        ApplyLowTCNOT(Tail(x), target);
    } else {
        // normalize constant
        let l = NTrailingZeroes(c);

        let cNormalized = c >>> l;
        let xNormalized = x[l...];
        let bitWidthNormalized = Length(xNormalized);
        let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));

        use qs = Qubit[bitWidthNormalized - 1];
        let cs1 = [Head(xNormalized)] + Most(qs);
        let cs2 = Rest(xNormalized);

        within {
            for i in IndexRange(gates) {
                (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
            }
        } apply {
            ApplyLowTCNOT(Tail(qs), target);
        }
    }
}

/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
    within {
        ApplyToEachA(X, [control1, control2]);
    } apply {
        ApplyAnd(control1, control2, target);
        X(target);
    }
}

internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
    body (...) {
        CCNOT(control1, control2, target);
    }
    adjoint (...) {
        H(target);
        if (M(target) == One) {
            X(target);
            CZ(control1, control2);
        }
    }
}


/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
    mutable nZeroes = 0;
    mutable copy = number;
    while (copy % 2 == 0) {
        set nZeroes += 1;
        set copy /= 2;
    }
    return nZeroes;
}

/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
    body (...) {
        CNOT(a, b);
    }

    adjoint self;

    controlled (ctls, ...) {
        // In this application this operation is used in a way that
        // it is controlled by at most one qubit.
        Fact(Length(ctls) <= 1, "At most one control line allowed");

        if IsEmpty(ctls) {
            CNOT(a, b);
        } else {
            use q = Qubit();
            within {
                ApplyAnd(Head(ctls), a, q);
            } apply {
                CNOT(q, b);
            }
        }
    }

    controlled adjoint self;
}

估計量子演算法

現在，您會使用預設假設來估計 RunProgram 作業的實體資源。新增儲存格並複製下列程式碼。

result = qsharp.estimate("RunProgram()")
result

qsharp.estimate 函式會建立結果物件，可用來顯示具有整體實體資源計數的資料表。您可以藉由折迭群組來檢查成本詳細資料，這些群組具有詳細資訊。如需詳細資訊，請參閱資源估算器的完整報表數據。

例如，摺疊 [邏輯量子位元參數] 群組，以查看程式碼距離為 21，而實體量子位元的數目為 882。

邏輯量子位元參數	值
QEC 配置	surface_code
程式碼距離	21
實際量子位元	882
邏輯週期時間	8 千米
邏輯量子位元錯誤率	3.00E-13
交叉前置要素	0.03
錯誤修正臨界值	0.01
邏輯週期時間公式	(4 * `twoQubitGateTime` + 2 * `oneQubitMeasurementTime`) * `codeDistance`
實體量子位元公式	2 * `codeDistance` * `codeDistance`

提示

如需更精簡的輸出資料表版本，您可以使用 result.summary。

空間圖

演算法和 T Factory 所使用的實體量子位元分佈是可能會影響演算法設計的因素。您可以使用 qsharp-widgets 套件將此分佈視覺化，以進一步了解演算法的估計空間需求。

from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)

在此範例中，執行演算法所需的實體量子位元數目 829766，其中 196686 為演算法量子位元，而其中 633080 為 T Factory 量子位元。

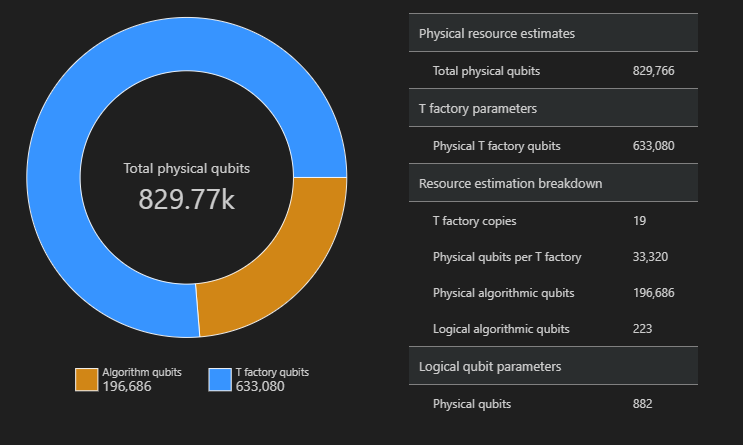
顯示資源估算器空間圖的螢幕快照。

變更預設值並估計演算法

提交計劃的資源估計要求時，您可以指定一些選擇性參數。 jobParams使用欄位來存取可傳遞至作業執行的所有target參數，並查看假設的預設值：

result['jobParams']

{'errorBudget': 0.001,
 'qecScheme': {'crossingPrefactor': 0.03,
  'errorCorrectionThreshold': 0.01,
  'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
  'name': 'surface_code',
  'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
 'qubitParams': {'instructionSet': 'GateBased',
  'name': 'qubit_gate_ns_e3',
  'oneQubitGateErrorRate': 0.001,
  'oneQubitGateTime': '50 ns',
  'oneQubitMeasurementErrorRate': 0.001,
  'oneQubitMeasurementTime': '100 ns',
  'tGateErrorRate': 0.001,
  'tGateTime': '50 ns',
  'twoQubitGateErrorRate': 0.001,
  'twoQubitGateTime': '50 ns'}}

您可以看到資源估算器會採用 qubit_gate_ns_e3 量子位模型、surface_code 錯誤更正碼和 0.001 錯誤預算作為估計的預設值。

以下是 target 可自訂的參數：

errorBudget - 演算法的整體允許錯誤預算
qecScheme - 量子誤差修正 (QEC) 配置
qubitParams - 實體量子位元參數
constraints - 元件層級的條件約束
distillationUnitSpecifications - T Factory 擷取演算法的規格。
estimateType - 單一或前沿

如需詳細資訊，請參閱 Target 資源估算器的參數。

變更量子位元模型

您可以使用以 Majorana 為基礎的量子位元參數，qubitParams，「qubit_maj_ns_e6」來估計相同演算法的成本。

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                }})
EstimateDetails(result_maj)

變更量子誤差修正配置

您可以在 Majorana 型的量子位元參數上，使用浮點 QEC 配置，qecScheme，重新執行相同範例的資源估計作業。

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                },
                "qecScheme": {
                    "name": "floquet_code"
                }})
EstimateDetails(result_maj)

變更錯誤預算

接下來，使用 10% 的 errorBudget，重新執行相同的量子線路。

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                },
                "qecScheme": {
                    "name": "floquet_code"
                },
                "errorBudget": 0.1})
EstimateDetails(result_maj)

使用資源估算器進行批處理

Azure Quantum 資源估算器可讓您執行多個參陣列 target 態，並比較結果。當您想要比較不同量子位元模型、QEC 配置或錯誤預算的成本時，這會很有用。

您可以將參數清單 target 傳遞至 params 函式的參數 qsharp.estimate ，以執行批次估計。例如，使用預設參數和以 Majorana 為基礎的量子位參數搭配 floquet QEC 配置來執行相同的演算法。

result_batch = qsharp.estimate("RunProgram()", params=
                [{}, # Default parameters
                {
                    "qubitParams": {
                        "name": "qubit_maj_ns_e6"
                    },
                    "qecScheme": {
                        "name": "floquet_code"
                    }
                }])
result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])

Model	邏輯量子位元	邏輯深度	T 狀態	程式碼距離	T Factory	T Factory 分數	實際量子位元	rQOPS	實際執行時間
閘道型 ns, 10⁻³	223	3.64M	4.70M	21	19	76.30 %	829.77k	26.55M	31 秒
Majorana ns, 10⁻⁶	223	3.64M	4.70M	5	19	63.02 %	79.60k	148.67M	5 secs

您也可以使用 EstimatorParams 類別來建構估計參數清單。

from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts

labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]

params = EstimatorParams(num_items=6)
params.error_budget = 0.333
params.items[0].qubit_params.name = QubitParams.GATE_US_E3
params.items[1].qubit_params.name = QubitParams.GATE_US_E4
params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE

qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)

Model	邏輯量子位元	邏輯深度	T 狀態	程式碼距離	T Factory	T Factory 分數	實際量子位元	rQOPS	實際執行時間
閘道型 µs, 10⁻³	223 3.64M	4.70M	17	13	40.54 %	216.77k	21.86k	10 個小時
閘道型 µs, 10⁻⁴	223	3.64M	4.70M	9	14	43.17 %	63.57k	41.30k	5 個小時
閘道型 ns, 10⁻³	223 3.64M	4.70M	17	16	69.08 %	416.89k	32.79M	25 secs
閘道型 ns, 10⁻⁴	223 3.64M	4.70M	9	14	43.17 %	63.57k	61.94M	13 secs
Majorana ns, 10⁻⁴	223 3.64M	4.70M	9	19	82.75 %	501.48k	82.59M	10 secs
Majorana ns, 10⁻⁶	223 3.64M	4.70M	5	13	31.47 %	42.96k	148.67M	5 secs

執行 Pareto 邊境估計

評估演算法的資源時，請務必考慮實體量子位數目與演算法運行時間之間的取捨。您可以考慮盡可能配置盡可能多的實體量子位，以減少演算法的運行時間。不過，實體量子位的數目會受限於量子硬體中可用的實體量子位數目。

Pareto 前沿估計會為相同的演算法提供多個估計值，每個演算法在量子位數目與運行時間之間都有取捨。

若要使用 Pareto 邊際估計來執行資源估算器，您必須將參數指定 "estimateType"target 為 "frontier"。例如，使用以Majorana為基礎的量子位參數搭配使用Pareto邊界估計，使用表面程式代碼執行相同的演算法。

result = qsharp.estimate("RunProgram()", params=
                            {"qubitParams": { "name": "qubit_maj_ns_e4" },
                            "qecScheme": { "name": "surface_code" },
                            "estimateType": "frontier", # frontier estimation
                            }
                        )

您可以使用函 EstimatesOverview 式來顯示具有整體實體資源計數的數據表。按兩下第一個資料列旁的圖示，以選取您想要顯示的數據行。您可以從執行名稱、估計類型、量子位類型、qec 配置、錯誤預算、邏輯量子位、邏輯深度、程式代碼距離、T 狀態、T Factory、T Factory 分數、運行時間、rQOPS 和實體量子位中選取。
```
from qsharp_widgets import EstimatesOverview
EstimatesOverview(result)
```

在結果數據表的 [ 估計類型 ] 數據行中，您可以看到演算法 {number of qubits， runtime} 的不同組合數目。在此情況下，資源估算器會找出數千個可能組合的 22 個不同最佳組合。

時空圖表

函式 EstimatesOverview 也會顯示資源估算器的空間時程圖表。

時空圖顯示每個 {量子位、運行時間} 組的實體量子位數目和演算法運行時間。您可以將滑鼠停留在每個點上，以查看該時間點的資源估計詳細數據。

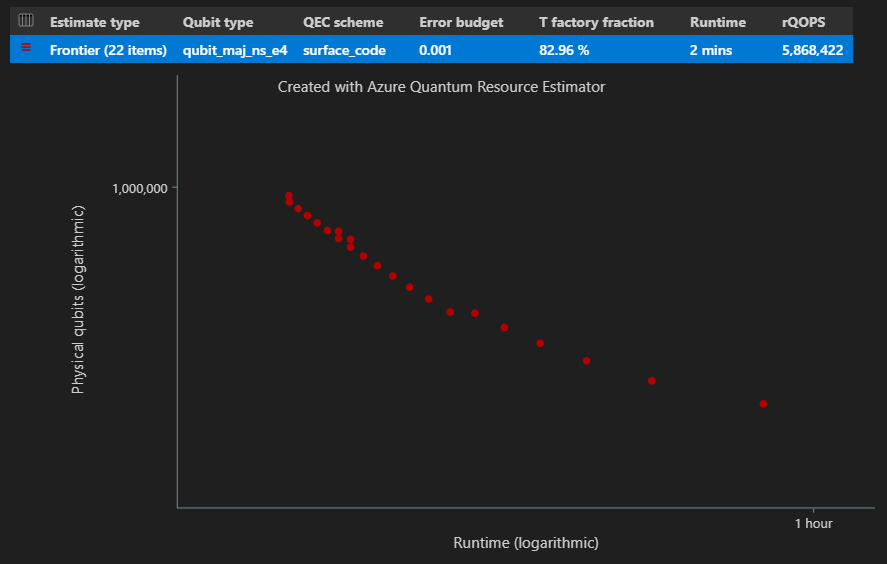
此螢幕快照顯示具有資源估算器邊界估計的時空圖表。

使用 Pareto 邊境估計進行批處理

若要估計和比較多個參數位列 target 態與前沿估計，請將新增 "estimateType": "frontier", 至參數。

result = qsharp.estimate(
    "RunProgram()",
    [
        {
        "qubitParams": { "name": "qubit_maj_ns_e4" },
        "qecScheme": { "name": "surface_code" },
        "estimateType": "frontier", # Pareto frontier estimation
        },
        {
        "qubitParams": { "name": "qubit_maj_ns_e6" },
        "qecScheme": { "name": "floquet_code" },
        "estimateType": "frontier", # Pareto frontier estimation
        },
    ]
)

EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])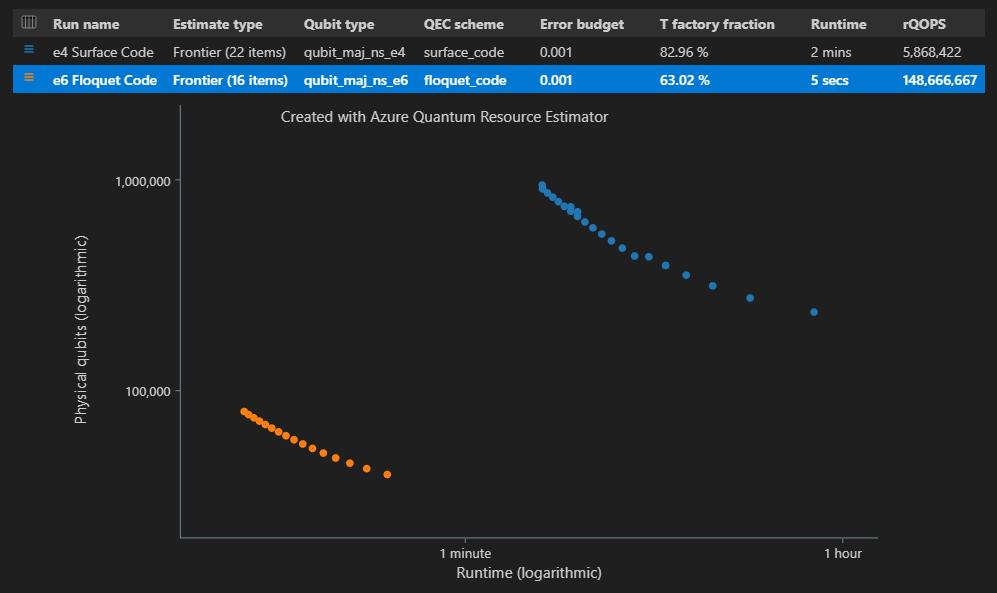

此螢幕快照顯示使用Pareto邊界估計和多個參數位態時，資源估算器的空間圖表。

注意

您可以使用函式來定義量子位時間圖表 EstimatesOverview 的色彩和執行名稱。

使用 Pareto 邊界估計執行多個參數組 target 態時，您可以看到空間時程圖表特定時間點的資源估計值，也就是每個 {量子位數目、運行時間} 組。例如，下列程式代碼會顯示第二個（estimate index=0） run 和第四個（point index=3）最短運行時間的估計詳細數據使用量。
```
EstimateDetails(result[1], 4)
```
您也可以查看空間圖中特定時間點的空間圖表。例如，下列程式代碼顯示組合第一次執行的空間圖表（estimate index=0）和第三個最短運行時間（point index=2）。
```
SpaceChart(result[0], 2)
```

Qiskit 的必要條件

具有有效訂用帳戶的 Azure 帳戶。如果您沒有 Azure 帳戶，請免費註冊並註冊隨用隨付訂用帳戶。
Azure Quantum 工作區。如需詳細資訊，請參閱建立 Azure Quantum 工作區。

在您的工作區中啟用 Azure Quantum 資源估算器target

資源估算器是 target Microsoft Quantum Computing 提供者的。如果您在資源估算器發行后已建立工作區，則會自動將Microsoft Quantum Computing 提供者新增至您的工作區。

如果您使用 現有的 Azure Quantum 工作區：

在 Azure 入口網站中開啟您的工作區。
在左側面板的 [作業] 底下，選取 [提供者]。
選取 [+ 新增提供者]。
針對 Microsoft Quantum Computing 選取 [+ 新增]。
選取 [ 學習與開發 ]，然後選取 [ 新增]。

在工作區中建立新的筆記本

登入 Azure 入口網站，並選取您的 Azure Quantum 工作區。
在 [作業] 底下，選取 [筆記本]
按兩下 [我的筆記本] ，然後按兩下 [ 新增]
在 [核心類型]中，選取 [IPython]。
輸入檔案的名稱，然後按兩下 [ 建立檔案]。

當您的新筆記本開啟時，會根據您的訂用帳戶和工作區資訊自動建立第一個儲存格的程式碼。

from azure.quantum import Workspace
workspace = Workspace ( 
    resource_id = "", # Your resource_id 
    location = ""  # Your workspace location (for example, "westus") 
)

注意

除非另有說明，否則您應該在建立數據格時依序執行每個數據格，以避免發生任何編譯問題。

按兩下單元格左邊的三角形「播放」圖示，以執行程式碼。

載入必要的匯入

首先，您必須從 azure-quantum 和 qiskit匯入額外的模組。

單擊 [+ 程式代碼 ] 以新增儲存格，然後新增並執行下列程式代碼：

from azure.quantum.qiskit import AzureQuantumProvider
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import RGQFTMultiplier

聯機到 Azure Quantum 服務

接下來，使用workspace上一個單元格中的物件來建立 AzureQuantumProvider 物件，以連線到您的 Azure Quantum 工作區。您可以建立後端實例，並將資源估算器設定為 target。

provider = AzureQuantumProvider(workspace)
backend = provider.get_backend('microsoft.estimator')

建立量子演算法

在此範例中，您會根據 Ruiz-Perez 和 Garcia-Escartin （arXiv：1411.5949）中呈現的建構來建立乘數的量子電路，其使用 Quantum Fourier Transform 來實作算術。

您可以藉由變更 bitwidth 變數來調整乘數的大小。線路產生會包裝在可使用 bitwidth 乘數值呼叫的函式中。此作業會有兩個輸入緩存器，每個輸入緩存器的大小都是指定的 bitwidth，而一個輸出緩存器的大小是指定 bitwidth的大小兩倍。函式也會列印直接從量子電路擷取之乘數的一些邏輯資源計數。

def create_algorithm(bitwidth):
    print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
    
    # Print a warning for large bitwidths that will require some time to generate and
    # transpile the circuit.
    if bitwidth > 18:
        print(f"[WARN] It will take more than one minute generate a quantum circuit with a bitwidth larger than 18")

    circ = RGQFTMultiplier(num_state_qubits=bitwidth, num_result_qubits=2 * bitwidth)

    # One could further reduce the resource estimates by increasing the optimization_level,
    # however, this will also increase the runtime to construct the algorithm.  Note, that
    # it does not affect the runtime for resource estimation.
    print(f"[INFO] Decompose circuit into intrinsic quantum operations")

    circ = transpile(circ, basis_gates=SUPPORTED_INSTRUCTIONS, optimization_level=0)

    # print some statistics
    print(f"[INFO]   qubit count: {circ.num_qubits}")
    print("[INFO]   gate counts")
    for gate, count in circ.count_ops().items():
        print(f"[INFO]   - {gate}: {count}")

    return circ

注意

您可以針對沒有 T 狀態，但至少有一個測量的演算法提交實體資源估計作業。

估計量子演算法

使用函 create_algorithm 式建立演算法的實例。您可以藉由變更 bitwidth 變數來調整乘數的大小。

bitwidth = 4

circ = create_algorithm(bitwidth)

使用預設假設估計此作業的實體資源。您可以使用方法將線路提交至資源估算器後端 run ，然後執行 job.result() 以等候作業完成並傳回結果。

job = backend.run(circ)
result = job.result()
result

這會建立顯示整體實體資源計數的數據表。您可以藉由折迭群組來檢查成本詳細資料，這些群組具有詳細資訊。

提示

如需更精簡的輸出資料表版本，您可以使用 result.summary。

例如，如果您折疊 邏輯量子位參數 群組，您可以更輕鬆地看到錯誤更正碼距離是 15。

邏輯量子位元參數	值
QEC 配置	surface_code
程式碼距離	15
實際量子位元	450
邏輯週期時間	6us
邏輯量子位元錯誤率	3.00E-10
交叉前置要素	0.03
錯誤修正臨界值	0.01
邏輯週期時間公式	(4 * `twoQubitGateTime` + 2 * `oneQubitMeasurementTime`) * `codeDistance`
實體量子位元公式	2 * `codeDistance` * `codeDistance`

在實體 量子位參數 群組中，您可以看到針對此估計所假設的實體量子位屬性。例如，分別假設執行單一量子位測量和單一量子位閘道的時間是 100 奈秒和 50 奈秒。

提示

您也可以使用 result.data（）方法，以 Python 字典的形式存取資源估算器的輸出。

如需詳細資訊，請參閱資源估算器的完整輸出數據清單。

空間圖

演算法和 T Factory 所使用的實體量子位元分佈是可能會影響演算法設計的因素。您可以將此分佈可視化，以進一步瞭解演算法的估計空間需求。

result.diagram.space

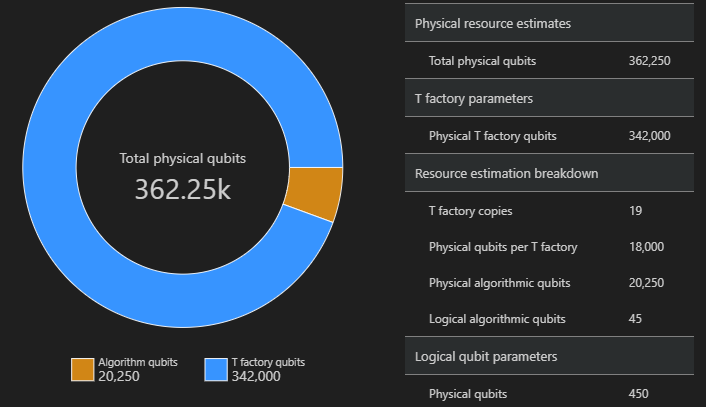
餅圖顯示演算法量子位與 T Factory 量子位之間的實體量子位總計分佈。有一個數據表，其中包含 T 處理站複本數目和每個 T Factory 的實體量子位數目。

空間圖顯示演算法量子位和 T Factory 量子位的比例。請注意，T Factory 復本數目為 28，會貢獻 T Factory 的實體量子位數目，因為 $\text{T factoryies} \cdot \text{physical qubit per T factory}= 28 \cdot 18,000 = 504,000$。

如需詳細資訊，請參閱 T Factory 實體估計。

變更預設值並估計演算法

提交計劃的資源估計要求時，您可以指定一些選擇性參數。 jobParams使用欄位來存取可傳遞至作業執行的所有值，並查看假設的預設值：

result.data()["jobParams"]

{'errorBudget': 0.001,
 'qecScheme': {'crossingPrefactor': 0.03,
  'errorCorrectionThreshold': 0.01,
  'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
  'name': 'surface_code',
  'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
 'qubitParams': {'instructionSet': 'GateBased',
  'name': 'qubit_gate_ns_e3',
  'oneQubitGateErrorRate': 0.001,
  'oneQubitGateTime': '50 ns',
  'oneQubitMeasurementErrorRate': 0.001,
  'oneQubitMeasurementTime': '100 ns',
  'tGateErrorRate': 0.001,
  'tGateTime': '50 ns',
  'twoQubitGateErrorRate': 0.001,
  'twoQubitGateTime': '50 ns'}}

以下是 target 可自訂的參數：

errorBudget - 整體允許的錯誤預算
qecScheme - 量子誤差修正 (QEC) 配置
qubitParams - 實體量子位元參數
constraints - 元件層級的條件約束
distillationUnitSpecifications - T Factory 擷取演算法的規格。

如需詳細資訊，請參閱 Target 資源估算器的參數。

變更量子位元模型

接下來，使用Majorana型量子位參數估計相同演算法的成本 qubit_maj_ns_e6

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    })
result = job.result()
result

您可以以程式設計方式檢查實體計數。例如，您可以探索建立以執行演算法之 T Factory 的詳細數據。

result.data()["tfactory"]

{'eccDistancePerRound': [1, 1, 5],
 'logicalErrorRate': 1.6833177305222897e-10,
 'moduleNamePerRound': ['15-to-1 space efficient physical',
  '15-to-1 RM prep physical',
  '15-to-1 RM prep logical'],
 'numInputTstates': 20520,
 'numModulesPerRound': [1368, 20, 1],
 'numRounds': 3,
 'numTstates': 1,
 'physicalQubits': 16416,
 'physicalQubitsPerRound': [12, 31, 1550],
 'runtime': 116900.0,
 'runtimePerRound': [4500.0, 2400.0, 110000.0]}

注意

根據預設，運行時間會顯示在 nanoseconds 中。

您可以使用此資料來產生 T Factory 如何產生必要 T 狀態的一些說明。

data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]

print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
    print(f"""- {tfactory["numModulesPerRound"][round]} {tfactory["moduleNamePerRound"][round]} unit(s)""")

A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)

變更量子誤差修正配置

現在，針對以 Majorana 為基礎的量子位參數，使用已壓縮的 QEC 配置，重新執行相同範例的資源估計作業。 qecScheme

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    },
    qecScheme={
        "name": "floquet_code"
    })
result_maj_floquet = job.result()
result_maj_floquet

變更錯誤預算

讓我們以 10% 的來重新執行相同的量子線路 errorBudget 。

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    },
    qecScheme={
        "name": "floquet_code"
    },
    errorBudget=0.1)
result_maj_floquet_e1 = job.result()
result_maj_floquet_e1

注意

如果您在使用資源估算器時遇到任何問題，請參閱疑難解答頁面，或連絡 AzureQuantumInfo@microsoft.com。

共用方式為

執行資源估算器的不同方式

VS Code 的必要條件

建立新的 Q# 檔案

建立量子演算法

執行資源估算器

查看結果

target變更參數

執行多個參數位列態

VS Code 中 Jupyter Notebook 的必要條件

建立量子演算法

估計量子演算法

空間圖

變更預設值並估計演算法

變更量子位元模型

變更量子誤差修正配置

變更錯誤預算

使用資源估算器進行批處理

執行 Pareto 邊境估計

時空圖表

使用 Pareto 邊境估計進行批處理

Qiskit 的必要條件

在您的工作區中啟用 Azure Quantum 資源估算器target

在工作區中建立新的筆記本

載入必要的匯入

聯機到 Azure Quantum 服務

建立量子演算法

估計量子演算法

空間圖

變更預設值並估計演算法

變更量子位元模型

變更量子誤差修正配置

變更錯誤預算

下一步

意見反應

其他資源