附录:矩阵转换
本主题提供二维图形矩阵转换的数学概述。 但是,无需知道矩阵数学,才能在 Direct2D 中使用转换。 如果你对数学感兴趣,请阅读本主题;否则,请随意跳过本主题。
矩阵简介
矩阵是实数的矩形数组。 矩阵的 顺序 是行数和列数。 例如,如果矩阵有 3 行和 2 列,则顺序为 3 × 2。 矩阵通常用方括号括起来的矩阵元素显示:

表示法:矩阵由大写字母指定。 元素由小写字母指定。 下标指示元素的行号和列号。 例如,ij 是矩阵 A 的第 i 行和第 j 列的元素。
下图显示了一个 i × j 矩阵,其中包含矩阵的每个单元格中的单个元素。

矩阵作
本部分介绍在矩阵上定义的基本作。
添加。 通过添加 A 和 B 的相应元素来获取两个矩阵的 A + B 的总和:
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
标量乘法。 此作将矩阵乘以实数。 给定实数 k,则通过乘以 A 的每个元素乘以 k来获取标量积 kA。
- kA = k\[ a*ij* \] = \[ k ×*ij* \]
矩阵乘法。 假设有两个矩阵 A 和 B(m × n) 和 (n × p),则 product C = A × B 是一个矩阵,其顺序为 m × p),定义如下:
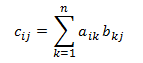
或者,等效:
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*
也就是说,若要计算每个元素 cij,请执行以下作:
- 获取 A 的第一行和 B 的第 j 列。
- 将行和列中的每一对元素相乘:第一行项按第一列项、第二行项乘以第二列项,依此类推。
- 对结果求和。
下面是将一个矩阵(2 × 2)矩阵乘以(2 × 3)矩阵的示例。
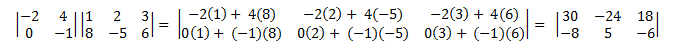
矩阵乘法不是通勤的。 也就是说,A × B ≠ B × A。此外,从定义中,它遵循的不是每对矩阵都可以相乘。 左侧矩阵中的列数必须等于右侧矩阵中的行数。 否则,未定义×运算符。
标识矩阵。 标识矩阵(指定 I)是一个定义如下的平方矩阵:
- 如果 *i* = *j*,则 I*ij* = 1;否则为 0。
换句话说,标识矩阵包含每个元素的 1,其中行号等于列号,对于所有其他元素,则为零。 例如,下面是 3 个× 3 个标识矩阵。
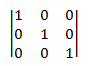
任何矩阵 M 的以下相等性保留。
- M x I = M I x M = M
Affine Transforms
相交转换 是一种数学运算,用于将一个坐标空间映射到另一个坐标空间。 换句话说,它将一组点映射到另一组点。 Affine 转换具有一些功能,使它们在计算机图形中很有用。
- Affine 转换将保留 对等性。 如果三个或更多个点落在一行上,它们仍然在转换后形成一条线。 直线保持直线。
- 两个相交转换的构成是一个相交转换。
二维空间的 Affine 转换具有以下形式。
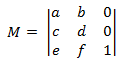
如果应用前面给出的矩阵乘法的定义,则可以显示两个相交转换的乘积是另一个相交转换。 若要使用相交转换转换 2D 点,该点表示为 1 × 3 矩阵。
- P = \|x y 1 \|
前两个元素包含点的 x 和 y 坐标。 1 放置在第三个元素中,使数学正常工作。 若要应用转换,请按如下所示将两个矩阵相乘。
- P' = P × M
这会扩展到以下内容。
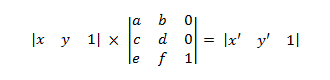
哪里
- x' = ax + cy + e y' = bx + dy + f
若要获取转换的点,请获取矩阵 P'的前两个元素。
- p = (x', y') = (ax + cy + e, bx + dy + f)
注意
1 × n 矩阵称为 行向量。 Direct2D 和 Direct3D 都使用行向量来表示 2D 或 3D 空间中的点。 可以使用列向量(n × 1)并转置转换矩阵来获取等效的结果。 大多数图形文本都使用列向量形式。 本主题介绍行向量形式,以便与 Direct2D 和 Direct3D 保持一致。
接下来的几个部分派生基本转换。
转换转换
转换转换矩阵采用以下形式。
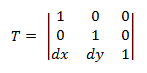
将点 P 插入此公式生成:
- P' = (*x* + *dx*, *y* + *dy*)
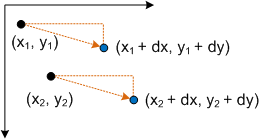
对应于 X 轴中的 dx dx 翻译的点(x,y),Y 轴中的 dy。
缩放转换
缩放转换矩阵具有以下形式。
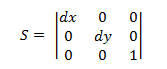
将点 P 插入此公式生成:
- P' = (*x* \ *dx*, *y* \ *dy*)
对应于 dx 和 dy缩放的点(x,y)。

围绕原点旋转
在原点周围旋转点的矩阵具有以下形式。

转换的点为:
- P' = (*x*cos≤ – ysin≤、*x*sin≤ + *y*cos 菲尔)
证明。 若要显示 P 表示旋转,请考虑下图。
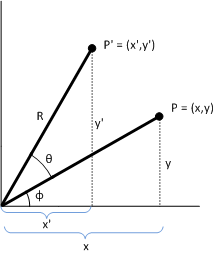
鉴于:
-
P = (x,y)
-
要转换的原始点。
-
Φ
-
由线条(0,0)到 P 构成的角度。
-
Θ
-
围绕原点旋转 (x,y) 的角度。
-
P' = (x',y')
-
转换的点。
-
R
-
行(0,0)到 P 的长度。此外,旋转圆的半径。
注意
此图使用几何图形中使用的标准坐标系,其中正 y 轴向上。 Direct2D 使用 Windows 坐标系,其中正 y 轴向下点。
x 轴和线条 (0,0) 到 P' 之间的角度为 Ф + Ф。 以下标识保留:
- x = R cosФ y = R sin^x' = R cos(Y' = R sin(Ф+ Ф)
现在,针对 2 的 x' 和 y' 进行求解。 按三角加法公式:
- x' = R(cosФcosФ – sinФsinФ) = RcosФcosФ – RsinФsinФ y' = R(sinФcosФ + cosФinФ) = RsinФcosФ + RcosФ
我们得到:
- x' = xcos≤ – ysin≤y' = xsin≤ + ycos≤
对应于前面所示的转换点 P。
围绕任意点旋转
若要围绕原点(x,y)旋转,请使用以下矩阵。
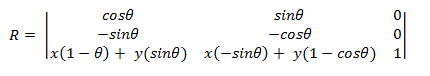
可以通过将点 (x,y) 取为原点来派生此矩阵。

让 (x1, y1) 成为旋转点 (x0, y0) 围绕点 (x,y) 产生的点(x,y)。 我们可以按如下所示派生 x1。
- x1 = (x0 – x)cos≤ (y0 – y)sin≤ + x x1 = x0cos≤ – y0sin≤ + \[ (1 – cos++) + ysin++ \]
现在,使用此公式 x1 = ax0 + cy0 + e 从前面插入转换矩阵。 使用相同的过程来派生 y1。
倾斜转换
倾斜转换由四个参数定义:
- :沿 x 轴倾斜的量,以 y 轴的角度测量。
- Ф:沿 y 轴倾斜的量,以 x 轴的角度测量。
- (px,py):执行倾斜的点的 x 坐标和 y 坐标。
倾斜转换使用以下矩阵。
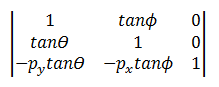
转换的点为:
- P' = (*x* + *y*tanФ – *py*tanФ, *y* + *x*tanФ) – *py*tanФ
或等效:
- P' = (*x* + (*y* – *py*)tanФ, *y* + (*x* – *px*)tanФ)
若要查看此转换的工作原理,请单独考虑每个组件。 射线参数将 x 方向上的每一个点都移入等于 tan^ 的量。 下图显示了 鲁斯与 x 轴倾斜之间的关系。

下面是应用于矩形的相同倾斜:

Ф 参数具有相同的效果,但沿 y 轴:
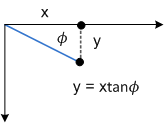
下图显示了应用于矩形的 y 轴倾斜。
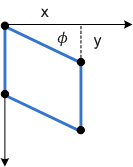
最后,参数 px,py 沿 x 轴和 y 轴移动偏斜的中心点。
表示 Direct2D 中的转换
所有 Direct2D 转换都是仿射转换。 Direct2D 不支持非仿射转换。 转换由 D2D1_MATRIX_3X2_F 结构表示。 此结构定义 3 × 2 矩阵。 由于相交转换的第三列始终相同([0,0,1]),并且由于 Direct2D 不支持非相交转换,因此无需指定整个 3 × 3 矩阵。 在内部,Direct2D 使用 3 个× 3 个矩阵来计算转换。
D2D1_MATRIX_3X2_F 的成员根据其索引位置命名:_11 成员是元素(1,1),_12 成员是元素(1,2),依此类推。 尽管可以直接初始化结构成员,但建议使用 D2D1::Matrix3x2F 类。 此类继承 D2D1_MATRIX_3X2_F,并提供用于创建任何基本相交转换的帮助程序方法。 该类还定义了用于组合两个或多个转换的 运算符*(),如在 Direct2D 中应用转换中所述。
下一个