参数曲线
媒体参数能够随时间推移跟随曲线。 每个曲线由一个数学公式和两个端点描述。 每个终点都由一个引用时间和该时间曲线的值定义。 公式用于计算点之间的中间值,并确定曲线的形状。 可能的曲线包括:
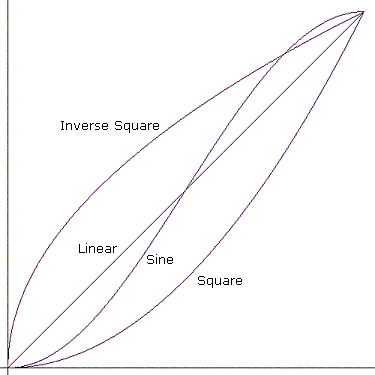
- 跳
- 线性
- Square
- 反正方形
- 正弦
“Jump”表示直接跳转到结束值。 下图显示了其他曲线。
从数学上看,曲线的工作方式如下。 假设曲线从时间 t₀ 开始,值为 v₀,在时间 t₁ 结束,值为 v₁。 定义曲线的两个点 (t₀、v₀) 和 (t₁ v₁) 。
- 让 Тt 为曲线的总持续时间, t₁–t₀。
- 让 Δv 是起始值和结束值 v₁–v₀ 之间的间隔。
- 在 t₀< = t<₁的任何时间,让 ーt' = t–t₀。
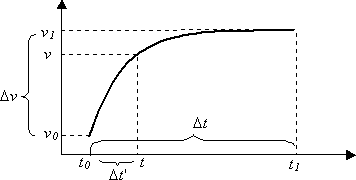
参数在 时间 t 的值为:
v = f ( Лt' / Тt ) * Лv + v₀
其中,f (x) 是由曲线类型确定的函数:
- 线性:y = x
- 正方形:y = x^2
- 反正方形:y = sqrt (x)
- 正弦值:y = [ sin (πx – π/2) + 1 ] / 2
请注意,Δt' <t,因此术语 Δt'/Δt 的范围从 0 到 1。 因此,f (x) 也介于 0 到 1 之间, v 始终介于 v₀ 和 v₁ 之间。 无论是 v₀ <v₁ 还是反之亦然,都是如此。 换句话说,曲线由 矩形 (t₀、 v₀、 t₁、 v₁) 绑定。
对于正弦曲线, (πx – π/2) 的值范围为 –π/2 到 π/2,这意味着 sin (πx – π/2) 范围为 –1 到 1。 然后规范化结果,使 f (x) (0-1) 范围。
相关主题