通过

在 Direct2D 中应用转换

  • 项目

在使用 Direct2D 绘图中，我们看到 ID2D1RenderTarget：：FillEllipse 方法绘制与 x 轴和 y 轴对齐的椭圆。 但是，假设你想绘制一个倾斜角度的椭圆吗？

显示倾斜椭圆的图像。

通过使用转换，可以通过以下方式更改形状。

  • 围绕点旋转。
  • 缩放。
  • 在 X 或 Y 方向) 平移 (位移。
  • 倾斜 (也称为 剪切) 。

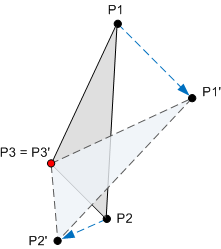
转换是将一组点映射到一组新点的数学运算。 例如，下图显示了围绕点 P3 旋转的三角形。 应用旋转后，点 P1 映射到 P1'，点 P2 映射到 P2'，点 P3 映射到自身。

显示围绕点旋转的关系图。

转换是使用矩阵实现的。 但是，无需了解矩阵的数学即可使用它们。 若要了解有关数学的详细信息，请参阅 附录：矩阵转换。

若要在 Direct2D 中应用转换，请调用 ID2D1RenderTarget：：SetTransform 方法。 此方法采用定义转换 的D2D1_MATRIX_3X2_F 结构。 可以通过调用 D2D1：：Matrix3x2F 类上的方法来初始化此结构。 此类包含为每种转换返回矩阵的静态方法：

例如，以下代码围绕点应用 20 度的旋转 (100， 100) 。

pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));

转换将应用于所有以后的绘制操作，直到再次调用 SetTransform 。 若要删除当前转换，请使用标识矩阵调用 SetTransform 。 若要创建标识矩阵，请调用 Matrix3x2F：：Identity 函数。

pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

绘制时钟手

让我们通过将 Circle 程序转换为模拟时钟来使用转换。 为此，我们可以为手添加线条。

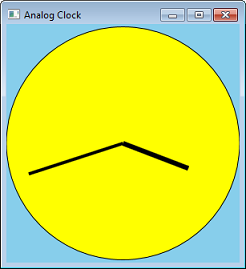
模拟时钟程序的屏幕截图。

我们可以计算角度，然后应用旋转转换，而不是计算线条的坐标。 下面的代码显示了一个绘制一个时钟手的函数。 fAngle 参数提供手的角度（以度为单位）。

void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
    m_pRenderTarget->SetTransform(
        D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
            );

    // endPoint defines one end of the hand.
    D2D_POINT_2F endPoint = D2D1::Point2F(
        m_ellipse.point.x,
        m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
        );

    // Draw a line from the center of the ellipse to endPoint.
    m_pRenderTarget->DrawLine(
        m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}

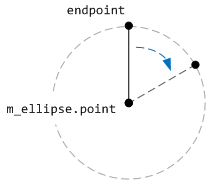
此代码绘制一条垂直线，从时钟面的中心开始，到 终点结束。 通过应用旋转转换，线条围绕椭圆的中心旋转。 旋转的中心点是形成时钟面的椭圆中心。

显示时钟手的旋转的关系图。

下面的代码演示如何绘制整个时钟面。

void Scene::RenderScene()
{
    m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));

    m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
    m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);

    // Draw hands
    SYSTEMTIME time;
    GetLocalTime(&time);

    // 60 minutes = 30 degrees, 1 minute = 0.5 degree
    const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
    const float fMinuteAngle =(360.0f / 60) * (time.wMinute);

    DrawClockHand(0.6f,  fHourAngle,   6);
    DrawClockHand(0.85f, fMinuteAngle, 4);

    // Restore the identity transformation.
    m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}

可以从 Direct2D 时钟示例下载完整的 Visual Studio 项目。 (为了好玩，下载版本向时钟面添加了径向)

组合转换

可以通过将两个或更多矩阵相乘来组合四个基本转换。 例如，以下代码将旋转与转换组合在一起。

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);

pRenderTarget->SetTransform(rot * trans);

Matrix3x2F 类为矩阵乘法提供运算符* () 。 矩阵相乘的顺序很重要。 将转换 (M × N) 意味着“先应用 M，然后应用 N”。例如，下面是旋转后跟转换：

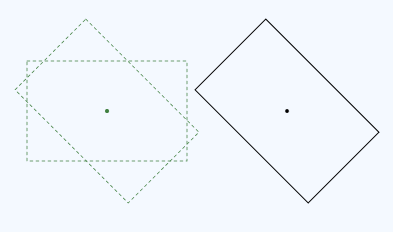
显示旋转后跟转换的关系图。

下面是此转换的代码：

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);

现在，将该转换与转换（按反向顺序、转换后旋转）进行比较。

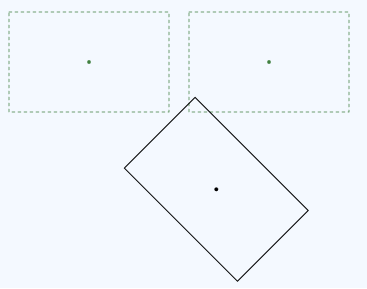
显示后跟旋转的转换的关系图。

围绕原始矩形的中心执行旋转。 下面是此转换的代码。

D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);

如你所看到的，矩阵是相同的，但操作顺序已更改。 发生这种情况是因为矩阵乘法不是可交换的：M × N ≠ N × M。

下一步

附录：矩阵转换