设备方位四元数矢量算法
本文介绍 Windows Hardware Lab Kit (Windows HLK) 使用的算法,该算法用于在高级方位传感器测试中确定 9 轴数据准确性的接收矢量和预期矢量之间的差异。 这些测试将验证传感器融合是否已正确集成,以及传感器融合所需的所有传感器是否都已正确集成和安装。
注意
在某些情况下,可以使用传感器诊断工具来检查接受测试的 3D 测斜仪和聚合设备方位传感器。
四元数矢量算法
该算法使用两个矢量的四维点积的 arc cos 除以两个矢量的大小乘积,然后再除以 2。 此算法如图 1 四元数矢量算法公式所示:
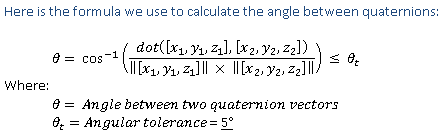
旋转矩阵值将转换为四元数值以进行精度验证。 计算所得的四元数矢量不应与预期的四元数向量偏离 +/- 5 度(与四元数矢量之间形成的角度相比的公差)(** 航向轴方向上允许 +/-10 度的精度)。 Windows HLK 测试允许 Øt 的差值最高达到 15 度。
如何计算接收的和预期的四元数矢量之间的增量角
本节介绍在 Windows HLK 的高级方位测试中,计算接收的四元数矢量和预期的四元数矢量之间的增量角的方法。
聚合设备方位传感器的数据报告中涉及以下两个数据值:
四元数矢量
旋转矩阵
测试包含以下两项验证:
验证传感器数据报告中接收到的四元数矢量。 四元数矢量的表示形式为 (xi + yj + zk + w)。
w 的值始终应为正值。
四元数矢量应规范化并且为非零。 例如,矢量的大小必须接近 1.0。 计算幅度时,提供百分之一 (1%) 的余地来弥补误差。
增量角是使用 delta = 2 * Acos( ( Exp . Rec ) / ( | Exp | * | Rec | ) ) 计算得出的,其中:
\* 指示标量乘法
. 指示点积
Exp 是预期的四元数矢量
Rec 是接收的四元数矢量
| Q | 指示四元数矢量的大小
增量是角度(以度为单位)
如果增量大于 360 度,则增量将通过以下方式重新计算:delta = delta - 360。
此时,增量应小于或等于容错值;例如,10度。
验证接收的旋转矩阵。 旋转矩阵应为 3x3 矩阵。
旋转矩阵的每个列和行矢量都必须规范化且为非零。 计算幅度时,提供百分之一 (1%) 的余地来弥补误差。
接收的旋转矩阵会转换为四元数矢量。
将重新使用验证 (1) 的从 <a> 到 <e> 的所有步骤。