评估不同类型的聚类分析
训练聚类分析模型
有多种算法可用于聚类分析。 最常使用的算法之一是 K-Means 聚类分析,其最简单的形式包括以下步骤:
- 对特征值进行向量化以定义 N 维坐标(其中 N 是特征数)。 在花的示例中,有两个特征:花瓣数和叶子数。 因此,特征向量具有两个坐标,可用于在二维空间中以概念形式绘制数据点。
- 决定要使用多少个群集来给花分组,并将此值称为 k。 例如,若要创建三个群集,则 k 值为 3。 然后,在随机坐标中绘制 k 点。 这些点将成为每个群集的中心点,因此它们被称为质心。
- 每个数据点(在本例中为一朵花)都被分配到最近的质心。
- 每个质心将根据分配给它的数据点之间的平均距离,移动到这些数据点的中心。
- 移动质心后,数据点现在可能更接近其他质心,因此数据点将根据新的最近的质心重新分配给群集。
- 质心移动和群集重新分配步骤会重复执行,直到群集变得稳定或达到预定的最大迭代次数为止。
下面的动画展示了此过程:

分层聚类分析
分层聚类分析是另一种类型的聚类分析算法,其中群集本身属于更大的组,而后者又属于更大的组,依此类推。 结果是,数据点可以是精度不同的群集:具有大量极小且精确的组,或少量却较大的组。
例如,如果将聚类分析应用于词的含义,则可能会获得一个组,其中包含特定于情感(“生气的”、“高兴的”等)的形容词。 该组所属的组包含所有和人类相关的形容词(“快乐”、“英俊”、“年轻”),而后者又属于更高级的组,其中包含所有形容词(“高兴”、“绿色”、“英俊”、“坚固”等)。
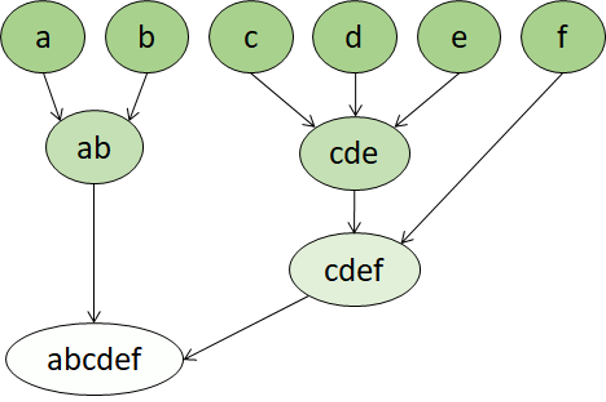
分层聚类不仅可用于将数据分组,还可用于了解这些组之间的关系。 分层聚类分析的主要优点是,它不需要提前定义群集数。 而且,此方法有时可以提供比非分层方法更具可解释性的结果。 主要缺点是,这些方法花费的计算时间可能比简单的方法更长,而且有时不适用于大型数据集。