什么是分类?
二元分类是包含两个类别的分类。 例如,我们可以将患者标记为非糖尿病患者或糖尿病患者。
通过以值的形式确定每个可能的类的概率来进行类预测,其中该值介于 0(不可能)到 1(确信)之间。 所有类别的总概率始终为 1,因为患者必定要么是患有糖尿病,要么是未患糖尿病。 因此,如果预测患者患糖尿病患者的概率为 0.3,那么患者为非糖尿病患者的对应概率为 0.7。
阈值(通常为 0.5)用于确定预测类。 如果正类(在本例中指患有糖尿病)的预测概率大于阈值,那么预测分类为患有糖尿病。
训练和评估分类模型
分类是受监督机器学习技术的示例,这意味着它依赖于包括已知特征值和已知标签值的数据。 在此示例中,特征值是患者的诊断度量值,标签值是非糖尿病或糖尿病的分类。 分类算法用于将数据的一部分拟合到函数中,该函数可根据特征值计算每个类标签的概率。 剩余数据用于将它根据特征生成的预测与已知类标签进行比较来评估模型。
一个简单示例
我们来看一个示例,它可帮助阐释关键原则。 假设我们有以下患者数据,其中包含一个特征(血糖水平)和一个类标签(0 表示未患糖尿病,1 表示患有糖尿病)。
| 血糖 | 糖尿病 |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
我们使用观察到的前 8 个值来训练分类模型,我们将先绘制出血糖特征 (x) 和预测的糖尿病标签 (y)。
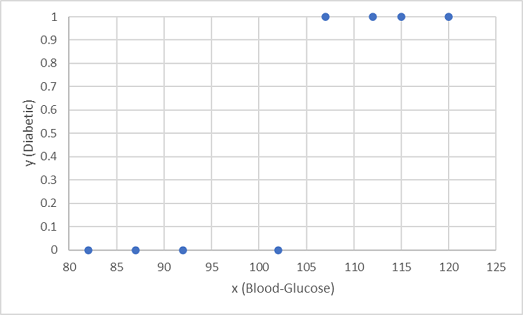
我们需要一个函数,用它来根据 x 计算 y 的概率值(换句话说,我们需要函数 f(x) = y)。 从图表中可以看到,血糖水平低的患者全都未患糖尿病,而血糖水平更高的患者患有糖尿病。 似乎血糖水平越高,患者患有糖尿病的概率就越大,拐点在 100 到 110 之间的某个位置。 我们需要拟合一个函数,计算 y 轴介于 0 到 1 的某个值来得到这些值。
logistic函数就是这样的一个函数,它得出 S 形曲线。
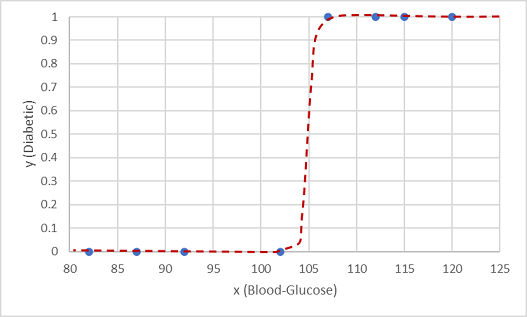
现在,我们可使用该函数,查找 x 的函数行上的点来根据 x 的任意值计算 y 为阳性(表示患者患有糖尿病)的概率值。 我们可将阈值设置为 0.5 作为类标签预测的分界点。
让我们用保留的两个数据值测试一下。
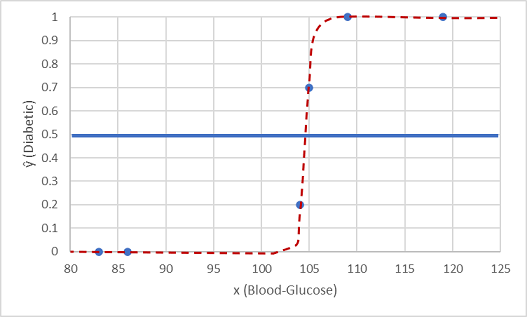
在阈值线下方绘制的点将生成预测类 0(未患糖尿病),在该线上方的点将被预测为 1(患有糖尿病)。
现在,我们可根据模型中封装的逻辑函数,将标签预测结果(ŷ或 "y-hat")与实际的类标签 (y) 进行比较。
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |