量子计算中的叠加是什么?
如果上一单元中的猫是量子猫,那么量子猫和盒子系统的状态不会改变:量子猫在盒子中的六个不同位置的总和,按在某位置找到量子猫的概率加权。 唯一的区别是,传统猫只能位于六个可能位置中的一个(且仅有一个),而量子猫可以同时处于所有六个位置上!
在传统世界中,物体一次只能处于一种状态。 但是在量子世界中,量子粒子可以同时处于多个状态。 这种现象称为叠加。
可惜的是,在量子计算中,我们不使用量子猫,而是量子比特。 “qubit”是“quantum bit”的缩写,中文意思是“量子比特”。 传统计算中的基本信息单位是比特,而在量子计算中,基本信息单元是量子比特。 就像位可以采用两个可能的值 0 和 1 一样,量子比特是可以处于两个可能状态的任何量子粒子。 例如,量子比特可以是光子,它可以在两个方向上极化,也可以是电子,它可以处于两个能级。
如何表示量子比特中的叠加? 找到某一特定状态量子比特的概率是多少?
如何表示量子比特中的叠加?
量子比特是具有两个可能位置或状态的量子粒子。 与传统比特类似,量子比特的量子态也称为 $0$ 和 $1$。 一个量子比特可以处于 $0$ 状态、$1$ 状态,以及这两种状态的任意叠加态。 如何表示这种叠加?
假设你画一个圆,并以圆心为坐标原点画一条横轴和一条纵轴。 将状态 $0$ 置于纵轴的上交点,将状态 $1$ 置于下交点。
如何描述这种表示形式? 你可以说,状态 $0$ 是指向上方的箭头或矢量,而状态 $1$ 是指向下方的矢量。 因此,经典比特是指向上方或下方的矢量,但永远不会指向另一种方向。
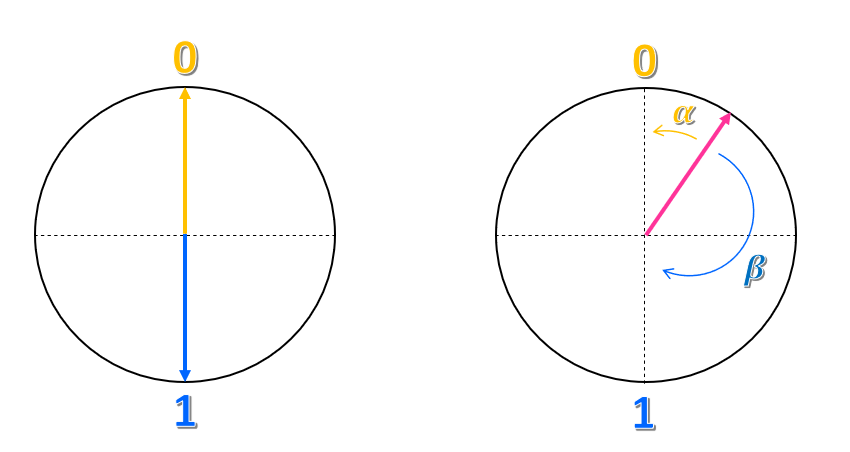
圆上其他的点又表示什么呢? 如何表示相应的状态? 与平面中的坐标一样,你可以尝试将状态表示为 $0$ 和 $1$ 两种状态的组合。 例如,可以取矢量与状态 $0$ 的接近程度,并将该角度称为 $\alpha$;取矢量与状态 $1$ 的接近程度,并将该角度称为 $\beta$。 我们可以将状态表示为 $\alpha 0 + \beta 1 $。 因此,该状态是状态 $0$ 和 $1$ 的叠加。
就像箱中猫的示例一样,量子比特的全局状态是各个状态($0$ 和 $1$)的总和,并按照找到处于该状态($\alpha$ 和 $\beta$)的量子比特的概率加权。
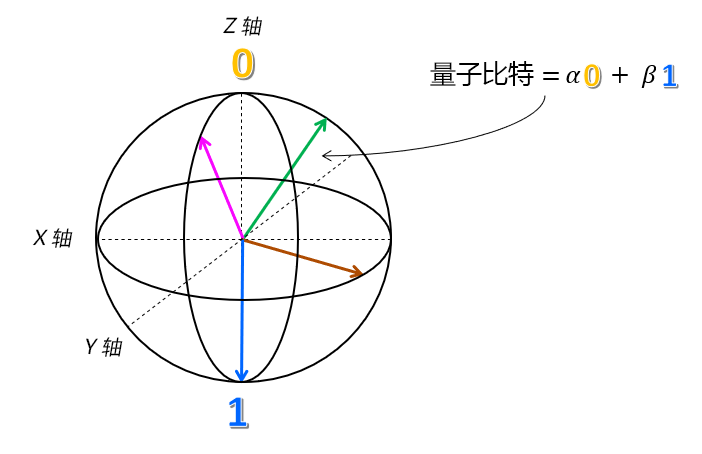
量子比特的这种表示形式实际上是准确的,它称为布洛赫球。
提示
布洛赫球是一个强大的工具,因为可以针对量子比特执行的操作可以表示为围绕其中一个基本轴的旋转。 虽然将量子计算视为一系列旋转是一种强大的直觉,但是使用这种直觉来设计和描述算法非常困难。 Q# 通过提供一种描述此类旋转的语言来缓解此问题。
找到处于某种状态的量子比特的概率是多少?
与上一单元的猫和盒子的示例一样,量子比特的整体状态是各个状态的总和,$0$ 和 $1$,其权重是找到某状态量子比特的概率,即 $\alpha$ 和 $\beta $。 数字 $\alpha$ 和 $\beta$ 分别表示量子比特状态与状态 $0$ 和 $1$ 的“接近程度”。 那么,$\alpha$ 和 $\beta$ 是找到处于 $0$ 或 $1$ 状态的量子比特的概率吗? 不完全是。
数字 $\alpha$ 和 $\beta$ 是每种状态的概率幅度。 它们的绝对值(例如 $|\alpha|^2$)提供相应的概率。 例如,观测到状态 $0$ 的概率为 $|\alpha|^2$,观测到状态 $1$ 的概率为 $|\beta|^2$。
数字 $\alpha$ 和 $\beta$ 可以是正数、负数甚至复数。 但是,在有效的量子叠加中,所有概率的总和必须为 1:$|\alpha|^2+|\beta|^2=1$。 此约束称为规范化条件。 可以将标准化条件看作这样一个事实,即在测量时总是得到一个结果,因此测量每个可能结果的概率之和必须为 1。