如何使用纠缠来发送信息？

7 分钟

在前面的单元中，你了解到量子纠缠可以是量子通信的优秀资源。在本单元中，你将看到纠缠最有名的应用之一：量子隐形传态协议。

在隐形传态中，纠缠用于将量子比特的状态从一个位置传输到另一个位置。量子比特的状态将传输到另一个量子比特，但量子比特本身不会以物理方式移动。这是记住的一个重要事项！量子比特状态的信息将传输到另一个量子比特，该量子比特用作容器以写入消息量子比特的信息。

隐形传态协议使用纠缠和经典通信的组合。传统通信非常重要，因为传送协议要求发送方将其度量结果传达给接收方。这意味着隐形传态不能发送比光速更快的信息。发送方和接收方之间的经典通信受光速的限制。

让我们回顾一下量子传出协议。

量子传送协议

Alice 和 Bob 在同一家公司合作。 Alice 总部设在西雅图，Bob 位于洛杉矶。他们正在处理需要他们共享量子信息的项目。他们决定使用量子传送在它们之间发送量子信息。

初始设置

Alice 和 Bob 各自都有一个量子位，该量子位是以前准备的纠缠对的一部分。纠缠对是贝尔状态，这是状态

$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$

Alice 具有一个名为“消息量子比特”的额外量子比特，并希望将此量子比特发送到 Bob。消息量子比特处于 Alice 希望传送到 Bob 的未知状态。消息量子比特的状态为

$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m，$$

其中 $\alpha$ 和 $\beta$ 为复数。

Alice 和 Bob 三个量子比特的全局状态为

$$\ket{\text{全局}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$

图中显示了一个女人和一个代表 Alice 和 Bob 的男人的两张脸表情符号。Alice 拥有两个量子比特，其中一个与 Bob 的量子位纠缠在一起。纠缠量子比特的颜色相同，表示它们正在纠缠。消息量子比特是不同的颜色。

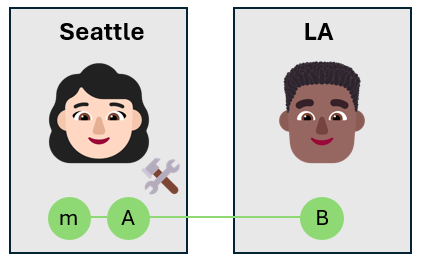
Alice 将消息量子比特与她自己的量子比特纠缠在一起

Alice 采用消息量子比特，并使用 CNOT 门将它与自己的量子比特 $A$ 纠缠在一起。消息量子比特是控制量子比特，Alice 的量子比特是 target 量子比特。这会创建三量子位纠缠状态。

图中显示了一个女人的两张脸表情符号和一个代表 Alice 和 Bob 的男人，以及一个代表 Alice 操纵其量子位的锤子表情符号。这三个量子比特的颜色相同，表示它们纠缠在一起。

消息量子比特处于未知状态 $\alpha\ket{0}_m + \beta\ket{1}_m$，因此在应用 CNOT 门后，Alice 的量子比特位于四个 Bell 状态的叠加中。三个量子比特的全局状态为

$$\ket{\text{全局}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$

$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$

$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$

$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$

Alice 和 Bob 量子比特的全局状态是四种可能状态的叠加。

提示

一个很好的练习是验证三个量子比特的全局状态是否为上面给出的状态。为此，可以将 CNOT 门应用到消息量子比特和 Alice 的量子比特，然后扩展三个量子比特的状态。

Alice 测量量子比特

然后 Alice 测量消息量子比特和她自己的量子比特。她不会像往常一样测量 $Z$ 基的量子比特，而是选择贝尔基数。 Bell 基础包括四个 Bell 状态：$\lbrace \ket{\phi^+}、\ket{\phi^-}、\ket{\psi^+}、\ket{\psi^-} \rbrace$。

通过测量 Bell 基数的消息量子比特和她自己的量子比特，Alice 将她的量子比特投影到四个 Bell 状态之一。由于三个量子比特纠缠，因此度量结果是相关的。当 Alice 测量她的量子比特时，Bob 的量子比特也投影到相关状态。

例如，如果 Alice 测量她的量子比特并观察状态 $\ket{\phi^-}$，则 Bob 的量子比特投影到状态 $\alpha\ket{0}_B - \beta\ket{1}_B$。

图中显示了一个女人的两张脸表情符号和一个代表 Alice 和 Bob 的男人，以及一个代表 Alice 操纵其量子位的锤子表情符号。Alice 的量子比特是相同的颜色，表示它们纠缠，而 Bob 的量子比特是不同的颜色。

Alice 调用 Bob

爱丽丝打电话给鲍勃，告诉他她的测量结果。她使用经典通信渠道，如电话呼叫或短信。

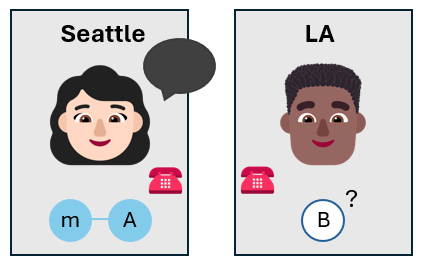
显示一个女人的两张脸表情符号和一个代表 Alice 和 Bob 的男人，以及一个代表 Alice 呼叫 Bob 的电话表情符号。

鲍勃现在知道自己的量子比特的状态，而无需测量它。 Bob 量子比特的状态可能与 Alice 想要传送的消息量子比特的状态不同，但很接近。

Bob 应用量子操作

接下来，Bob 可以通过向量子比特应用特定的量子运算来恢复消息量子比特的原始状态。鲍勃的行动取决于爱丽丝通过电话告诉他什么。

显示一个女人和一个代表爱丽丝和鲍勃的两张脸表情符号的关系图。Bob 将操作应用于他的量子比特，由锤子表情符号表示。Bob 的量子比特与消息量子比特的颜色相同。

他执行的操作可以是 Pauli $X$ 门，Pauli $Z$ 门，或两者都没有。

例如，如果 Alice 的度量结果为 $\ket{\phi^-}$，Bob 知道他的量子比特处于状态 $(\alpha\ket{0}_B - \beta\ket{1}_B)。$ 他只需要应用 Pauli Z 门来恢复消息量子比特的原始状态。

Alice 度量值	Bob 应用
$\ket{\phi^+}$	无操作
$\ket{\phi^-}$	Pauli Z 门
$\ket{\psi^+}$	Pauli X 门
$\ket{\psi^-}$	Pauli X 门后跟 Pauli Z 门

此最终操作有效地将消息量子比特的状态传送到 Bob 的量子比特。任务完成！

重要

将操作应用于量子位与测量它不同。当 Bob 应用操作时，他不会测量他的量子比特。他应用一个量子运算来更改量子比特的状态，但不折叠它。