绘制弧线的三个方法
了解如何使用 SkiaSharp 以三种不同的方式定义弧线
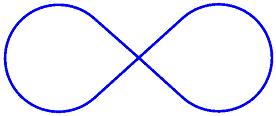
弧是椭圆形的周长上的曲线,例如此无穷大符号的圆弧部分:
尽管该定义很简单,但无法定义一个满足所有需求的弧绘制函数,因此在图形系统中并没有关于最佳绘制弧线方式的共识。因此,SKPath 类不会仅限于一种方法。
SKPath 定义一种 AddArc 方法、五种不同的 ArcTo 方法和两个相对的 RArcTo 方法。 这些方法分为三类,表示三种指定弧线的截然不同的方法。你使用哪一个取决于可用于定义弧线的信息,以及此弧线如何与要绘制的其他图形相适应。
角弧
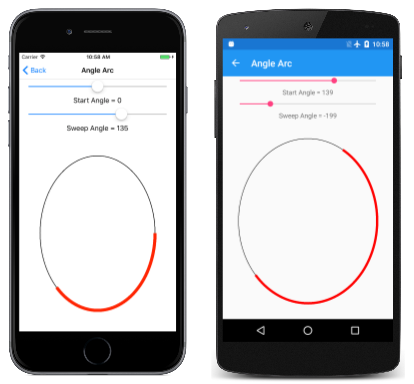
用角弧法绘制弧线时,需要指定一个矩形来包围椭圆形。 此椭圆形圆周上的弧线由椭圆形中心的角度表示,这些角度表示弧线的起点和长度。 有两种不同的方法来绘制角弧。 以下是 AddArc 方法和 ArcTo 方法:
public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)
public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)
这些方法与 Android AddArc 和 [ArcTo]xref:Android.Graphics.Path.ArcTo*) 方法相同。 iOS AddArc 方法是相似的,但仅限于圆周上的弧线,而不是推广到椭圆形。
这两种方法都以定义椭圆形的位置和大小的 SKRect 值开头:
弧是这个椭圆形的周长的一部分。
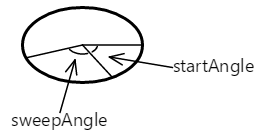
startAngle 参数是相对于从椭圆形中心向右绘制的水平线的顺时针角度,以度为单位。 sweepAngle 参数相对于 startAngle。 下面是分别为 60 度和 100 度的 startAngle 和 sweepAngle 值:
弧线从起始角度开始。 其长度由扫描角度控制。 弧线在此处以红色显示:
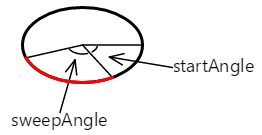
使用 AddArc 或 ArcTo 方法添加到路径的曲线只是椭圆形周长的一部分:

startAngle 或 sweepAngle 参数可以是负值:弧线在正值 sweepAngle 时为顺时针方向,在负值 时为反时针方向。
但是,AddArc不会定义封闭轮廓。 如果在 AddArc 后调用 LineTo,则在 LineTo 法中,从弧的末端到点画一条直线,在 ArcTo 法中也是如此。
AddArc 会自动启动新的轮廓线,在功能上等效于使用具有最终参数的 true 调用 ArcTo:
path.ArcTo (oval, startAngle, sweepAngle, true);
最后一个参数称为 forceMoveTo,它实际上会导致在弧线开头的 MoveTo 调用。这会开始新的轮廓。 false 的最后一个参数并非如此:
path.ArcTo (oval, startAngle, sweepAngle, false);
此版本的 ArcTo 会从当前位置绘制到弧线的开头。这意味着弧线可以位于较大轮廓中间的某个位置。
“角弧线”页允许使用两个滑块来指定起始角度和扫描角度。 XAML 文件会实例化两个 Slider 元素和一个 SKCanvasView。 AngleArcPage.xaml.cs 文件中的 PaintCanvas 处理程序使用定义为字段的两个 SKPaint 对象绘制椭圆和弧线:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
float startAngle = (float)startAngleSlider.Value;
float sweepAngle = (float)sweepAngleSlider.Value;
canvas.DrawOval(rect, outlinePaint);
using (SKPath path = new SKPath())
{
path.AddArc(rect, startAngle, sweepAngle);
canvas.DrawPath(path, arcPaint);
}
}
如你所见,起始角度和扫描角度都可以采用负值:
生成弧线的方法在算法上是最简单的方法,并且很容易派生描述弧线的参数公式。知道椭圆形的大小和位置,以及起始角和扫描角,就可以用简单的三角法计算出弧线的起点和终点:
x = oval.MidX + (oval.Width / 2) * cos(angle)
y = oval.MidY + (oval.Height / 2) * sin(angle)
该 angle 值为或 startAngle 或 startAngle + sweepAngle。
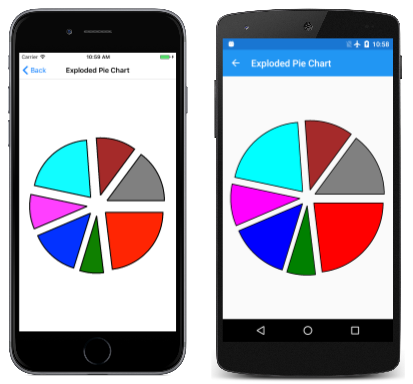
使用两个角度来定义弧线最适合知道要绘制的弧线的角长度的情况,例如,要绘制饼图。 “分解饼图”页对此进行了演示。 ExplodedPieChartPage 类使用内部类来定义一些捏造的数据和颜色:
class ChartData
{
public ChartData(int value, SKColor color)
{
Value = value;
Color = color;
}
public int Value { private set; get; }
public SKColor Color { private set; get; }
}
ChartData[] chartData =
{
new ChartData(45, SKColors.Red),
new ChartData(13, SKColors.Green),
new ChartData(27, SKColors.Blue),
new ChartData(19, SKColors.Magenta),
new ChartData(40, SKColors.Cyan),
new ChartData(22, SKColors.Brown),
new ChartData(29, SKColors.Gray)
};
PaintSurface 处理程序首先会循环访问项以计算 totalValues 数字。 从中可以确定每个项的大小作为总计的分数,并将其转换为角度:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
int totalValues = 0;
foreach (ChartData item in chartData)
{
totalValues += item.Value;
}
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float explodeOffset = 50;
float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
SKRect rect = new SKRect(center.X - radius, center.Y - radius,
center.X + radius, center.Y + radius);
float startAngle = 0;
foreach (ChartData item in chartData)
{
float sweepAngle = 360f * item.Value / totalValues;
using (SKPath path = new SKPath())
using (SKPaint fillPaint = new SKPaint())
using (SKPaint outlinePaint = new SKPaint())
{
path.MoveTo(center);
path.ArcTo(rect, startAngle, sweepAngle, false);
path.Close();
fillPaint.Style = SKPaintStyle.Fill;
fillPaint.Color = item.Color;
outlinePaint.Style = SKPaintStyle.Stroke;
outlinePaint.StrokeWidth = 5;
outlinePaint.Color = SKColors.Black;
// Calculate "explode" transform
float angle = startAngle + 0.5f * sweepAngle;
float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);
canvas.Save();
canvas.Translate(x, y);
// Fill and stroke the path
canvas.DrawPath(path, fillPaint);
canvas.DrawPath(path, outlinePaint);
canvas.Restore();
}
startAngle += sweepAngle;
}
}
为每个饼图切片以创建新的 SKPath 对象。 该路径由中间的一条线组成,然后是绘制弧线的 ArcTo,另一条线时从 Close 调用返回的中心结果。 此程序通过将“分解”饼片从中心移出 50 像素来显示“分解”饼片。 该项任务需要每个切片的扫描角度中点方向上的一个矢量:
若要查看没有“分解”的外观,只需注释禁止 Translate 调用:
切线弧
SKPath 支持的第二种类型的弧是 切线弧,之所以称为相切弧,是因为弧是与两条相连直线相切的圆的周长。
将正切弧添加到具有两个 SKPoint 参数的 ArcTo 方法的路径,或具有点的单独 Single 参数的 ArcTo 重载:
public void ArcTo (SKPoint point1, SKPoint point2, Single radius)
public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)
此 ArcTo 方法类似于 PostScript arct(第 532 页)函数和 iOS AddArcToPoint 方法。
ArcTo 方法涉及三点:
- 轮廓的当前点;如果未调用
MoveTo,则为点 (0, 0) ArcTo方法的第一个点参数,称为角点ArcTo方法的第二个点参数,称为目标点:

这三个点定义两条连接线:
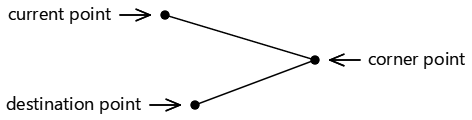
如果这三个点共线,即它们位于同一条直线上,将不会绘制任何弧。
ArcTo 方法还包括 radius 参数。 这将定义圆的半径:

切弧并不能概括为椭圆形。
如果两条线以任意角度相交,那么可以在这些线之间插入一个圆,使其与两条线都相切:
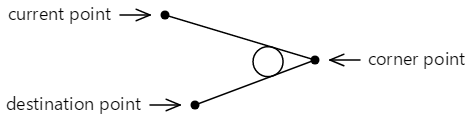
在轮廓上添加的曲线不会触碰到 ArcTo 方法中指定的任何一个点。 它包括一条从当前点到第一个切点的直线,以及一条以第二个切点为终点的弧线,此处以红色显示:
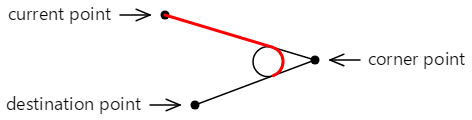
这是添加到轮廓的最终直线和弧线:

轮廓可以从第二个切点继续。
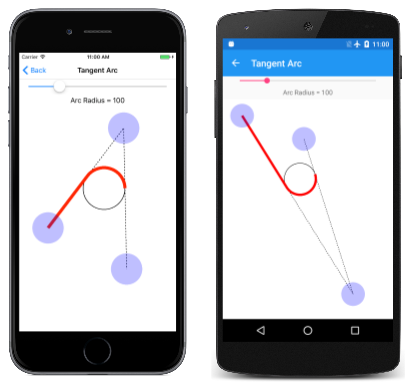
切线弧页面允许尝试使用切线弧。这是派生自 InteractivePage 的多个页面中的第一个页面,它定义了一些方便的 SKPaint 对象并会执行 TouchPoint 处理:
public class InteractivePage : ContentPage
{
protected SKCanvasView baseCanvasView;
protected TouchPoint[] touchPoints;
protected SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
StrokeWidth = 3
};
protected SKPaint redStrokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 15
};
protected SKPaint dottedStrokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
StrokeWidth = 3,
PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
};
protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
baseCanvasView.InvalidateSurface();
}
}
}
TangentArcPage 类从 InteractivePage 派生。 TangentArcPage.xaml.cs 文件中的构造函数负责实例化和初始化 touchPoints 数组,并将 baseCanvasView(在 InteractivePage 中)设置为 TangentArcPage.xaml 文件中实例化的 SKCanvasView 对象:
public partial class TangentArcPage : InteractivePage
{
public TangentArcPage()
{
touchPoints = new TouchPoint[3];
for (int i = 0; i < 3; i++)
{
TouchPoint touchPoint = new TouchPoint
{
Center = new SKPoint(i == 0 ? 100 : 500,
i != 2 ? 100 : 500)
};
touchPoints[i] = touchPoint;
}
InitializeComponent();
baseCanvasView = canvasView;
radiusSlider.Value = 100;
}
void sliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
PaintSurface 处理程序使用 ArcTo 方法基于触摸点和 Slider 绘制弧线,同时也以算法方式计算角度所基于的圆:
public partial class TangentArcPage : InteractivePage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw the two lines that meet at an angle
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.LineTo(touchPoints[1].Center);
path.LineTo(touchPoints[2].Center);
canvas.DrawPath(path, dottedStrokePaint);
}
// Draw the circle that the arc wraps around
float radius = (float)radiusSlider.Value;
SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);
double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
double angleBetween = Math.Acos(dotProduct);
float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
touchPoints[1].Center.Y + vMid.Y * hypotenuse);
canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);
// Draw the tangent arc
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
canvas.DrawPath(path, redStrokePaint);
}
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
}
下面是正在运行的切线弧页面:
切线弧是创建圆角的理想选择,比如圆角矩形。 由于 SKPath 已包含 AddRoundedRect 方法,所以圆角七边形页面展示了如何使用 ArcTo 来使七边形的角变圆。 (对于任何常规多边形,代码已通用化。)
RoundedHeptagonPage 类的 PaintSurface 处理程序包含一个 for 循环,用于计算七个顶点的坐标,并通过这些顶点计算出七条边的中点。 然后,这些中点用于构造路径:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
float cornerRadius = 100;
int numVertices = 7;
float radius = 0.45f * Math.Min(info.Width, info.Height);
SKPoint[] vertices = new SKPoint[numVertices];
SKPoint[] midPoints = new SKPoint[numVertices];
double vertexAngle = -0.5f * Math.PI; // straight up
// Coordinates of the vertices of the polygon
for (int vertex = 0; vertex < numVertices; vertex++)
{
vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
radius * (float)Math.Sin(vertexAngle));
vertexAngle += 2 * Math.PI / numVertices;
}
// Coordinates of the midpoints of the sides connecting the vertices
for (int vertex = 0; vertex < numVertices; vertex++)
{
int prevVertex = (vertex + numVertices - 1) % numVertices;
midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
(vertices[prevVertex].Y + vertices[vertex].Y) / 2);
}
// Create the path
using (SKPath path = new SKPath())
{
// Begin at the first midpoint
path.MoveTo(midPoints[0]);
for (int vertex = 0; vertex < numVertices; vertex++)
{
SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];
// Draws a line from the current point, and then the arc
path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);
// Connect the arc with the next midpoint
path.LineTo(nextMidPoint);
}
path.Close();
// Render the path in the center of the screen
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 10;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.DrawPath(path, paint);
}
}
}
下面是正在运行的程序:
椭圆弧
椭圆弧被添加到路径中,该路径调用具有两个 SKPoint 参数的 ArcTo 方法,或具有单独的 X 和 Y 坐标的 ArcTo 重载:
public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)
public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)
椭圆弧与可缩放矢量图形 (SVG) 和通用 Windows 平台 ArcSegment 类中包含的椭圆弧 一致。
这些 ArcTo 方法在两个点之间,即轮廓的当前点和 ArcTo 方法的最后一个参数(xy 参数或单独的 x 和 y 参数)之间绘制弧线:

ArcTo 方法(r,或 rx 和 ry)的第一个点参数根本不是点,而是指定椭圆形的水平和垂直弧度;
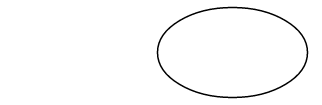
xAxisRotate 参数是旋转此椭圆形的顺时针度数:

如果将此倾斜椭圆形定位,使其与该两点相交,那么这两个点就会被两条不同的弧线连接起来:
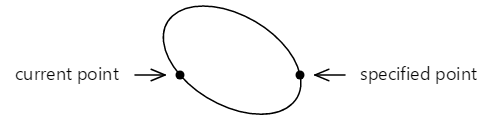
这两个弧可以通过两种方式区分开来:顶部的弧比底部的弧大,并且当从左到右绘制弧时,顶部的弧是顺时针方向绘制的,而底部的弧是逆时针方向绘制的。
还可以以另一种方式将两个点之间的椭圆形拟合:
现在,上面有一个顺时针绘制的较小弧线,下面有一个逆时针绘制的较大弧线。
因此,这两个点可以由倾斜椭圆形定义的弧线连接,共有四种方式:

这四条弧线由 ArcTo 方法的 SKPathArcSize 和 SKPathDirection 枚举类型参数的四种组合区分开来:
- 红色:SKPathArcSize.Large 和 SKPathDirection.Clockwise
- 绿色:SKPathArcSize.Small 和 SKPathDirection.Clockwise
- 蓝色: SKPathArcSize.Small 和 SKPathDirection.CounterClockwise
- 品红色:SKPathArcSize.Large 和 SKPathDirection.CounterClockwise
如果倾斜椭圆不够大,不适合两个点之间的大小,则会将其均匀缩放,直到足够大。 在这种情况下,只有两条唯一的弧连接这两个点。 可以使用 SKPathDirection 参数来进行区分。
虽然这种定义弧线的方法乍听之下很复杂,但它是唯一一种可以用旋转椭圆形定义弧线的方法,而且在需要将弧线与轮廓的其他部分整合时,它往往是最简单的方法。
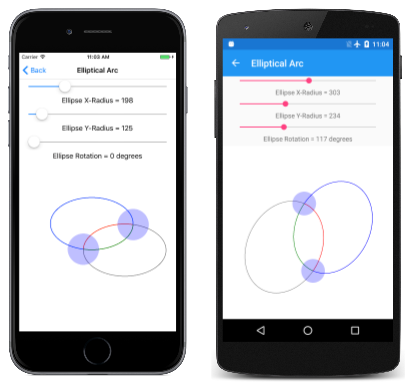
椭圆形弧页允许以交互方式设置两个点,以及椭圆形的大小和旋转角度。 EllipticalArcPage 类派生自 InteractivePage,EllipticalArcPage.xaml.cs 代码隐藏文件中的 PaintSurface 处理程序会绘制四个弧:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
int colorIndex = 0;
SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
(float)yRadiusSlider.Value);
float rotation = (float)rotationSlider.Value;
foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
{
path.MoveTo(touchPoints[0].Center);
path.ArcTo(ellipseSize, rotation,
arcSize, direction,
touchPoints[1].Center);
strokePaint.Color = colors[colorIndex++];
canvas.DrawPath(path, strokePaint);
path.Reset();
}
}
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
此处它正在运行:
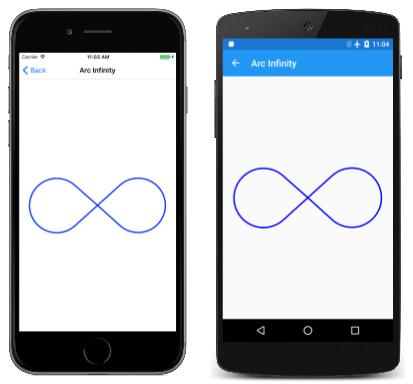
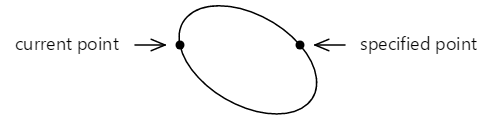
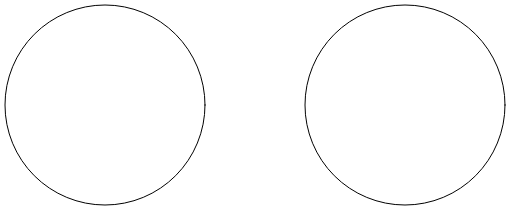
弧无穷大页面使用椭圆弧绘制无穷大符号。 无穷大符号的基础是两个半径为 100 个单位的圆,中间相隔 100 个单位:
相交的两条直线分别与两个圆相切:
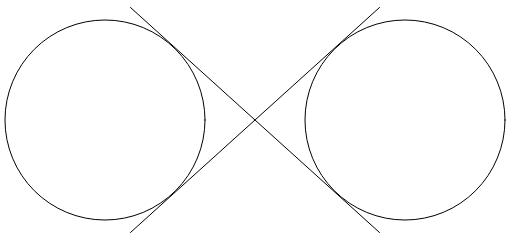
无限符号由这些圆的部分和两条线组合而成。 要使用椭圆弧绘制无穷大符号,必须确定两条直线与圆相切的坐标。
在其中一个圆中构造一个直角矩形:
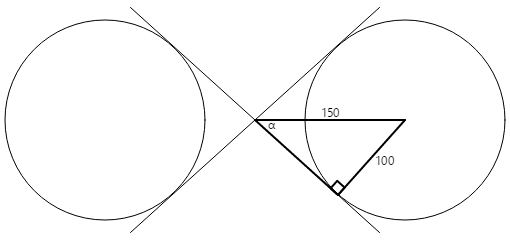
圆的半径是 100 个单位,三角形的斜边是 150 个单位,因此角度 α 是 100 除以 150 的余弦(反正弦),即 41.8 度。 三角形的另一边长是 41.8 度的余弦值乘以 150,即 112,也可以通过勾股定理计算得出。
然后,可以使用以下信息计算切点的坐标:
x = 112·cos(41.8) = 83
y = 112·sin(41.8) = 75
只需四个切点,就能绘制出以点 (0, 0) 为中心、圆半径为 100 的无穷大符号:
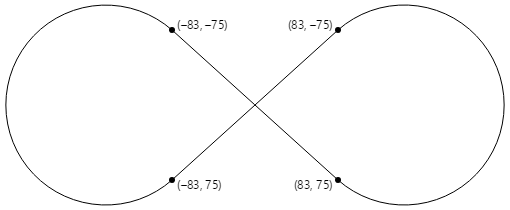
ArcInfinityPage 类中的 PaintSurface 处理程序将无穷大符号定位在页面中心,使 (0, 0) 点位于页面中心,并根据屏幕尺寸缩放路径:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.LineTo(83, 75);
path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
path.LineTo(-83, 75);
path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
path.Close();
// Use path.TightBounds for coordinates without control points
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
该代码使用 SKPath 的 Bounds 属性来确定无穷大正弦的尺寸,以将其缩放为画布的大小:
结果似乎有点小,这表明 SKPath 的 Bounds 属性报告的大小大于路径。
在内部,Skia 使用多条二次贝塞尔曲线逼近弧线。 这些曲线(在下一节中将会看到)包含控制点,这些控制点控制曲线的绘制方式,但并不是渲染曲线的一部分。 该 Bounds 属性包括这些控制点。
若要获得更紧密的拟合度,请使用排除控制点的 TightBounds 属性。 下面是在横向模式下运行的程序,并使用 TightBounds 属性获取路径边界:
虽然弧线和直线之间的连接在数学上是平滑的,但从弧线到直线的改变似乎有点突然。 下一篇文章“贝塞尔曲线的三种类型”将介绍更好的无穷大符号。