System.Drawing.Drawing2D.Matrix 类

本文提供了此 API 参考文档的补充说明。

该 Matrix 类封装表示几何转换的 3 by-3 仿射矩阵。

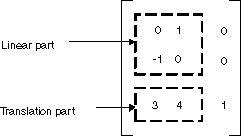
在 GDI+中，可以将相交转换存储在对象中 Matrix 。 因为表示仿射变换的矩阵的第三列始终为 (0, 0, 1)，所以在构造 Matrix 对象时仅指定前两列中的六个数字。 该语句 Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) 构造下图所示的矩阵。

注意

在 .NET 6 及更高版本中， 仅 Windows 操作系统支持包含此类型的 System.Drawing.Common 包。 在跨平台应用中使用此类型会导致编译时警告和运行时异常。 有关详细信息，请参阅 仅在 Windows 上支持的 System.Drawing.Common。

复合转换

复合变换是一个接一个的一系列变换。 考虑以下列表中的矩阵和变换：

Matrix	转换
矩阵 A	旋转 90 度
矩阵 B	在 x 方向上缩放 2 倍
矩阵 C	在 y 方向平移 3 个单位

如果从点 （2， 1） 开始 - 由矩阵 [2 1 1] 表示， 乘以 A， 然后 B， 然后 C， 点 （2， 1） 将按列出的顺序进行三个转换。

[2 1 1]ABC = [-2 5 1]

与其将复合变换的三个部分存储在三个单独的矩阵中，不如将 A、B 和 C 相乘以得到一个 3×3 矩阵来存储整个复合变换。 假设 ABC = D。 然后，乘以 D 的点将得到与 A 乘以 A、B、C 相同的结果。

[2 1 1]D = [-2 5 1]

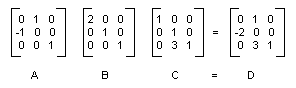
下图显示了矩阵 A、B、C 和 D。

复合变换的矩阵可以通过乘以单个变换矩阵来形成，这一事实意味着任何顺序的仿射变换都可以存储在单个 Matrix 对象中。

注意

复合变换的顺序很重要。 一般来说，旋转、缩放、平移与缩放、旋转、平移是不同的。 同样，矩阵乘法的顺序也很重要。 一般来说，ABC 与 BAC 不同。

Matrix 类提供了几种构建复合变换的方法：Multiply、Rotate、RotateAt、Scale、Shear 和 Translate。 以下示例创建复合变换矩阵，该矩阵首先旋转 30 度，然后在 y 方向上缩放 2 倍，然后在 x 方向上平移 5 个单位：

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)