演练：矩阵乘法

本分步演练演示如何使用 C++ AMP 加速矩阵乘法的执行。 提供了两种算法，一种不使用平铺，一种使用平铺。

先决条件

开始之前：

• 阅读 C++ AMP 概述。
• 阅读使用平铺。
• 确保至少运行 Windows 7 或 Windows Server 2008 R2。

注意

从 Visual Studio 2022 版本 17.0 开始，已弃用 C++ AMP 标头。 包含任何 AMP 标头都会导致生成错误。 应在包含任何 AMP 标头之前定义 _SILENCE_AMP_DEPRECATION_WARNINGS，以使警告静音。

创建项目

创建新项目的说明因安装的 Visual Studio 版本而异。 若要查看 Visual Studio 首选项的文档，请使用“版本”选择器控件。 它位于此页面上目录表的顶部。

在 Visual Studio 中创建项目

1. 在菜单栏上，选择“文件”>“新建”>“项目”，打开“创建新项目”对话框 。

2. 在对话框顶部，将“语言”设置为“C++”，将“平台”设置为“Windows”，并将“项目类型”设置为“控制台”。

3. 从筛选的项目类型列表中，选择“空项目”，然后选择“下一步”。 在下一页中的“名称”框内输入“MatrixMultiply”以指定项目的名称，并根据需要指定项目位置。

   

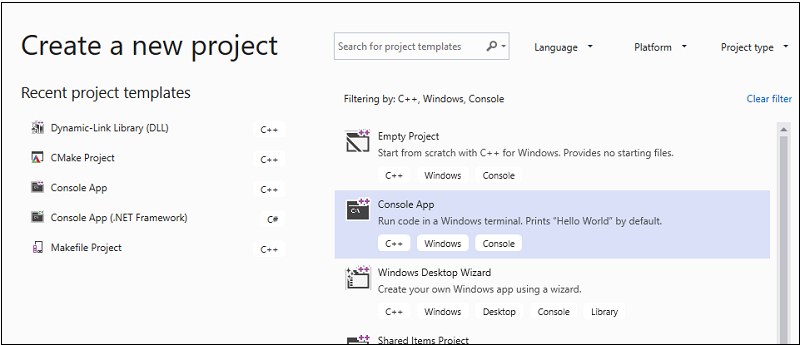
4. 选择“创建”按钮创建客户端项目。

5. 在“解决方案资源管理器”中，打开“源文件”的快捷菜单，然后选择“添加”>“新项”。

6. 在“添加新项”对话框中，选择“C++ 文件(.cpp)”，在“名称”框中输入“MatrixMultiply.cpp”，然后选择“添加”按钮。

不使用平铺的乘法

在本部分中，请考虑两个矩阵（A 和 B）的乘法，定义如下：

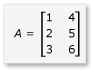
A 是 3x2 矩阵，B 是 2x3 矩阵。 A 和 B 的乘积是以下 3x3 矩阵。 乘积通过逐个元素将 A 的行乘以 B 的列进行计算。

在不使用 C++ AMP 的情况下相乘

1. 打开 MatrixMultiply.cpp，并使用以下代码替换现有代码。

   #include <iostream>
   
   void MultiplyWithOutAMP() {
       int aMatrix[3][2] = {{1, 4}, {2, 5}, {3, 6}};
       int bMatrix[2][3] = {{7, 8, 9}, {10, 11, 12}};
       int product[3][3] = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}};
   
       for (int row = 0; row < 3; row++) {
           for (int col = 0; col < 3; col++) {
               // Multiply the row of A by the column of B to get the row, column of product.
               for (int inner = 0; inner < 2; inner++) {
                   product[row][col] += aMatrix[row][inner] * bMatrix[inner][col];
               }
               std::cout << product[row][col] << "  ";
           }
           std::cout << "\n";
       }
   }
   
   int main() {
       MultiplyWithOutAMP();
       getchar();
   }
   

   该算法是矩阵乘法定义的简单实现。 它不使用任何并行或线程算法来减少计算时间。

2. 在菜单栏上，依次选择“文件”>“全部保存”。

3. 选择 F5 键盘快捷方式以开始调试并验证输出是否正确。

4. 选择 Enter 以退出应用程序。

使用 C++ AMP 相乘

1. 在 MatrixMultiply.cpp 中，在 main 方法之前添加以下代码。

   void MultiplyWithAMP() {
   int aMatrix[] = { 1, 4, 2, 5, 3, 6 };
   int bMatrix[] = { 7, 8, 9, 10, 11, 12 };
   int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 };
   
   array_view<int, 2> a(3, 2, aMatrix);
   
   array_view<int, 2> b(2, 3, bMatrix);
   
   array_view<int, 2> product(3, 3, productMatrix);
   
   parallel_for_each(product.extent,
      [=] (index<2> idx) restrict(amp) {
          int row = idx[0];
          int col = idx[1];
          for (int inner = 0; inner <2; inner++) {
              product[idx] += a(row, inner)* b(inner, col);
          }
      });
   
   product.synchronize();
   
   for (int row = 0; row <3; row++) {
      for (int col = 0; col <3; col++) {
          //std::cout << productMatrix[row*3 + col] << "  ";
          std::cout << product(row, col) << "  ";
      }
      std::cout << "\n";
     }
   }
   

   AMP 代码类似于非 AMP 代码。 对 parallel_for_each 的调用为 product.extent 中的每个元素启动一个线程，并替换行和列的 for 循环。 idx 中提供了行和列的单元格的值。 可以使用 [] 运算符和索引变量，或者 () 运算符和行列变量来访问 array_view 对象的元素。 示例演示两种方法。 array_view::synchronize 方法将 product 变量的值复制回 productMatrix 变量。

2. 在 MatrixMultiply.cpp 的顶部添加以下 include 和 using 语句。

   #include <amp.h>
   using namespace concurrency;
   

3. 修改 main 方法以调用 MultiplyWithAMP 方法。

   int main() {
       MultiplyWithOutAMP();
       MultiplyWithAMP();
       getchar();
   }
   

4. 按 Ctrl+F5 键盘快捷方式，以开始调试并验证输出是否正确。

5. 按空格键以退出应用程序。

使用平铺的乘法

平铺是一种将数据分区成大小相等的子集（称为平铺）的技术。 使用平铺时会有三个改变。

• 可以创建 tile_static 变量。 访问 tile_static 空间中的数据可能比访问全局空间中的数据要快得多。 为每个平铺创建 tile_static 变量的实例，平铺中的所有线程可以访问该变量。 平铺的主要好处是可以从 tile_static 访问中获得性能增益。

• 可以调用 tile_barrier::wait 方法，以在指定代码行的一个平铺中停止所有线程。 不能保证线程的运行顺序，只有一个平铺中的所有线程都在调用 tile_barrier::wait 时停止，才能继续执行。

• 可以访问相对于整个 array_view 对象的索引以及相对于平铺的索引。 使用局部索引可使代码更易于阅读和调试。

若要利用矩阵乘法中的平铺，算法必须将矩阵分区成平铺，然后将平铺数据复制到 tile_static 变量中以加快访问速度。 在此示例中，矩阵分区成大小相等的子矩阵。 乘积通过将子矩阵相乘而得出。 此示例中的两个矩阵及其乘积为：

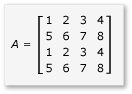
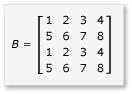
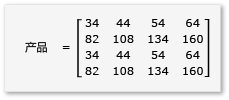
矩阵分区成四个 2x2 矩阵，定义如下：

现在可以按以下方式撰写和计算 A 和 B 的乘积：

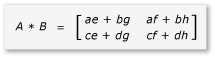
由于矩阵 a 到 h 是 2x2 矩阵，因此其所有乘积及和也是 2x2 矩阵。 它还遵循 A 和 B 的乘积是 4x4 矩阵，与预期一样。 若要快速检查算法，请计算乘积中第一行与第一列相交处的元素的值。 在此示例中，这将是 ae + bg 的第一行与第一列相交处的元素的值。 只需计算每个术语的 ae 和 bg 的第一列与第一行。 ae 的值为 (1 * 1) + (2 * 5) = 11。 (3 * 1) + (4 * 5) = 23 的值为 bg。 最终值是正确的 11 + 23 = 34。

若要实现此算法，代码：

• 在 parallel_for_each 调用中使用 tiled_extent 对象，而不是 extent 对象。

• 在 parallel_for_each 调用中使用 tiled_index 对象，而不是 index 对象。

• 创建 tile_static 变量以保留子矩阵。

• 使用 tile_barrier::wait 方法停止线程以计算子矩阵的乘积。

使用 AMP 和平铺相乘

1. 在 MatrixMultiply.cpp 中，在 main 方法之前添加以下代码。

   void MultiplyWithTiling() {
       // The tile size is 2.
       static const int TS = 2;
   
       // The raw data.
       int aMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 };
       int bMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 };
       int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
   
       // Create the array_view objects.
       array_view<int, 2> a(4, 4, aMatrix);
       array_view<int, 2> b(4, 4, bMatrix);
       array_view<int, 2> product(4, 4, productMatrix);
   
       // Call parallel_for_each by using 2x2 tiles.
       parallel_for_each(product.extent.tile<TS, TS>(),
           [=] (tiled_index<TS, TS> t_idx) restrict(amp)
           {
               // Get the location of the thread relative to the tile (row, col)
               // and the entire array_view (rowGlobal, colGlobal).
               int row = t_idx.local[0];
               int col = t_idx.local[1];
               int rowGlobal = t_idx.global[0];
               int colGlobal = t_idx.global[1];
               int sum = 0;
   
               // Given a 4x4 matrix and a 2x2 tile size, this loop executes twice for each thread.
               // For the first tile and the first loop, it copies a into locA and e into locB.
               // For the first tile and the second loop, it copies b into locA and g into locB.
               for (int i = 0; i < 4; i += TS) {
                   tile_static int locA[TS][TS];
                   tile_static int locB[TS][TS];
                   locA[row][col] = a(rowGlobal, col + i);
                   locB[row][col] = b(row + i, colGlobal);
                   // The threads in the tile all wait here until locA and locB are filled.
                   t_idx.barrier.wait();
   
                   // Return the product for the thread. The sum is retained across
                   // both iterations of the loop, in effect adding the two products
                   // together, for example, a*e.
                   for (int k = 0; k < TS; k++) {
                       sum += locA[row][k] * locB[k][col];
                   }
   
                   // All threads must wait until the sums are calculated. If any threads
                   // moved ahead, the values in locA and locB would change.
                   t_idx.barrier.wait();
                   // Now go on to the next iteration of the loop.
               }
   
               // After both iterations of the loop, copy the sum to the product variable by using the global location.
               product[t_idx.global] = sum;
           });
   
       // Copy the contents of product back to the productMatrix variable.
       product.synchronize();
   
       for (int row = 0; row <4; row++) {
           for (int col = 0; col <4; col++) {
               // The results are available from both the product and productMatrix variables.
               //std::cout << productMatrix[row*3 + col] << "  ";
               std::cout << product(row, col) << "  ";
           }
           std::cout << "\n";
       }
   }
   

   此示例明显不同于不使用平铺的示例。 代码使用以下概念步骤：

   1. 将 a 的平铺[0,0] 的元素复制到 locA 中。 将 b 的平铺[0,0] 的元素复制到 locB 中。 请注意，product 是平铺的，而不是 a 和 b。 因此，使用全局索引访问 a, b 和 product。 调用 tile_barrier::wait 至关重要。 它会停止平铺中的所有线程，直到填充完 locA 和 locB。

   2. 将 locA 与 locB 相乘并将结果放入 product 中。

   3. 将 a 的 tile[0,1] 的元素复制到 locA 中。 将 b 的 tile[1,0] 的元素复制到 locB 中。

   4. 将 locA 与 locB 相乘并将它们添加到已在 product 中的结果。

   5. tile[0,0] 的乘法已完成。

   6. 对其他四个平铺重复上述步骤。 没有专门为平铺编制索引，线程可以按任意顺序执行。 执行每个线程时，会相应地为每个平铺创建 tile_static 变量，并且对 tile_barrier::wait 的调用控制程序流。

   7. 仔细检查算法时，请注意，每个子矩阵都加载到 tile_static 内存中两次。 数据传输确实需要一段时间。 但是，一旦数据位于 tile_static 内存中，对数据的访问速度要快得多。 由于计算乘积需要重复访问子矩阵中的值，因此总体性能提升。 对于每种算法，需要试验才能找到最佳算法和平铺大小。

   在非 AMP 和非平铺示例中，从全局内存访问 A 和 B 的每个元素四次，以计算乘积。 在平铺示例中，每个元素从全局内存访问两次，并从 tile_static 内存访问四次。 这不是显著的性能提升。 但是，如果 A 和 B 是 1024x1024 矩阵，平铺大小为 16，则性能将显著提升。 在这种情况下，每个元素将仅复制到 tile_static 内存中 16 次，并从 tile_static 内存访问 1024 次。

2. 如下所示修改 main 方法以调用 MultiplyWithTiling 方法。

   int main() {
       MultiplyWithOutAMP();
       MultiplyWithAMP();
       MultiplyWithTiling();
       getchar();
   }
   

3. 按 Ctrl+F5 键盘快捷方式，以开始调试并验证输出是否正确。

4. 按空格键以退出应用程序。

另请参阅

C++ AMP (C++ Accelerated Massive Parallelism)
演练：调试 C++ AMP 应用程序