你当前正在访问 Microsoft Azure Global Edition 技术文档网站。如果需要访问由世纪互联运营的 Microsoft Azure 中国技术文档网站，请访问 https://docs.azure.cn。

运行资源估算器的不同方式

项目
10/16/2024

本文介绍如何使用 Azure Quantum 资源估算器。资源估算器是 Quantum 开发工具包的一部分，可在不同的平台和 IDE 中使用。

如果运行 Q# 程序，则资源估算器可在 Visual Studio Code 中使用 Quantum 开发工具包扩展。无需拥有 Azure 订阅即可在 Visual Studio Code 中使用资源估算器。

如果运行 Qiskit 或 QIR 程序，资源估算器可在Azure 门户中使用，并且需要 Azure 订阅才能使用它。

下表显示了运行资源估算器的不同方法。

用户方案	平台	教程
估计 Q# 程序的资源	Visual Studio Code	在页面顶部的 VS Code 中选择 Q#
估计 Q# 计划的资源（高级）	Visual Studio Code 中的 Jupyter Notebook	在页面顶部的 Jupyter Notebook 中选择 Q#
估计 Qiskit 计划的资源	Azure 门户	在页面顶部Azure 门户中选择 Qiskit
估计 QIR 计划的资源	Azure 门户	提交 QIR
使用 FCIDUMP 文件作为参数参数（高级）	Visual Studio Code	提交量子化学问题

VS Code 的先决条件

最新版本的 Visual Studio Code 或打开网页版 VS Code。
最新版本的 Azure Quantum 开发工具包扩展。有关安装详细信息，请参阅在 VS Code 上安装 QDK。

提示

无需有 Azure 帐户即可运行本地资源估算器。

创建新的 Q# 文件

打开 Visual Studio Code 并选择“文件”>“新建文本文件”以创建新文件。
将文件另存为 ShorRE.qs。此文件将包含程序的 Q# 代码。

创建量子算法

将以下代码复制到 ShorRE.qs 文件中：


    import Std.Arrays.*;
    import Std.Canon.*;
    import Std.Convert.*;
    import Std.Diagnostics.*;
    import Std.Math.*;
    import Std.Measurement.*;
    import Microsoft.Quantum.Unstable.Arithmetic.*;
    import Std.ResourceEstimation.*;

    operation Main() : Unit {
        let bitsize = 31;

        // When choosing parameters for `EstimateFrequency`, make sure that
        // generator and modules are not co-prime
        let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
    }

    // In this sample we concentrate on costing the `EstimateFrequency`
    // operation, which is the core quantum operation in Shors algorithm, and
    // we omit the classical pre- and post-processing.

    /// # Summary
    /// Estimates the frequency of a generator
    /// in the residue ring Z mod `modulus`.
    ///
    /// # Input
    /// ## generator
    /// The unsigned integer multiplicative order (period)
    /// of which is being estimated. Must be co-prime to `modulus`.
    /// ## modulus
    /// The modulus which defines the residue ring Z mod `modulus`
    /// in which the multiplicative order of `generator` is being estimated.
    /// ## bitsize
    /// Number of bits needed to represent the modulus.
    ///
    /// # Output
    /// The numerator k of dyadic fraction k/2^bitsPrecision
    /// approximating s/r.
    operation EstimateFrequency(
        generator : Int,
        modulus : Int,
        bitsize : Int
    )
    : Int {
        mutable frequencyEstimate = 0;
        let bitsPrecision =  2 * bitsize + 1;

        // Allocate qubits for the superposition of eigenstates of
        // the oracle that is used in period finding.
        use eigenstateRegister = Qubit[bitsize];

        // Initialize eigenstateRegister to 1, which is a superposition of
        // the eigenstates we are estimating the phases of.
        // We first interpret the register as encoding an unsigned integer
        // in little endian encoding.
        ApplyXorInPlace(1, eigenstateRegister);
        let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);

        // Use phase estimation with a semiclassical Fourier transform to
        // estimate the frequency.
        use c = Qubit();
        for idx in bitsPrecision - 1..-1..0 {
            within {
                H(c);
            } apply {
                // `BeginEstimateCaching` and `EndEstimateCaching` are the operations
                // exposed by Azure Quantum Resource Estimator. These will instruct
                // resource counting such that the if-block will be executed
                // only once, its resources will be cached, and appended in
                // every other iteration.
                if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
                    Controlled oracle([c], (1 <<< idx, eigenstateRegister));
                    EndEstimateCaching();
                }
                R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
            }
            if MResetZ(c) == One {
                set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
            }
        }

        // Return all the qubits used for oracles eigenstate back to 0 state
        // using Microsoft.Quantum.Intrinsic.ResetAll.
        ResetAll(eigenstateRegister);

        return frequencyEstimate;
    }

    /// # Summary
    /// Interprets `target` as encoding unsigned little-endian integer k
    /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
    /// p is `power`, g is `generator` and N is `modulus`.
    ///
    /// # Input
    /// ## generator
    /// The unsigned integer multiplicative order ( period )
    /// of which is being estimated. Must be co-prime to `modulus`.
    /// ## modulus
    /// The modulus which defines the residue ring Z mod `modulus`
    /// in which the multiplicative order of `generator` is being estimated.
    /// ## power
    /// Power of `generator` by which `target` is multiplied.
    /// ## target
    /// Register interpreted as little endian encoded which is multiplied by
    /// given power of the generator. The multiplication is performed modulo
    /// `modulus`.
    internal operation ApplyOrderFindingOracle(
        generator : Int, modulus : Int, power : Int, target : Qubit[]
    )
    : Unit
    is Adj + Ctl {
        // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
        // also use `ExpModI` to compute a by which x must be multiplied. Also
        // note that we interpret target as unsigned integer in little-endian
        // encoding.
        ModularMultiplyByConstant(modulus,
                                    ExpModI(generator, power, modulus),
                                    target);
    }

    /// # Summary
    /// Performs modular in-place multiplication by a classical constant.
    ///
    /// # Description
    /// Given the classical constants `c` and `modulus`, and an input
    /// quantum register  |𝑦⟩, this operation
    /// computes `(c*x) % modulus` into |𝑦⟩.
    ///
    /// # Input
    /// ## modulus
    /// Modulus to use for modular multiplication
    /// ## c
    /// Constant by which to multiply |𝑦⟩
    /// ## y
    /// Quantum register of target
    internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
    : Unit is Adj + Ctl {
        use qs = Qubit[Length(y)];
        for (idx, yq) in Enumerated(y) {
            let shiftedC = (c <<< idx) % modulus;
            Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
        }
        ApplyToEachCA(SWAP, Zipped(y, qs));
        let invC = InverseModI(c, modulus);
        for (idx, yq) in Enumerated(y) {
            let shiftedC = (invC <<< idx) % modulus;
            Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
        }
    }

    /// # Summary
    /// Performs modular in-place addition of a classical constant into a
    /// quantum register.
    ///
    /// # Description
    /// Given the classical constants `c` and `modulus`, and an input
    /// quantum register  |𝑦⟩, this operation
    /// computes `(x+c) % modulus` into |𝑦⟩.
    ///
    /// # Input
    /// ## modulus
    /// Modulus to use for modular addition
    /// ## c
    /// Constant to add to |𝑦⟩
    /// ## y
    /// Quantum register of target
    internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
    : Unit is Adj + Ctl {
        body (...) {
            Controlled ModularAddConstant([], (modulus, c, y));
        }
        controlled (ctrls, ...) {
            // We apply a custom strategy to control this operation instead of
            // letting the compiler create the controlled variant for us in which
            // the `Controlled` functor would be distributed over each operation
            // in the body.
            //
            // Here we can use some scratch memory to save ensure that at most one
            // control qubit is used for costly operations such as `AddConstant`
            // and `CompareGreaterThenOrEqualConstant`.
            if Length(ctrls) >= 2 {
                use control = Qubit();
                within {
                    Controlled X(ctrls, control);
                } apply {
                    Controlled ModularAddConstant([control], (modulus, c, y));
                }
            } else {
                use carry = Qubit();
                Controlled AddConstant(ctrls, (c, y + [carry]));
                Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
                Controlled AddConstant([carry], (modulus, y));
                Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
            }
        }
    }

    /// # Summary
    /// Performs in-place addition of a constant into a quantum register.
    ///
    /// # Description
    /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
    /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
    ///
    /// # Input
    /// ## c
    /// Constant number to add to |𝑦⟩.
    /// ## y
    /// Quantum register of second summand and target; must not be empty.
    internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
        // We are using this version instead of the library version that is based
        // on Fourier angles to show an advantage of sparse simulation in this sample.

        let n = Length(y);
        Fact(n > 0, "Bit width must be at least 1");

        Fact(c >= 0, "constant must not be negative");
        Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");

        if c != 0 {
            // If c has j trailing zeroes than the j least significant bits
            // of y won't be affected by the addition and can therefore be
            // ignored by applying the addition only to the other qubits and
            // shifting c accordingly.
            let j = NTrailingZeroes(c);
            use x = Qubit[n - j];
            within {
                ApplyXorInPlace(c >>> j, x);
            } apply {
                IncByLE(x, y[j...]);
            }
        }
    }

    /// # Summary
    /// Performs greater-than-or-equals comparison to a constant.
    ///
    /// # Description
    /// Toggles output qubit `target` if and only if input register `x`
    /// is greater than or equal to `c`.
    ///
    /// # Input
    /// ## c
    /// Constant value for comparison.
    /// ## x
    /// Quantum register to compare against.
    /// ## target
    /// Target qubit for comparison result.
    ///
    /// # Reference
    /// This construction is described in [Lemma 3, arXiv:2201.10200]
    internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
    : Unit is Adj+Ctl {
        let bitWidth = Length(x);

        if c == 0 {
            X(target);
        } elif c >= 2 ^ bitWidth {
            // do nothing
        } elif c == 2 ^ (bitWidth - 1) {
            ApplyLowTCNOT(Tail(x), target);
        } else {
            // normalize constant
            let l = NTrailingZeroes(c);

            let cNormalized = c >>> l;
            let xNormalized = x[l...];
            let bitWidthNormalized = Length(xNormalized);
            let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));

            use qs = Qubit[bitWidthNormalized - 1];
            let cs1 = [Head(xNormalized)] + Most(qs);
            let cs2 = Rest(xNormalized);

            within {
                for i in IndexRange(gates) {
                    (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
                }
            } apply {
                ApplyLowTCNOT(Tail(qs), target);
            }
        }
    }

    /// # Summary
    /// Internal operation used in the implementation of GreaterThanOrEqualConstant.
    internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
        within {
            ApplyToEachA(X, [control1, control2]);
        } apply {
            ApplyAnd(control1, control2, target);
            X(target);
        }
    }

    internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
    : Unit is Adj {
        body (...) {
            CCNOT(control1, control2, target);
        }
        adjoint (...) {
            H(target);
            if (M(target) == One) {
                X(target);
                CZ(control1, control2);
            }
        }
    }


    /// # Summary
    /// Returns the number of trailing zeroes of a number
    ///
    /// ## Example
    /// ```qsharp
    /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
    /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
    /// ```
    internal function NTrailingZeroes(number : Int) : Int {
        mutable nZeroes = 0;
        mutable copy = number;
        while (copy % 2 == 0) {
            set nZeroes += 1;
            set copy /= 2;
        }
        return nZeroes;
    }

    /// # Summary
    /// An implementation for `CNOT` that when controlled using a single control uses
    /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
    internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
        body (...) {
            CNOT(a, b);
        }

        adjoint self;

        controlled (ctls, ...) {
            // In this application this operation is used in a way that
            // it is controlled by at most one qubit.
            Fact(Length(ctls) <= 1, "At most one control line allowed");

            if IsEmpty(ctls) {
                CNOT(a, b);
            } else {
                use q = Qubit();
                within {
                    ApplyAnd(Head(ctls), a, q);
                } apply {
                    CNOT(q, b);
                }
            }
        }

        controlled adjoint self;
    }

运行资源估算器

资源估算器提供六个预定义的量子比特参数，其中四个具有基于入口的指令集，两个具有 Majorana 指令集。它还提供两个量子错误代码， surface_code 以及 floquet_code。

此示例中使用 qubit_gate_us_e3 量子比特参数和 surface_code 量子纠错代码运行资源估算器。

选择 “视图 -> 命令面板”，然后键入“resource”，应显示 Q#：计算资源估算 选项。还可以单击操作前Main显示的命令列表中的“估计”。选择此选项可打开“资源估算器”窗口。
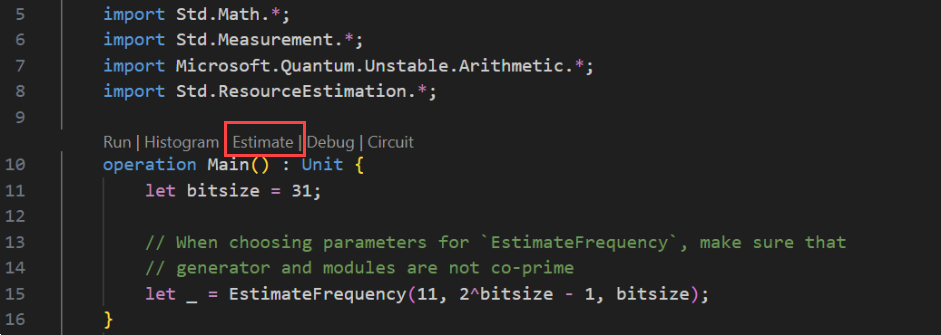
可以选择一个或多个“量子比特参数 + 纠错代码”类型来估算其资源。对于此示例，选择“qubit_gate_us_e3”，然后单击“确定”。
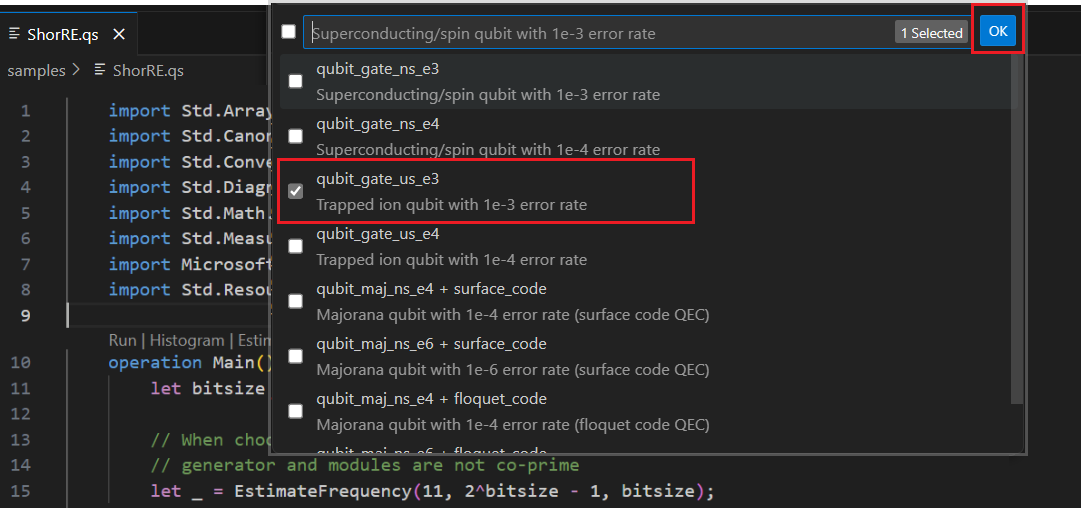
指定“错误预算”或接受默认值 0.001。对于此示例，请保留默认值，然后按 Enter。
按 Enter 接受基于文件名的默认结果名称，在本例中为 ShorRE。

查看结果

资源估算器为同一算法提供了多个估计值，每个算法都显示了量子比特数与运行时之间的权衡。了解运行时和系统规模之间的权衡是资源估算的更重要方面之一。

资源估算的结果显示在“Q# 估算”窗口中。

“结果”选项卡显示资源估算的摘要。单击第一行旁边的图标，选择要显示的列。可以从运行名称、估计类型、量子比特类型、qec 方案、错误预算、逻辑量子比特、逻辑深度、代码距离、T 状态、T 工厂、T 工厂、T 工厂分数、运行时、rQOPS 和物理量子比特中进行选择。

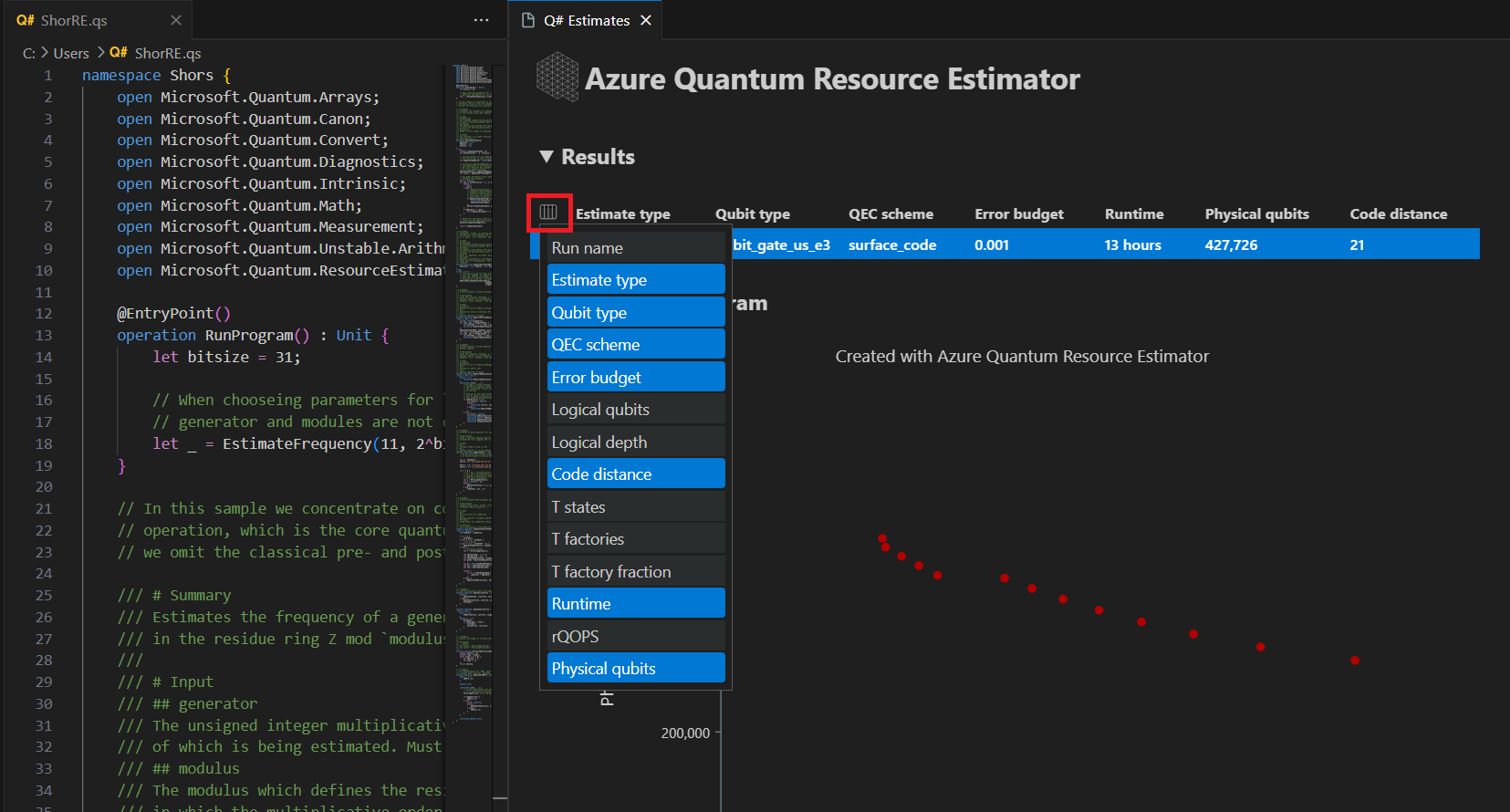
在结果表的“估计类型”列中，可以看到算法的 {量子比特数，运行时} 的最佳组合数。可以在时空图中查看这些组合。
空间图显示了物理量子比特数与算法运行时之间的权衡。在这种情况下，资源估算器发现 13 种不同的最佳组合数千个可能的组合。可以将鼠标悬停在每个 {数量的量子比特，运行时} 点上以查看该点的资源估算的详细信息。

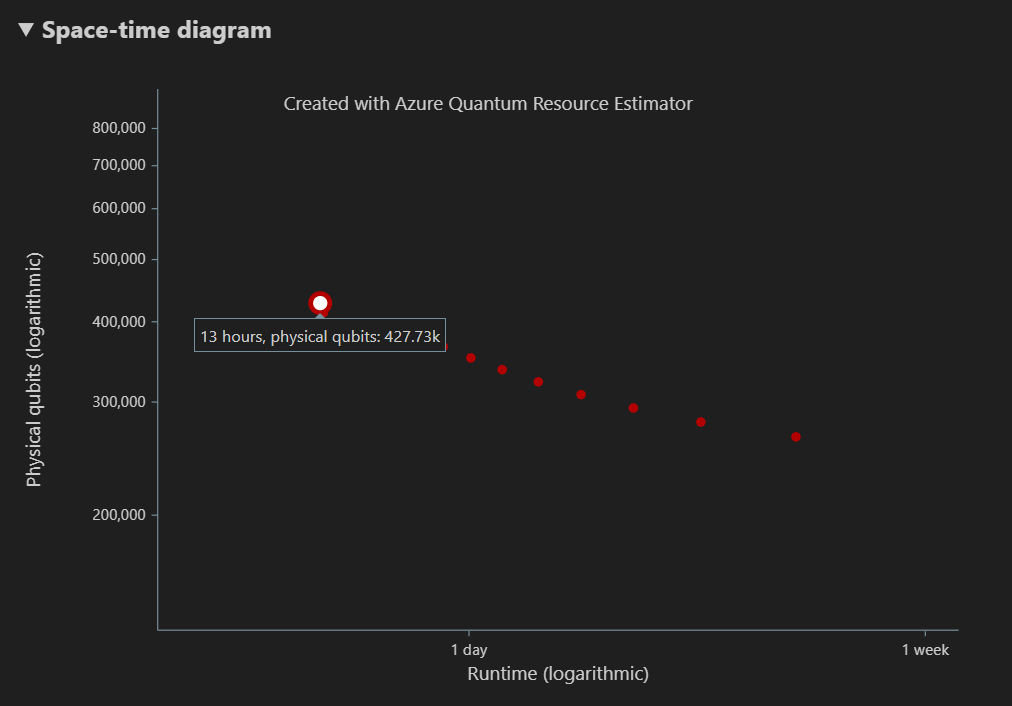
有关详细信息，请参阅时空图。

注意

你需要 单击一个空间时间点 ，即 {数量的量子比特，运行时} 对，以查看空间关系图以及对应于该点的资源估算的详细信息。
空间图显示了用于算法的物理量子比特和 T 工厂的分布，对应于 {数量的量子比特，运行时} 对。例如，如果在空间图中选择最左边的点，则运行算法所需的物理量子比特数427726，其中196686算法量子比特，其中 231040 个是 T 工厂量子比特。

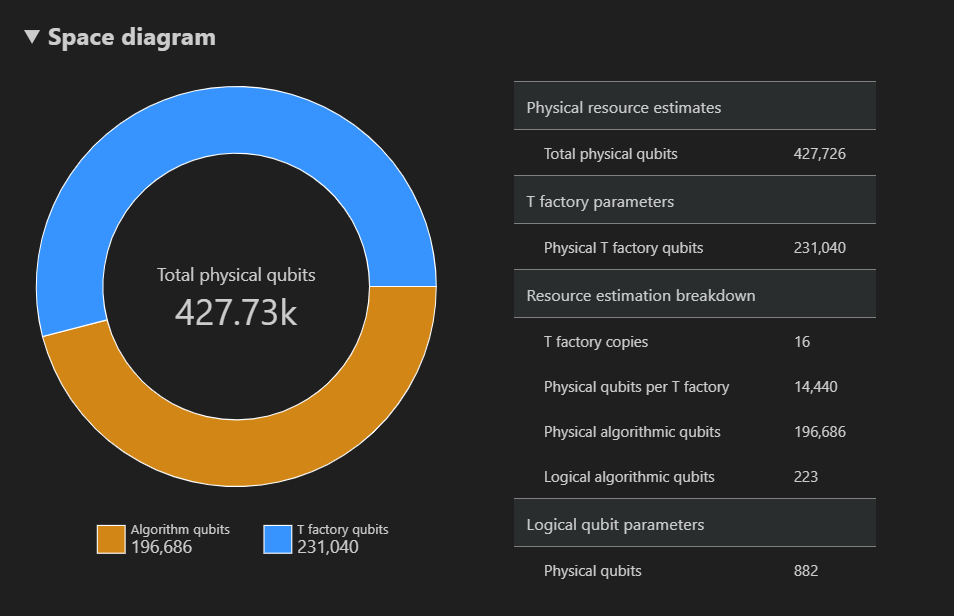
最后，“ 资源估算 ”选项卡显示与 {数量的量子比特、运行时} 对对应的资源估算器输出数据的完整列表。可以通过折叠包含更多信息的组来检查成本详细信息。例如，在空间关系图中选择最左侧的点，然后折叠 逻辑量子比特参数 组。

逻辑量子比特参数	值
QEC 方案	surface_code
码距	21
物理量子比特	882
逻辑周期时间	13 毫升
逻辑量子比特错误率	3.00E-13
交叉预制	0.03
错误更正阈值	0.01
逻辑周期时间公式	(4 * `twoQubitGateTime` + 2 * `oneQubitMeasurementTime`) * `codeDistance`
物理量子比特公式	2 * `codeDistance` * `codeDistance`

提示

单击“显示详细行”可显示报表数据的每个输出的说明。

有关详细信息，请参阅资源估算器的完整报表数据。

target更改参数

可以使用其他量子比特类型、更正代码和错误预算来估算同一 Q# 程序的成本。通过选择“视图 -> 命令面板”打开“资源估算器”窗口，然后键入Q#: Calculate Resource Estimates。

选择任何其他配置，例如基于 Majorana 的量子比特参数 qubit_maj_ns_e6。接受默认错误预算值或输入新值，然后按 Enter。资源估算器使用新 target 参数重新运行估算。

有关详细信息，请参阅 Target 资源估算器的参数。

运行多个参数配置

Azure Quantum 资源估算器可以运行多个参数配置 target ，并比较资源估算结果。

选择 视图 -> 命令面板，或按 Ctrl+Shift+P，然后键入 Q#: Calculate Resource Estimates。
选择qubit_gate_us_e3、qubit_gate_us_e4、qubit_maj_ns_e4 + floquet_code，然后qubit_maj_ns_e6 + floquet_code，然后单击“确定”。
接受默认错误预算值 0.001，然后按 Enter。
按 Enter 接受输入文件，在本例中为 ShorRE.qs。
对于多个参数配置，结果将显示在“结果”选项卡中的不同行中。
空间图显示所有参数配置的结果。结果表的第一列显示每个参数配置的图例。可以将鼠标悬停在每个点上以查看该点的资源估算的详细信息。
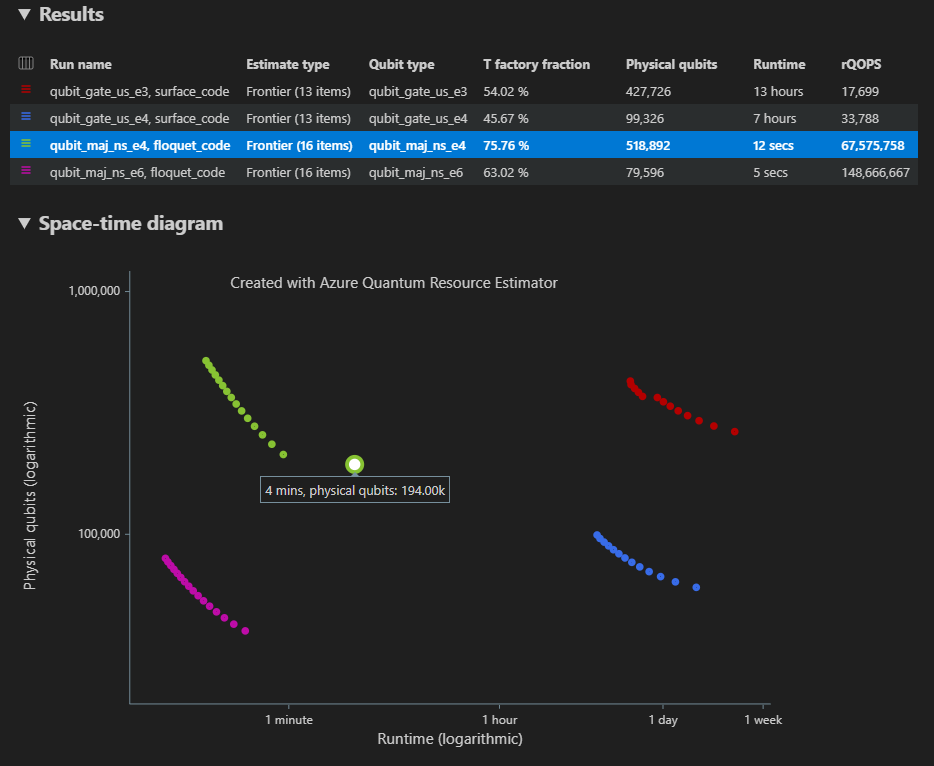
单击 空间图的 {数量的量子比特，运行时} 点 以显示相应的空间图和报告数据。

VS Code 中 Jupyter Notebook 的先决条件

安装了 Python 和 Pip 的 Python 环境。
最新版本的 Visual Studio Code 或打开网页版 VS Code。
安装了 Azure Quantum 开发工具包、Python 和 Jupyter 扩展的 VS Code。

最新的 Azure Quantum qsharp 和 qsharp-widgets 包。

python -m pip install --upgrade qsharp qsharp-widgets

提示

无需有 Azure 帐户即可运行本地资源估算器。

创建量子算法

在 VS Code 中，选择“视图 > 命令面板”，然后选择“创建：新 Jupyter Notebook”。
在右上角，VS Code 将检测并显示为笔记本选择的 Python 版本和虚拟 Python 环境。如果有多个 Python 环境，可能需要使用右上角的内核选取器选择内核。如果未检测到任何环境，请参阅 VS Code 中的 Jupyter Notebook 以获取设置信息。
在笔记本的第一个单元格中，导入 qsharp 包。
```
import qsharp
```

添加新单元格并复制以下代码。

%%qsharp
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;

operation RunProgram() : Unit {
    let bitsize = 31;

    // When choosing parameters for `EstimateFrequency`, make sure that
    // generator and modules are not co-prime
    let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}


// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.

/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
    generator : Int,
    modulus : Int,
    bitsize : Int
)
: Int {
    mutable frequencyEstimate = 0;
    let bitsPrecision =  2 * bitsize + 1;

    // Allocate qubits for the superposition of eigenstates of
    // the oracle that is used in period finding.
    use eigenstateRegister = Qubit[bitsize];

    // Initialize eigenstateRegister to 1, which is a superposition of
    // the eigenstates we are estimating the phases of.
    // We first interpret the register as encoding an unsigned integer
    // in little endian encoding.
    ApplyXorInPlace(1, eigenstateRegister);
    let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);

    // Use phase estimation with a semiclassical Fourier transform to
    // estimate the frequency.
    use c = Qubit();
    for idx in bitsPrecision - 1..-1..0 {
        within {
            H(c);
        } apply {
            // `BeginEstimateCaching` and `EndEstimateCaching` are the operations
            // exposed by Azure Quantum Resource Estimator. These will instruct
            // resource counting such that the if-block will be executed
            // only once, its resources will be cached, and appended in
            // every other iteration.
            if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
                Controlled oracle([c], (1 <<< idx, eigenstateRegister));
                EndEstimateCaching();
            }
            R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
        }
        if MResetZ(c) == One {
            set frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
        }
    }

    // Return all the qubits used for oracle eigenstate back to 0 state
    // using Microsoft.Quantum.Intrinsic.ResetAll.
    ResetAll(eigenstateRegister);

    return frequencyEstimate;
}

/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
    generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
    // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
    // also use `ExpModI` to compute a by which x must be multiplied. Also
    // note that we interpret target as unsigned integer in little-endian
    // encoding.
    ModularMultiplyByConstant(modulus,
                                ExpModI(generator, power, modulus),
                                target);
}

/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
    use qs = Qubit[Length(y)];
    for (idx, yq) in Enumerated(y) {
        let shiftedC = (c <<< idx) % modulus;
        Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
    }
    ApplyToEachCA(SWAP, Zipped(y, qs));
    let invC = InverseModI(c, modulus);
    for (idx, yq) in Enumerated(y) {
        let shiftedC = (invC <<< idx) % modulus;
        Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
    }
}

/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register  |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
    body (...) {
        Controlled ModularAddConstant([], (modulus, c, y));
    }
    controlled (ctrls, ...) {
        // We apply a custom strategy to control this operation instead of
        // letting the compiler create the controlled variant for us in which
        // the `Controlled` functor would be distributed over each operation
        // in the body.
        //
        // Here we can use some scratch memory to save ensure that at most one
        // control qubit is used for costly operations such as `AddConstant`
        // and `CompareGreaterThenOrEqualConstant`.
        if Length(ctrls) >= 2 {
            use control = Qubit();
            within {
                Controlled X(ctrls, control);
            } apply {
                Controlled ModularAddConstant([control], (modulus, c, y));
            }
        } else {
            use carry = Qubit();
            Controlled AddConstant(ctrls, (c, y + [carry]));
            Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
            Controlled AddConstant([carry], (modulus, y));
            Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
        }
    }
}

/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
    // We are using this version instead of the library version that is based
    // on Fourier angles to show an advantage of sparse simulation in this sample.

    let n = Length(y);
    Fact(n > 0, "Bit width must be at least 1");

    Fact(c >= 0, "constant must not be negative");
    Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");

    if c != 0 {
        // If c has j trailing zeroes than the j least significant bits
        // of y will not be affected by the addition and can therefore be
        // ignored by applying the addition only to the other qubits and
        // shifting c accordingly.
        let j = NTrailingZeroes(c);
        use x = Qubit[n - j];
        within {
            ApplyXorInPlace(c >>> j, x);
        } apply {
            IncByLE(x, y[j...]);
        }
    }
}

/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
    let bitWidth = Length(x);

    if c == 0 {
        X(target);
    } elif c >= 2 ^ bitWidth {
        // do nothing
    } elif c == 2 ^ (bitWidth - 1) {
        ApplyLowTCNOT(Tail(x), target);
    } else {
        // normalize constant
        let l = NTrailingZeroes(c);

        let cNormalized = c >>> l;
        let xNormalized = x[l...];
        let bitWidthNormalized = Length(xNormalized);
        let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));

        use qs = Qubit[bitWidthNormalized - 1];
        let cs1 = [Head(xNormalized)] + Most(qs);
        let cs2 = Rest(xNormalized);

        within {
            for i in IndexRange(gates) {
                (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
            }
        } apply {
            ApplyLowTCNOT(Tail(qs), target);
        }
    }
}

/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
    within {
        ApplyToEachA(X, [control1, control2]);
    } apply {
        ApplyAnd(control1, control2, target);
        X(target);
    }
}

internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
    body (...) {
        CCNOT(control1, control2, target);
    }
    adjoint (...) {
        H(target);
        if (M(target) == One) {
            X(target);
            CZ(control1, control2);
        }
    }
}


/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
    mutable nZeroes = 0;
    mutable copy = number;
    while (copy % 2 == 0) {
        set nZeroes += 1;
        set copy /= 2;
    }
    return nZeroes;
}

/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
    body (...) {
        CNOT(a, b);
    }

    adjoint self;

    controlled (ctls, ...) {
        // In this application this operation is used in a way that
        // it is controlled by at most one qubit.
        Fact(Length(ctls) <= 1, "At most one control line allowed");

        if IsEmpty(ctls) {
            CNOT(a, b);
        } else {
            use q = Qubit();
            within {
                ApplyAnd(Head(ctls), a, q);
            } apply {
                CNOT(q, b);
            }
        }
    }

    controlled adjoint self;
}

估计量子算法

现在使用默认假设来估算 RunProgram 操作的物理资源。添加新单元格并复制以下代码。

result = qsharp.estimate("RunProgram()")
result

qsharp.estimate 函数创建一个结果对象，可用于显示整体物理资源计数的表。可以通过折叠包含更多信息的组来检查成本详细信息。有关详细信息，请参阅资源估算器的完整报表数据。

例如，折叠“逻辑量子比特参数”组以查看代码距离为 21，物理量子比特数为 882。

逻辑量子比特参数	值
QEC 方案	surface_code
码距	21
物理量子比特	882
逻辑周期时间	8 毫升
逻辑量子比特错误率	3.00E-13
交叉预制	0.03
错误更正阈值	0.01
逻辑周期时间公式	(4 * `twoQubitGateTime` + 2 * `oneQubitMeasurementTime`) * `codeDistance`
物理量子比特公式	2 * `codeDistance` * `codeDistance`

提示

对于更紧凑的输出表，可以使用 result.summary。

空间图

用于算法和 T 工厂的物理量子比特的分布可能会影响算法设计。可以使用 qsharp-widgets 包来可视化此分布，以便更好地了解算法的预计空间要求。

from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)

在此示例中，运行算法所需的物理量子比特数为 829766，其中 196686 个是算法量子比特，633080 个是 T 工厂量子比特。

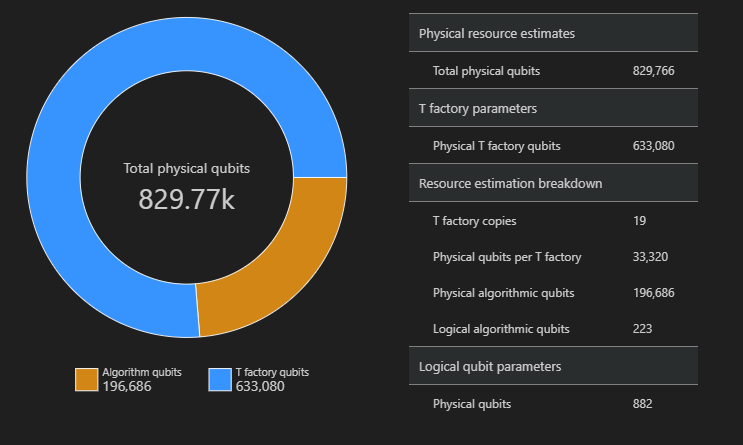
显示资源估算器空间图的屏幕截图。

更改默认值并估计算法

为程序提交资源估算请求时，可以指定一些可选参数。使用 jobParams 字段访问可传递给作业执行的所有 target 参数，并查看假定的默认值：

result['jobParams']

{'errorBudget': 0.001,
 'qecScheme': {'crossingPrefactor': 0.03,
  'errorCorrectionThreshold': 0.01,
  'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
  'name': 'surface_code',
  'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
 'qubitParams': {'instructionSet': 'GateBased',
  'name': 'qubit_gate_ns_e3',
  'oneQubitGateErrorRate': 0.001,
  'oneQubitGateTime': '50 ns',
  'oneQubitMeasurementErrorRate': 0.001,
  'oneQubitMeasurementTime': '100 ns',
  'tGateErrorRate': 0.001,
  'tGateTime': '50 ns',
  'twoQubitGateErrorRate': 0.001,
  'twoQubitGateTime': '50 ns'}}

可以看到，资源估算器采用了 qubit_gate_ns_e3 量子比特模型、surface_code 纠错代码和 0.001 错误预算作为估算的默认值。

以下是 target 可以自定义的参数：

errorBudget - 算法的总体允许错误预算
qecScheme - 量子纠错 (QEC) 方案
qubitParams - 物理量子比特参数
constraints - 组件级约束
distillationUnitSpecifications - T 工厂蒸馏算法的规范
estimateType - 单一或边界

有关详细信息，请参阅 Target 资源估算器的参数。

更改量子比特模型

可以使用基于 Majorana 的量子比特参数 qubitParams“qubit_maj_ns_e6”估算同一算法的成本。

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                }})
EstimateDetails(result_maj)

更改量子纠错方案

对于基于 Majorana 的量子比特参数上的同一示例，可以使用已 floque 的 QEC 方案 qecScheme 重新运行资源估算作业。

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                },
                "qecScheme": {
                    "name": "floquet_code"
                }})
EstimateDetails(result_maj)

更改错误预算

接下来，使用 10% 的 errorBudget 重新运行同一量子线路。

result_maj = qsharp.estimate("RunProgram()", params={
                "qubitParams": {
                    "name": "qubit_maj_ns_e6"
                },
                "qecScheme": {
                    "name": "floquet_code"
                },
                "errorBudget": 0.1})
EstimateDetails(result_maj)

使用资源估算器进行批处理

Azure Quantum 资源估算器允许运行多个参数配置 target ，并比较结果。如果要比较不同量子比特模型、QEC 方案或错误预算的成本，这会非常有用。

可以通过将参数params列表target传递给函数的参数qsharp.estimate来执行批处理估计。例如，使用默认参数和基于 Majorana 的量子比特参数运行同一算法，并使用 floquet QEC 方案。

result_batch = qsharp.estimate("RunProgram()", params=
                [{}, # Default parameters
                {
                    "qubitParams": {
                        "name": "qubit_maj_ns_e6"
                    },
                    "qecScheme": {
                        "name": "floquet_code"
                    }
                }])
result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])

型号	逻辑量子比特	逻辑深度	T 状态	码距	T 工厂	T 工厂分数	物理量子比特	rQOPS	物理运行时
基于门的 ns，10⁻³	223	3.64M	4.70M	21	19	76.30 %	829.77k	26.55M	31 秒
Majorana ns，10⁻⁶	223	3.64M	4.70M	5	19	63.02 %	79.60k	148.67M	5 秒

还可以使用 EstimatorParams 类构造估计参数列表。

from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts

labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"]

params = EstimatorParams(num_items=6)
params.error_budget = 0.333
params.items[0].qubit_params.name = QubitParams.GATE_US_E3
params.items[1].qubit_params.name = QubitParams.GATE_US_E4
params.items[2].qubit_params.name = QubitParams.GATE_NS_E3
params.items[3].qubit_params.name = QubitParams.GATE_NS_E4
params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4
params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE
params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6
params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODE

qsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)

型号	逻辑量子比特	逻辑深度	T 状态	码距	T 工厂	T 工厂分数	物理量子比特	rQOPS	物理运行时
基于门的 µs，10⁻³	223 3.64M	4.70M	17	13	40.54%	216.77k	21.86k	10 小时
基于门的 µs，10⁻⁴	223	3.64M	4.70M	9	14	43.17%	63.57k	41.30k	5 小时
基于门的 ns，10⁻³	223 3.64M	4.70M	17	16	69.08%	416.89k	32.79M	25 秒
基于门的 ns，10⁻⁴	223 3.64M	4.70M	9	14	43.17%	63.57k	61.94M	13 秒
Majorana ns，10⁻⁴	223 3.64M	4.70M	9	19	82.75%	501.48k	82.59M	10 秒
Majorana ns，10⁻⁶	223 3.64M	4.70M	5	13	31.47%	42.96k	148.67M	5 秒

运行 Pareto 边界估计

估算算法的资源时，请务必考虑物理量子比特数与算法运行时之间的权衡。可以考虑分配尽可能多的物理量子比特以减少算法的运行时。但是，物理量子比特的数量受量子硬件中可用的物理量子比特数的限制。

Pareto 边界估计为同一算法提供了多个估计值，每个算法在量子比特数和运行时之间进行权衡。

若要使用 Pareto 边界估计运行资源估算器，需要将参数指定 "estimateType"target 为 "frontier"。例如，使用 Pareto 边界估计，使用基于 Majorana 的量子比特参数运行同一算法，并使用图面代码。

result = qsharp.estimate("RunProgram()", params=
                            {"qubitParams": { "name": "qubit_maj_ns_e4" },
                            "qecScheme": { "name": "surface_code" },
                            "estimateType": "frontier", # frontier estimation
                            }
                        )

可以使用函数 EstimatesOverview 显示具有整体物理资源计数的表。单击第一行旁边的图标，选择要显示的列。可以从运行名称、估计类型、量子比特类型、qec 方案、错误预算、逻辑量子比特、逻辑深度、代码距离、T 状态、T 工厂、T 工厂、T 工厂分数、运行时、rQOPS 和物理量子比特中进行选择。
```
from qsharp_widgets import EstimatesOverview
EstimatesOverview(result)
```

在 结果表的“估计类型 ”列中，可以看到算法的 {量子比特数，运行时} 的不同组合数。在这种情况下，资源估算器发现 22 个不同的最佳组合数千个可能的组合。

时空关系图

该 EstimatesOverview 函数还显示资源估算器的时空关系图。

空间时间关系图显示每个 {量子比特数，运行时} 对的物理量子比特数和算法的运行时。可以将鼠标悬停在每个点上以查看该点的资源估算的详细信息。

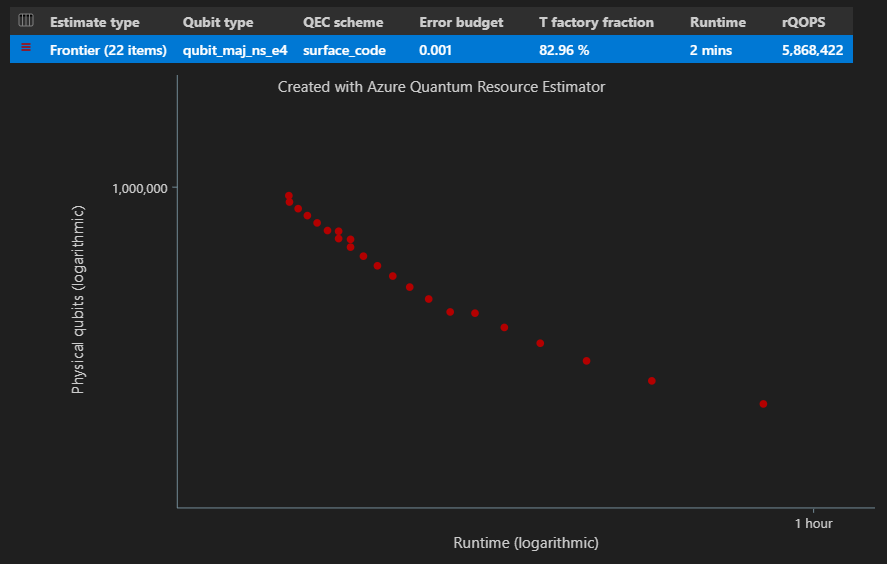
显示空间时间关系图的屏幕截图，其中边距估计器为资源估算器。

使用 Pareto 边界估计进行批处理

若要估算和比较多个参数配置 target 与边界估计，请添加到 "estimateType": "frontier", 参数中。

result = qsharp.estimate(
    "RunProgram()",
    [
        {
        "qubitParams": { "name": "qubit_maj_ns_e4" },
        "qecScheme": { "name": "surface_code" },
        "estimateType": "frontier", # Pareto frontier estimation
        },
        {
        "qubitParams": { "name": "qubit_maj_ns_e6" },
        "qecScheme": { "name": "floquet_code" },
        "estimateType": "frontier", # Pareto frontier estimation
        },
    ]
)

EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])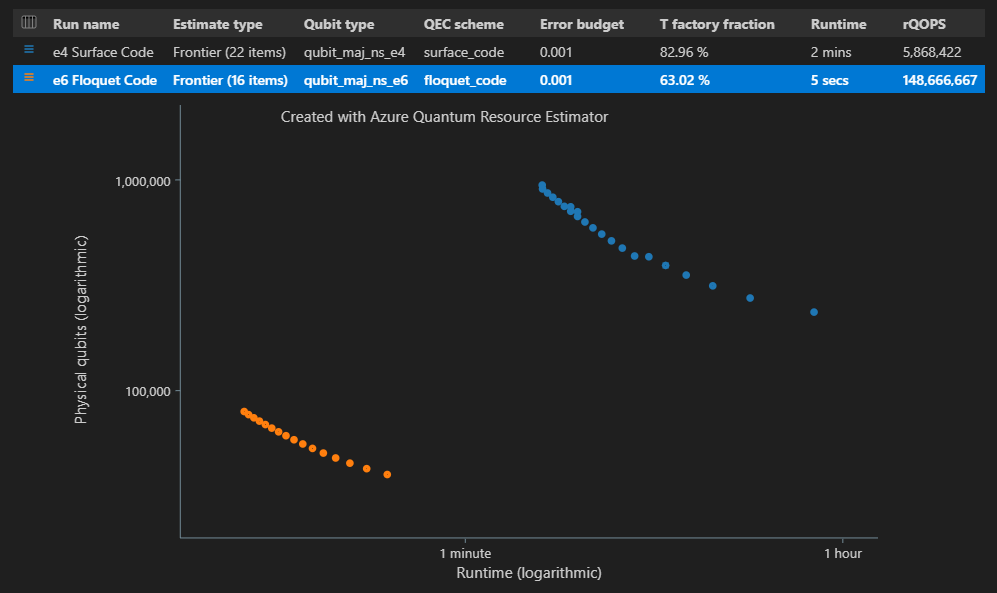

显示使用 Pareto 边界估算和多个参数配置时资源估算器的空间图示的屏幕截图。

注意

可以使用函数 EstimatesOverview 定义量子比特时间关系图的颜色和运行名称。

使用 Pareto 边界估计运行多个参数配置 target 时，可以看到空间图的特定时间点的资源估计值，即每个 {量子比特数、运行时} 对。例如，以下代码显示第二个（estimate index=0）运行和第四个（point index=3）最短运行时的估计详细信息使用情况。
```
EstimateDetails(result[1], 4)
```
还可以查看空间图中特定时间点的空间关系图。例如，以下代码显示了第一次运行组合（估计索引=0）和第三个最短运行时（点索引=2）的空间图。
```
SpaceChart(result[0], 2)
```

Qiskit 的先决条件

具有活动订阅的 Azure 帐户。如果没有 Azure 帐户，请免费注册并注册即用即付订阅。
Azure Quantum 工作区。有关详细信息，请参阅创建 Azure Quantum 工作区。

在工作区中启用 Azure Quantum 资源估算器target

资源估算器是 target Microsoft量子计算提供程序。如果自资源估算器发布后创建了工作区，则会自动将 Microsoft Quantum Computing 提供程序添加到工作区。

如果使用 现有的 Azure Quantum 工作区：

在 Azure 门户中打开你的工作区。
在左侧面板的“操作”下，选择“提供程序”。
选择“+ 添加提供程序”。
为“Microsoft 量子计算”选择“+ 添加”。
选择 “学习和开发 ”，然后选择“ 添加”。

在工作区中创建新的笔记本

登录到 Azure 门户并选择你的 Azure Quantum 工作区。
在“操作”下，选择“笔记本”
单击“我的笔记本”，然后单击“添加新”
在“内核类型”中选择“IPython”。
键入文件的名称，然后单击“ 创建文件”。

当你的新笔记本打开时，它会根据订阅和工作区信息自动为第一个单元格创建代码。

from azure.quantum import Workspace
workspace = Workspace ( 
    resource_id = "", # Your resource_id 
    location = ""  # Your workspace location (for example, "westus") 
)

注意

除非另有说明，否则应按照单元的创建顺序运行每个单元，以避免任何编译问题。

单击单元左侧的三角形“播放”图标以运行代码。

加载所需的导入项

首先，需要从 azure-quantum 和 qiskit..

单击“+ 代码”添加一个新的单元，然后添加并运行以下代码：

from azure.quantum.qiskit import AzureQuantumProvider
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library import RGQFTMultiplier

连接到 Azure Quantum 服务

接下来，使用workspace上一单元格中的对象创建一个 AzureQuantumProvider 对象，以连接到 Azure Quantum 工作区。创建后端实例并将资源估算器设置为你的 target。

provider = AzureQuantumProvider(workspace)
backend = provider.get_backend('microsoft.estimator')

创建量子算法

在此示例中，将基于 Ruiz-Perez 和 Garcia-Escartin（arXiv：1411.5949）中显示的构造（使用 Quantum Fourier Transform 实现算术）为乘数创建量子线路。

可以通过更改 bitwidth 变量来调整乘数的大小。线路生成包装在可以使用乘数值调用 bitwidth 的函数中。该操作将有两个输入寄存器，每个输入寄存器的大小指定 bitwidth，一个输出寄存器是指定 bitwidth大小的两倍。该函数还将输出直接从量子线路中提取的乘数的一些逻辑资源计数。

def create_algorithm(bitwidth):
    print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
    
    # Print a warning for large bitwidths that will require some time to generate and
    # transpile the circuit.
    if bitwidth > 18:
        print(f"[WARN] It will take more than one minute generate a quantum circuit with a bitwidth larger than 18")

    circ = RGQFTMultiplier(num_state_qubits=bitwidth, num_result_qubits=2 * bitwidth)

    # One could further reduce the resource estimates by increasing the optimization_level,
    # however, this will also increase the runtime to construct the algorithm.  Note, that
    # it does not affect the runtime for resource estimation.
    print(f"[INFO] Decompose circuit into intrinsic quantum operations")

    circ = transpile(circ, basis_gates=SUPPORTED_INSTRUCTIONS, optimization_level=0)

    # print some statistics
    print(f"[INFO]   qubit count: {circ.num_qubits}")
    print("[INFO]   gate counts")
    for gate, count in circ.count_ops().items():
        print(f"[INFO]   - {gate}: {count}")

    return circ

注意

可以为没有 T 状态但至少具有一个度量的算法提交物理资源估算作业。

估计量子算法

使用 create_algorithm 函数创建算法的实例。可以通过更改 bitwidth 变量来调整乘数的大小。

bitwidth = 4

circ = create_algorithm(bitwidth)

使用默认假设估算此操作的物理资源。可以使用该方法将线路提交到资源估算器后端 run ，然后运行 job.result() 以等待作业完成并返回结果。

job = backend.run(circ)
result = job.result()
result

这会创建一个表，其中显示了总体物理资源计数。可以通过折叠包含更多信息的组来检查成本详细信息。

提示

对于更紧凑的输出表，可以使用 result.summary。

例如，如果折叠 逻辑量子比特参数 组，则更容易看到错误更正代码距离为 15。

逻辑量子比特参数	值
QEC 方案	surface_code
码距	15
物理量子比特	450
逻辑周期时间	6us
逻辑量子比特错误率	3.00E-10
交叉预制	0.03
错误更正阈值	0.01
逻辑周期时间公式	(4 * `twoQubitGateTime` + 2 * `oneQubitMeasurementTime`) * `codeDistance`
物理量子比特公式	2 * `codeDistance` * `codeDistance`

在 物理量子比特参数 组中，可以看到假定用于此估计的物理量子比特属性。例如，执行单量子比特测量和单量子比特门的时间分别假设为 100 ns 和 50 ns。

提示

还可以使用 result.data（）方法以 Python 字典的形式访问资源估算器的输出。

有关详细信息，请参阅资源估算器输出数据的完整列表。

空间图

用于算法和 T 工厂的物理量子比特的分布可能会影响算法设计。可以将此分布可视化，以便更好地了解算法的估计空间要求。

result.diagram.space

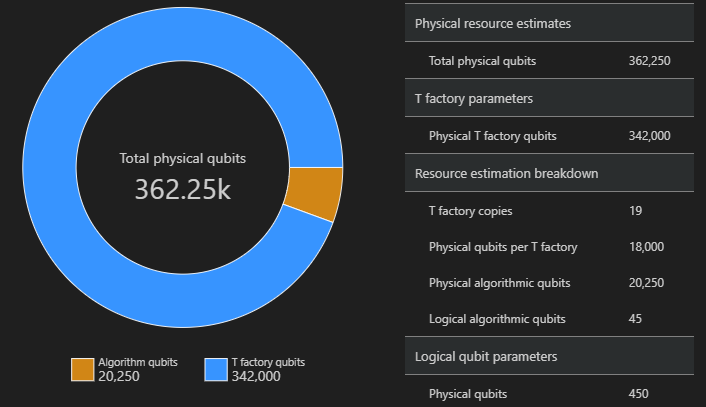
显示算法量子比特和 T 工厂量子比特之间的总物理量子比特分布的饼图。有一个表，其中细分了每个 T 工厂的 T 工厂副本数和物理量子比特数。

空间图显示了算法量子比特和 T 工厂量子比特的比例。请注意，作为 $\text{T factories} \cdot \text{physical qubit per T factory}= 28 \cdot 18,000 = 504,000$ 为 T 工厂的物理量子比特数，T 工厂副本数为 $\text{T factories} \cdot \text{physical qubit per T factory}= 28 \cdot 18,000 = 504,000$。

有关详细信息，请参阅 T 工厂物理估计。

更改默认值并估计算法

为程序提交资源估算请求时，可以指定一些可选参数。使用 jobParams 字段访问可传递给作业执行的所有值，并查看假定的默认值：

result.data()["jobParams"]

{'errorBudget': 0.001,
 'qecScheme': {'crossingPrefactor': 0.03,
  'errorCorrectionThreshold': 0.01,
  'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
  'name': 'surface_code',
  'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
 'qubitParams': {'instructionSet': 'GateBased',
  'name': 'qubit_gate_ns_e3',
  'oneQubitGateErrorRate': 0.001,
  'oneQubitGateTime': '50 ns',
  'oneQubitMeasurementErrorRate': 0.001,
  'oneQubitMeasurementTime': '100 ns',
  'tGateErrorRate': 0.001,
  'tGateTime': '50 ns',
  'twoQubitGateErrorRate': 0.001,
  'twoQubitGateTime': '50 ns'}}

以下是 target 可以自定义的参数：

errorBudget - 总体允许的错误预算
qecScheme - 量子纠错 (QEC) 方案
qubitParams - 物理量子比特参数
constraints - 组件级约束
distillationUnitSpecifications - T 工厂蒸馏算法的规范

有关详细信息，请参阅 Target 资源估算器的参数。

更改量子比特模型

接下来，使用基于 Majorana 的量子比特参数估算同一算法的成本 qubit_maj_ns_e6

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    })
result = job.result()
result

可以编程方式检查物理计数。例如，可以浏览有关创建以执行算法的 T 工厂的详细信息。

result.data()["tfactory"]

{'eccDistancePerRound': [1, 1, 5],
 'logicalErrorRate': 1.6833177305222897e-10,
 'moduleNamePerRound': ['15-to-1 space efficient physical',
  '15-to-1 RM prep physical',
  '15-to-1 RM prep logical'],
 'numInputTstates': 20520,
 'numModulesPerRound': [1368, 20, 1],
 'numRounds': 3,
 'numTstates': 1,
 'physicalQubits': 16416,
 'physicalQubitsPerRound': [12, 31, 1550],
 'runtime': 116900.0,
 'runtimePerRound': [4500.0, 2400.0, 110000.0]}

注意

默认情况下，运行时以纳秒为单位显示。

可以使用此数据生成一些说明，说明 T 工厂如何生成所需的 T 状态。

data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]

print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
    print(f"""- {tfactory["numModulesPerRound"][round]} {tfactory["moduleNamePerRound"][round]} unit(s)""")

A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)

更改量子纠错方案

现在，使用软盘 QEC 方案 qecScheme重新运行基于 Majorana 的量子比特参数上的同一示例的资源估算作业。

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    },
    qecScheme={
        "name": "floquet_code"
    })
result_maj_floquet = job.result()
result_maj_floquet

更改错误预算

让我们重新运行一个 10% 的同一 errorBudget 量子线路。

job = backend.run(circ,
    qubitParams={
        "name": "qubit_maj_ns_e6"
    },
    qecScheme={
        "name": "floquet_code"
    },
    errorBudget=0.1)
result_maj_floquet_e1 = job.result()
result_maj_floquet_e1

注意

如果在使用资源估算器时遇到任何问题，请查看 “故障排除”页或联系 AzureQuantumInfo@microsoft.com。

通过

运行资源估算器的不同方式

VS Code 的先决条件

创建新的 Q# 文件

创建量子算法

运行资源估算器

查看结果

target更改参数

运行多个参数配置

VS Code 中 Jupyter Notebook 的先决条件

创建量子算法

估计量子算法

空间图

更改默认值并估计算法

更改量子比特模型

更改量子纠错方案

更改错误预算

使用资源估算器进行批处理

运行 Pareto 边界估计

时空关系图

使用 Pareto 边界估计进行批处理

Qiskit 的先决条件

在工作区中启用 Azure Quantum 资源估算器target

在工作区中创建新的笔记本

加载所需的导入项

连接到 Azure Quantum 服务

创建量子算法

估计量子算法

空间图

更改默认值并估计算法

更改量子比特模型

更改量子纠错方案

更改错误预算

后续步骤

反馈

其他资源