你当前正在访问 Microsoft Azure Global Edition 技术文档网站。 如果需要访问由世纪互联运营的 Microsoft Azure 中国技术文档网站,请访问 https://docs.azure.cn。
Grover 搜索算法理论
本文从理论角度详细说明了支持 Grover 算法运作的数学原理。
有关 Grover 算法解决数学问题的实用实现,请参阅 Implement Grover 的搜索算法。
问题陈述
Grover 的算法加快了非结构化数据搜索(或 搜索问题)的解决方案,以比任何经典算法更少的步骤运行搜索。 任何搜索任务都可以使用抽象函数 $f(x)$ 表示,该函数接受搜索项 $x$。 如果项 $x$ 是搜索任务的解,则 $f(x)=1$。 如果项 $x$ 不是解,则 $f(x)=0$。 搜索问题包括查找使 $f(x_0)$1$ 的任何项 =x_0$。
任何允许你检查给定值 $x$是否是有效解决方案的问题(&“是或否问题”&)都可以用搜索问题来表述。 下面是一些示例:
- 布尔可满足性问题:给定一组布尔值后,该集是否满足给定布尔公式?
- 旅行推销员问题:连接所有城市的最短路径是什么?
- 数据库搜索问题:数据库表是否包含 $x$记录?
- 整数分解问题:数字 $N$ 是否由数字 $x$分割?
Grover 算法旨在解决的任务可以表示如下:给定经典函数 $f(x):\{0,1\}^n \rightarrow\{0,1\}$,其中 $n$ 是搜索空间的比特大小,找到使 $f(x_0)$1$ 的输入 =x_0$。 此算法的复杂度是通过函数 $f(x)$ 的使用次数衡量的。 传统上,在最糟糕的情况下,需要总共计算 $f(x)$$N-1$ 次,其中 $N=2^n$,以尝试所有可能性。 $N-1$ 个元素之后,它肯定是最后一个元素。 Grover 量子算法能够更快速地解决此问题,实现了二次加速。 此处的“二次”表示,只需大约 $\sqrt{N}$ 次计算,而不是 $N$ 次。
算法概述
假设搜索任务有 $N=2^n$ 个符合条件的项,并且为每个项目分配一个从 $0$ 到 $N-1$ 的整数来为它们编制索引。 此外,假设有 $M$ 个不同的有效输入,也就是说,有 $M$ 个输入的 $f(x)=1$。 这样一来,算法的步骤如下所示:
- 从以状态 $ 初始化的 $n$\ket{0}$ 个量子比特的寄存器开始。
- 通过向寄存器中的每个量子比特应用 $H$,准备将寄存器均匀叠加:$$|\text{register}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|x\rangle$$
- 将以下操作应用于寄存器 $N_{\text{optimal}}$ 次:
- 为求解项应用条件相移为 $-1$ 的相位黑盒 $O_f$。
- 向寄存器中的每个量子比特应用 $H$。
- 应用于除 $ 之外的每个计算基础状态的条件相移 $-1$\ket{0}$。 这可以由单一运算 $-O_0$ 表示,因为 $O_0$ 只表示对 $\ket{0}$ 的条件相移。
- 向寄存器中的每个量子比特应用 $H$。
- 度量寄存器以获取具有很高概率为解的项的索引。
- 检查它是否为有效的解。 如果不是,则再次开始运算。
$N_{\text{optimal}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{{2}\right\rfloor$ 是通过测量寄存器来最大程度提高获得正确项的可能性的最佳迭代次数。
注意
步骤 3.b、3.c 和 3.d 的联合应用通常称为 Grover 的扩散运算符。
向寄存器应用的整个单一运算为:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$
逐步跟踪寄存器的状态
为说明此过程,我们将跟踪一个简单情况下的寄存器状态的数学转换,其中只有两个量子比特,并且有效元素为 $\ket{01}。$
寄存器在以下状态下启动:
$\ket{\text{register}}=\ket{{00}$
将 $H$ 应用于每个量子位后,寄存器的状态将转换为:
$\ket{\text{register}}=\frac{{1}{\sqrt{4}}\sum_{i \in \lbrace 0,1 \rbrace}^2\ket{i}=\frac12(\ket{00}+\ket{01}+\ket{{10}+\ket{11})$
然后,应用相位黑盒来获取:
$\ket{\text{register}}=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$
然后,$H$ 再次对每个量子比特起作用,以便提供:
$\ket{\text{register}}=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$
现在,条件阶段转移将应用于除 $\ket{00}$以外的每个状态:
$\ket{\text{register}}=\frac12(\ket{{00}-\ket{{01}+\ket{{10}-\ket{{11})$
最后,第一个 Grover 迭代通过再次应用 $H$ 以获取以下项来结束:
$\ket{\text{register}}=\ket{{01}$
执行上述步骤,可以在单个迭代中找到有效项。 本节稍后你将会看到,这是因为对于 N=4 和单个有效项,最佳次数是 $N_{\text{optimal}}=1$。
几何学解释
为说明 Grover 算法为何有效,我们将从几何角度研究此算法。 假设有 $M$ 个有效解,即所有不是搜索问题的解的量子态的叠加:
$$\ket{\text{bad}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
所有是搜索问题的解的量子态的叠加:
$$\ket{\text{good}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
由于 good 和 bad 是互斥的集合(因为一个项目不能既有效又无效),所以状态是正交状态。 两种状态构成了向量空间中平面的正交基。 人们可以通过此平面将此算法可视化。
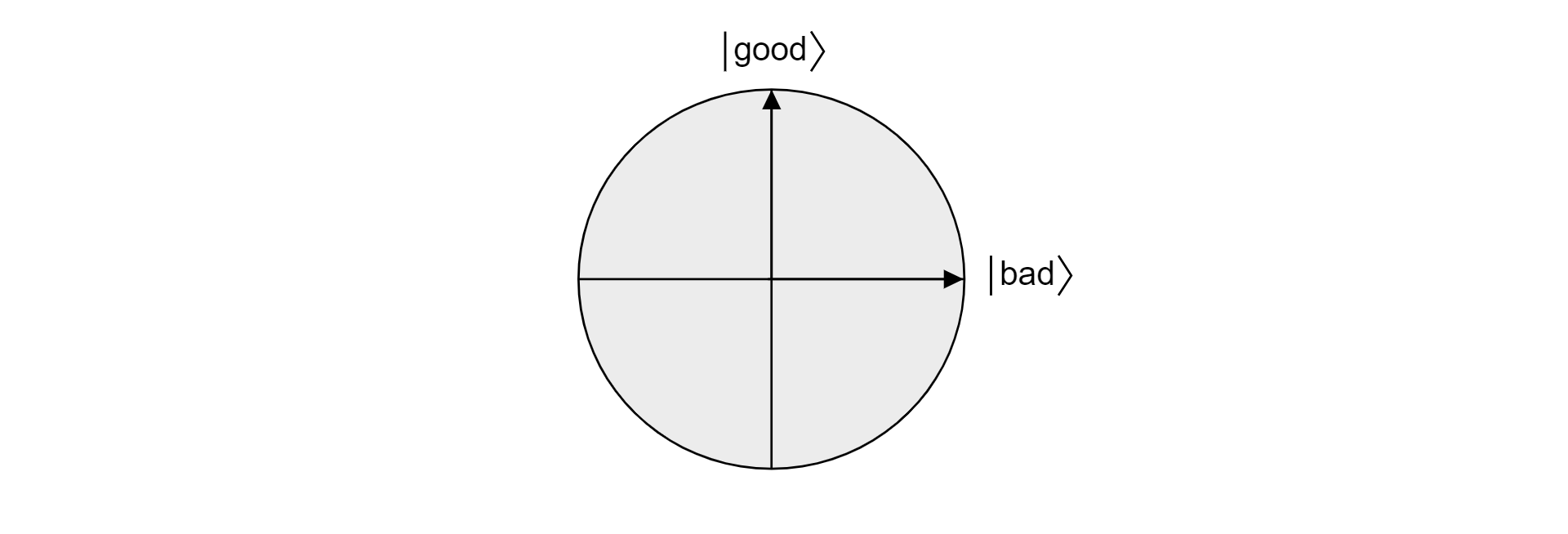
现在,假设 $\ket{\psi}$ 是跨越 $\ket{\text{good}}$ 和 $\ket{\text{bad}}$ 的平面中的一个任意的状态。 该平面中的任何状态都可表示为:
$$\ket{\psi}=\alpha\ket{\text{good}} + \beta\ket{\text{bad}}$$
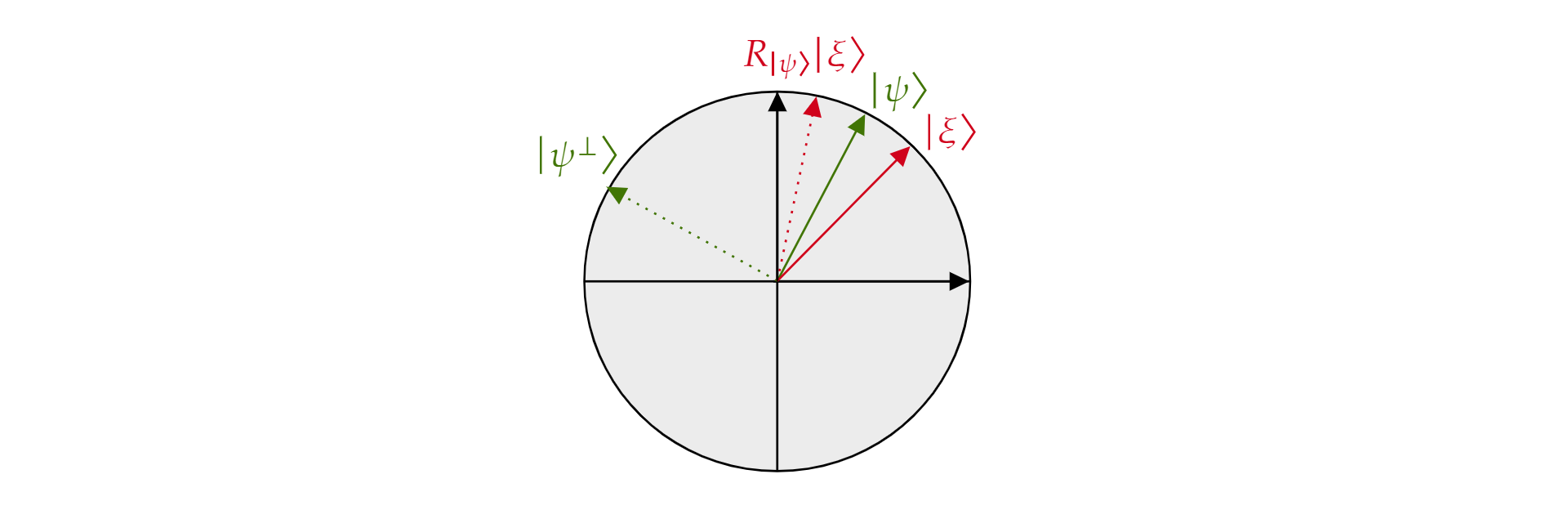
其中 $\alpha$ 和 $\beta$ 是实数。 接下来,我们介绍反射运算符 $R_{\ket{\psi}}$,其中 $\ket{\psi}$ 是此平面中的任意量子比特状态。 此运算符定义为:
$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$
它被称为关于 $\ket{\psi}$ 的反射运算符,因为在几何上可以将它解释为关于 $\ket{\psi}$ 的方向的反射。 请获取 $\ket{\psi}$ 和其正交互补 $\ket{\psi{}}$ 所形成的平面的正交基,以便于理解这一点。 此平面的任何状态 $\ket{\xi}$ 都可以基于此进行分解:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
如果将运算符 $R_{\ket{\psi}}$ 应用到 $\ket{\xi}$:
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
运算符 $R_{\ket{\psi}}$ 将与 $\ket{\psi}$ 正交的分量反转,但保留 $\ket{\psi}$ 分量不变。 因此,$R_{\ket{\psi}}$ 是关于 $\ket{\psi}$ 的反射。
在 Grover 算法中,第一次向每个量子比特应用 $H$ 后,会开始将所有状态均匀叠加。 这可表示为:
$$\ket{\text{all}}=\sqrt{\frac{M}{N}}\ket{\text{good}} + \sqrt{\frac{N-M}{N}}\ket{\text{bad}}$$
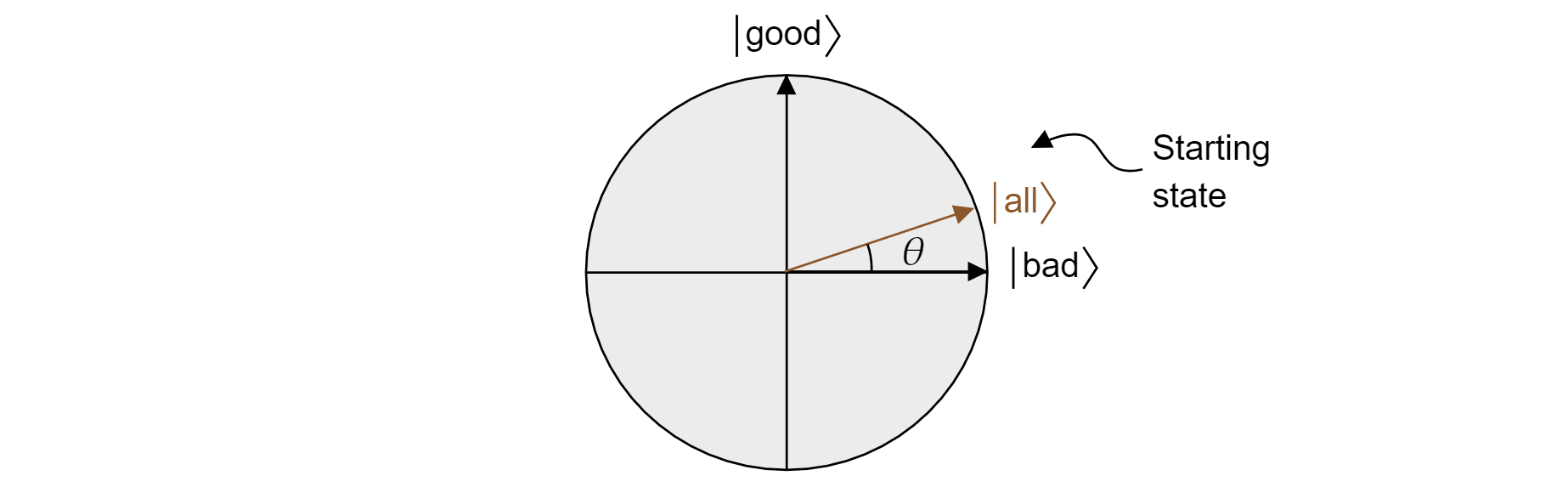
因此此状态在平面中存在。 请注意,从相等叠加测量时获取正确结果的概率只是 $|\bra{\text{好}}\ket{\text{所有}}|^2=M/N$,这是你期望随机猜测的结果。
黑盒 $O_f$ 向搜索问题的任意解添加一个负相。 因此,它可以表示为关于 $\ket{\text{bad}}$ 轴的反射:
$O_f = R_{\ket{\text{bad}}}= 2\ket{\text{bad}}\bra{\text{bad}} - \mathbb{I}$
同样,条件相移 $O_0$ 就是状态 $\ket{0}$ 的反转反射:
$O_{0}= R_{\ket{0}}= -2\ket{{0}\bra{{0} + \mathbb{I}$
了解了这个事实后,很容易检查 Grover 扩散运算 $-H^{\otimes n} O_{0} H^{\otimes n}$ 是关于 $\ket{all}$ 状态的反映。 只需执行:
$-H^{\otimes n} O_{{0} H^{\otimes n}=2H^{\otimes n}\ket{0}\bra{{0}H^{\otimes n} -H^{\otimes n}\mathbb{I}H^{\otimes n}= 2\ket{\text{all}}\bra{\text{all}} - \mathbb{I}= R_{\ket{\text{all}}}$
刚刚证明了 Grover 算法的每一次迭代都由 $R_{\ket{\text{bad}}}$ 和 $R_{\ket{\text{all}}}$ 这两个反射组成。
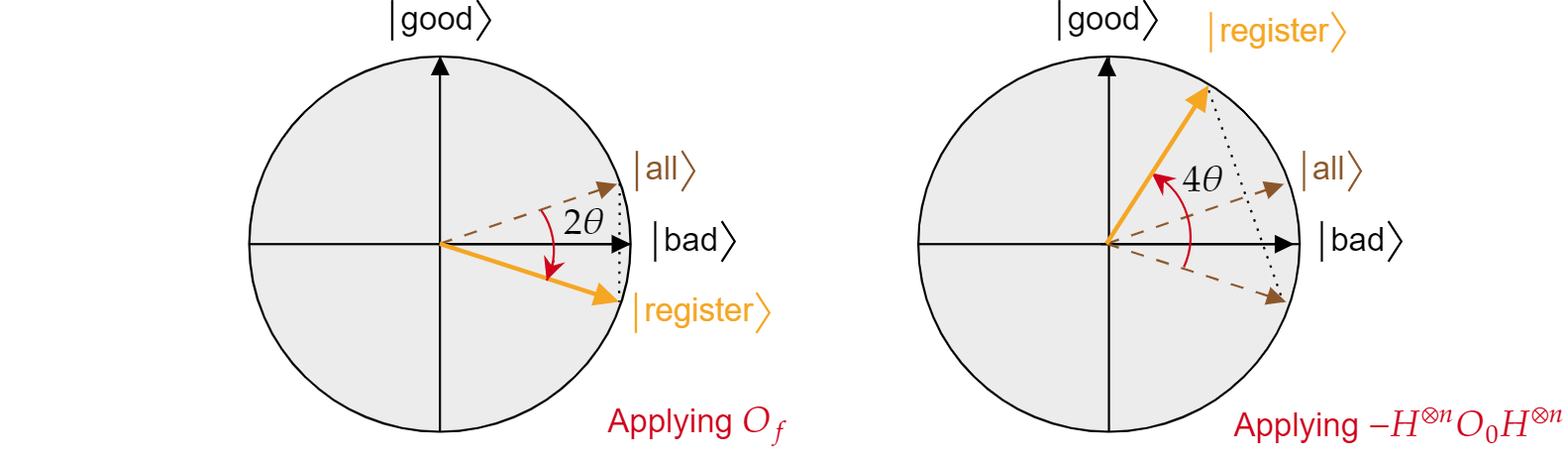
每个 Grover 迭代产生的综合效应是逆时针旋转的角度 $2\theta$。 幸运的是,这个角度 $\theta$ 很容易找到。 由于 $\theta$ 只是 $\ket{\text{all}}$ 和 $\ket{\text{bad}}$ 之间的角度,可以使用标量积找到角度。 已知 $\cos{\theta}=\braket{\text{all}|\text{bad}}$,因此需要计算 $\braket{\text{all}|\text{bad}}$。 通过 $\ket{\text{all}}$ 对 $\ket{\text{bad}}$ 和 $\ket{\text{good}}$ 的分解,推断出:
$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
寄存器的状态与 $\ket{\text{良好}}$ 状态之间的角度随每次迭代而减少,从而产生更高的测量有效结果的概率。 若要计算此概率,只需计算 $|\braket{\text{良好的}|\text{寄存器}}|^2$。 $\ket{\text{good}}$ 和 $\ket{\text{register}}$ 之间的角度表示为 $\gamma (k)$,其中 $k$ 是迭代计数:
$\gamma = \frac{\pi}{2}-\theta -2k\theta =\frac{\pi}{{2} -(2k + 1) \theta $
因此,成功的概率是:
$$P(\text{success}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
最佳迭代次数
由于成功概率可以表示为迭代次数的函数,因此,可通过计算使成功概率函数(接近)最大化的最小正整数,找到最佳的迭代次数 $N_{\text{optimal}}$。
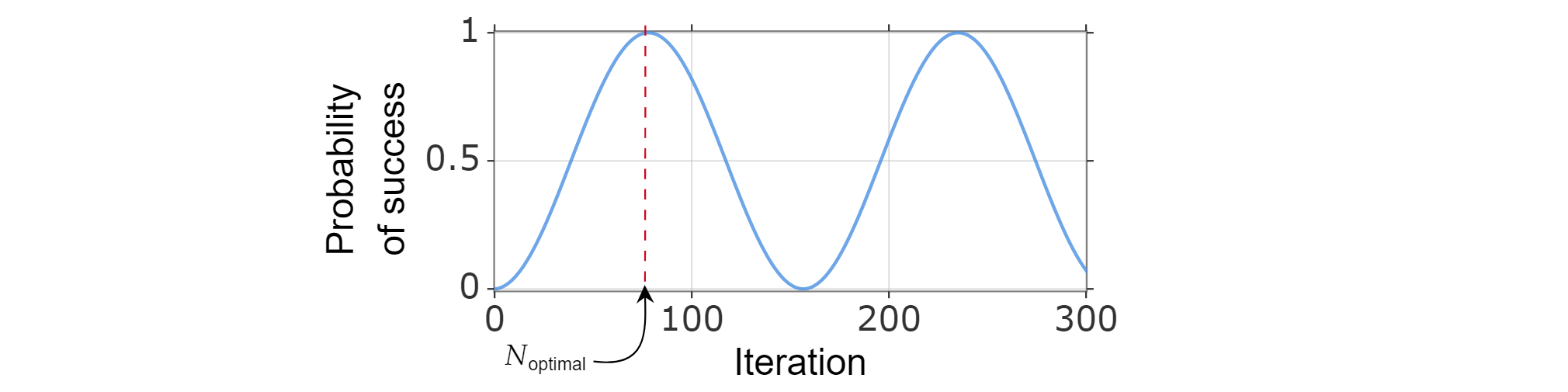
已知 $x{\pi}$ 时,$\sin^2=\frac{x}{2}$ 达到其第一个最大值,因此:
$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$
会得到:
$$k_{\text{optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2 =\frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N}\right)$$
在最后一步中,$\arccos \sqrt{1-x}=\sqrt{x} + O(x^{3/2})$。
因此,你可以选择 $N_{\text{optimal}}=\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-\frac{{1}{{2}\right\rfloor$。
复杂度分析
通过前面的分析,需要查询黑盒 $O_f\left\sqrt{\frac{O}{(}}\rightN$M$)$ 次才能找到有效的项。 不过,就时间复杂度而言,此算法能否有效实现? $O_0$ 基于计算对 $n$ 比特的布尔运算,已知可使用 $O(n)$ 个门实现。 还有两层 $n$ 阿达马门。 因此这两个部分每次迭代只需要 $O(n)$ 个门。 由于 $N=2^n$,可推断出 $O(n)=O(log(N))$。 这样的话,如果需要 $O\left(\sqrt{\frac{N}{M}}\right)$ 次迭代,并且每次迭代需要 $O(log(N))$ 个门,总时间复杂度(不考虑黑盒实现)为 $O\left(\sqrt{\frac{N}{M}}log(N)\right)$。
算法的总体复杂性最终取决于 oracle $O_f$实现的复杂性。 如果函数计算在量子计算机上比经典计算复杂得多,那么整体算法运行时在量子情况下会更长,尽管从技术上而言,它使用的查询更少。
参考
若要继续了解 Grover 算法,可以访问以下资源:
- Lov K. Grover 的原创论文
- 尼尔森的量子搜索算法部分, M. A. &放大 器;庄,洛杉矶(2010年)。 《量子计算和量子信息》。
- Arxiv.org 上的 Grover 算法