Intro to Audio Programming, Part 1: How Audio Data is Represented

The Black Art of Audio Programming

I feel like I’ve got a pretty good handle on most aspects of programming – algorithms, databases, business logic, etc. One area of programming that has always baffled me is audio. I know what sound waves look like, but I never understood how that pretty graph in your audio editor somehow represents a tone, or a song, or what have you.

I was recently presented with a challenge that caused me to dig a little deeper in this area and find out more about how digital sound works.

How Sound Works

Sound in the physical world is pretty straightforward. You are in some kind of medium that can transmit waves, like open air or even water. (Sound cannot exist in places where there is no medium, like a vacuum, i.e. outer space, because there is no air or anything to disturb). When something happens that makes a sound, a longitudinal wave emanates from that place in all directions. This wave causes changes in the pressure in that medium.

So, if I clap in a room full of air, my clap causes these waves of pressure to occur. When those waves hit my eardrums, my brain interprets them as sound.

Check out this article for a more detailed explanation of how sound works in the physical world.

Digital Audio

When you look at an audio file in an audio editor, you see a graph known as a waveform. This represents the entire sound wave for that chunk of audio.

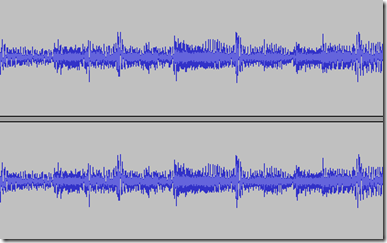
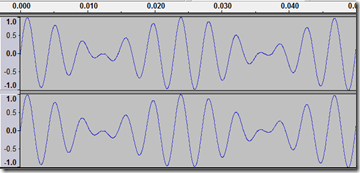
The screenshot below should be a familiar sight. It is part of the waveform for some random song on my hard drive:

Note there are two waveforms here. This is because the file has two channels of audio, making it a stereo recording. Mono recordings only have one channel.

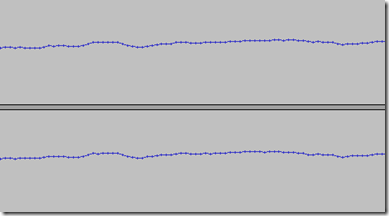
If you were to play all of this audio, you would hear part of a song. However, let’s zoom in considerably:

Wait, what’s this? It’s just a connected series of points! And if you were to play this tiny, tiny segment of the waveform, you would most likely not hear anything at all, save for perhaps a click or two. What is going on here??

Anatomy of Digital Audio

Each data point you see in that second screenshot is called a sample. The sample is simply the amplitude of the wave at that miniscule point in time.

There are literally thousands of these things in a single second of audio. The number of samples per second in an audio file is known as the sampling rate and usually falls somewhere around 44,100 samples per second (written as 44,100 Hz or 44.1 kilohertz). A higher sampling rate means more data points per second, and consequently, higher fidelity audio. Other common sampling rates are 48 KHz, 96 KHz, 192KHz, 8KHz and anywhere in between. If you are recording audio at 44.1 KHz, you will have 44,100 separate data points for each second of recorded audio, and that is a LOT of data points. This huge abundance of data is very close to capturing continuous data.

So because we zoomed in so far on that second screenshot, you are only hearing the measurement of the wave for a tiny, tiny fraction of a second, which is too fast to be audible anyway. The datapoints themselves are not what make the sound, but rather the overall change in these thousands of datapoints over a much longer time.

Similarly, if your audio was just a singe oscillation of a sine wave, you would not hear anything. You would have to hear many of them together in very rapid succession to hear anything reminiscent of a tone.

This brings me to the topic of frequency.

Fundamental Frequency

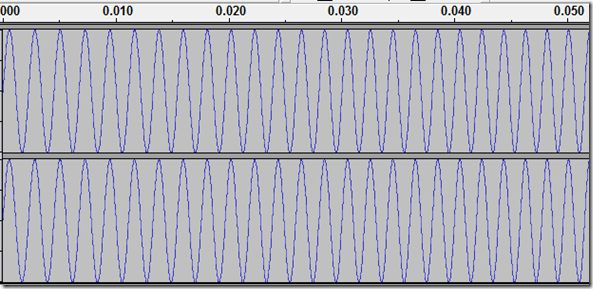
Let’s have a look at a sine wave:

Look how many oscillations we have here, in only 0.05 seconds of audio!!

The number of oscillations of the wave per second is called the fundamental frequency of the tone. If the sine wave oscillates 440 times in a second, you will hear a pitch widely recognized as ‘Concert A (440 Hz)’. In this same screenshot, if we were looking at a 200Hz wave, the oscillations would be spaced farther apart and the tone would be lower. If we were looking at a 1200Hz wave, the oscillations would be closer together and the tone would be higher.

Each time you see a crest in that wave, it is a high-amplitude, high-air-pressure moment. The faster these high pressure moments come at your ears, the higher the perceived pitch will be. But the valleys are important too, because without the reduction in pressure, there is no change in pressure at all for your eardrums to notice. Because the sine wave is the smoothest curve we can generate, the resulting tone is also the mellowest-sounding to the ears (whereas a square wave is rather harsh, and a sawtooth wave is somewhere in between).

The video below shows how the faster you hear a particular sound repeated, the higher the pitch of the resulting tone becomes.

Explanation of Frequency in Digital Audio from Dan Waters on Vimeo.

Bit Depth

The amplitude of the wave at a given point is usually measured in decibels. However, the range and potential resolution of amplitude is impacted by how fine the measurement of an individual sample is. In an 8-bit waveform, you have 8 bits to define a sample. In 16-bit audio, you have 16 bits to define that same sample, so a much more detailed representation of sound is possible. The higher the bit depth, the better the sound quality (and the larger the resulting file size).

More Than Sine Waves

Obviously, songs are more interesting than just a single sine wave. That’s because when you break down the final mix of a song, it’s still just a wave – it causes your speakers to create very minute and rapid disturbances in the air based on changes in amplitude of the wave.

Multiple Tones

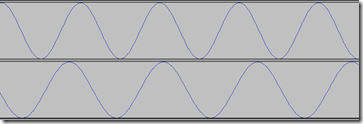
So, let’s take a look at a two-channel mix of a Concert C sine wave (261.25 Hz) and the A below concert C (440 Hz). Together, you hear a very sad-sounding A-minor dyad. Notice the difference in the period of the two waves. Because this is two-channel audio, you hear two sine waves at different frequencies, giving you a dual tone effect.

Of course, there aren’t many songs out there that just have one voice in each channel. The instruments are all mixed together and deliberately placed in the left or right side of the mix, and the mixing process takes care of how the audio is weighted across the two stereo channels.

You can add these two waves together just by taking the average of both sine waves at each point. The resulting stereo waveform looks like this, and you hear both frequencies played at the same time in both channels:

Conclusion

Now you know the basics of how sound waves work. In the next article, we will explore how to synthesize a sine wave using C# into a WAV file.

Currently Playing: Spin Doctors - Pocket Full Of Kryptonite - Off My Line

Comments

• Anonymous
  June 22, 2009
  The comment has been removed

• Anonymous
  June 29, 2009
  A small detail, the usual sampling rate, the one we use in our Audio-CDs, is 44.1 KHz, that means 44,100 Hz.

• Anonymous
  July 01, 2009
  The comment has been removed

• Anonymous
  July 02, 2009
  Fascinating post, thank you! I've always wondered what exactly these funny audio waveforms are all about. Now I know :)  Look forward to reading the rest of your posts on the subject as well.

• Anonymous
  July 03, 2009
  The comment has been removed

• Anonymous
  August 25, 2009
  You've explained sound related concepts pretty nicely, thanks a lot !

• Anonymous
  April 27, 2011
  Great Article! I need some links to coding audio in C++

• Anonymous
  October 24, 2011
  I love the conceptual perspective. I wish more professors would teach subjects conceptually. Thanks for great article!

• Anonymous
  March 17, 2012
  thanks for this ...i wanted to know about this for a long time

• Anonymous
  February 01, 2013
  what is audio programming software?

• Anonymous
  February 28, 2015
  "This huge abundance of data is very close to capturing continuous data.". Isn't any finite number of samples still infinitely small compared to "continuous data" ?

• Anonymous
  September 06, 2015
  Wow.  Great article.  Have been wanting someone to do some sound programming for me as I have no expertise in this.  However, am wanting to do some research in clinical effects of sound.  I need some programming for sounds in a resonance chamber e.g., sounds coming from center of chamber back to listener after bouncing off walls.  Any help available?