Awesome F# - Decision Trees – Part II
In my previous post I went over the theory behind the ID3 algorithm. Now that we got all that painful math out of the way, let’s write some code! Here is an implementation of the algorithm in F#. (It is also attached to this blog post, download it via the link at the bottom.)
open System
type Record =
{
Outlook : string
Temperature : string
Humidity : string
Wind : string
PlayTennis : bool
}
/// Given an attribute name return its value
member this.GetAttributeValue(attrName) =
match attrName with
| "Outlook" -> this.Outlook
| "Temperature" -> this.Temperature
| "Humidity" -> this.Humidity
| "Wind" -> this.Wind
| _ -> failwithf "Invalid attribute name '%s'" attrName
/// Make the %o format specifier look all pretty like
override this.ToString() =
sprintf
"{Outlook = %s, Temp = %s, Humidity = %s, Wind = %s, PlayTennis = %b}"
this.Outlook
this.Temperature
this.Humidity
this.Wind
this.PlayTennis
type DecisionTreeNode =
// Attribute name and value / child node list
| DecisionNode of string * (string * DecisionTreeNode) seq
// Decision and corresponding evidence
| Leaf of bool * Record seq
// ----------------------------------------------------------------------------
/// Return the total true, total false, and total count for a set of Records
let countClassifications data =
Seq.fold
(fun (t,f,c) item ->
match item.PlayTennis with
| true -> (t + 1, f, c + 1)
| false -> (t, f + 1, c + 1))
(0, 0, 0)
data
// ----------------------------------------------------------------------------
/// Return the theoretical number of bits required to classify the information.
/// If a 50/50 mix, returns 1, if 100% true or false returns 0.
let entropy data =
let (trueValues, falseValues, totalCount) = countClassifications data
let probTrue = (float trueValues) / (float totalCount)
let probFalse = (float falseValues) / (float totalCount)
// Log2(1.0) = infinity, short circuiting this part
if trueValues = totalCount || falseValues = totalCount then
0.0
else
-probTrue * Math.Log(probTrue, 2.0) + -probFalse * Math.Log(probFalse, 2.0)
/// Given a set of data, how many bits do you save if you know the provided attribute.
let informationGain (data : Record seq) attr =
// Partition the data into new sets based on each unique value of the given attribute
// e.g. [ where Outlook = rainy ], [ where Outlook = overcast], [ ... ]
let divisionsByAttribute =
data
|> Seq.groupBy(fun item -> item.GetAttributeValue(attr))
let totalEntropy = entropy data
let entropyBasedOnSplit =
divisionsByAttribute
|> Seq.map(fun (attributeValue, rowsWithThatValue) ->
let ent = entropy rowsWithThatValue
let percentageOfTotalRows = (float <| Seq.length rowsWithThatValue) / (float <| Seq.length data)
-1.0 * percentageOfTotalRows * ent)
|> Seq.sum
totalEntropy + entropyBasedOnSplit
// ----------------------------------------------------------------------------
/// Give a list of attributes left to branch on and training data,
/// construct a decision tree node.
let rec createTreeNode data attributesLeft =
let (totalTrue, totalFalse, totalCount) = countClassifications data
// If we have tested all attributes, then label this node with the
// most often occuring instance; likewise if everything has the same value.
if List.length attributesLeft = 0 || totalTrue = 0 || totalFalse = 0 then
let mostOftenOccuring =
if totalTrue > totalFalse then true
else false
Leaf(mostOftenOccuring, data)
// Otherwise, create a proper decision tree node and branch accordingly
else
let attributeWithMostInformationGain =
attributesLeft
|> List.map(fun attrName -> attrName, (informationGain data attrName))
|> List.maxBy(fun (attrName, infoGain) -> infoGain)
|> fst
let remainingAttributes =
attributesLeft |> List.filter ((<>) attributeWithMostInformationGain)
// Partition that data base on the attribute's values
let partitionedData =
Seq.groupBy
(fun (r : Record) -> r.GetAttributeValue(attributeWithMostInformationGain))
data
// Create child nodes
let childNodes =
partitionedData
|> Seq.map (fun (attrValue, subData) -> attrValue, (createTreeNode subData remainingAttributes))
DecisionNode(attributeWithMostInformationGain, childNodes)
The entropy and informationGain functions were covered in my last post, so let’s walk through how the actual decision tree gets constructed. There’s a little work to calculating the optimal decision tree split, but with F# you can express it quite beautifully.
let attributeWithMostInformationGain =
attributesLeft
|> List.map(fun attrName -> attrName, (informationGain data attrName))
|> List.maxBy(fun (attrName, infoGain) -> infoGain)
|> fst
First, it takes all the potential attributes left to split on…
attributesLeft
… and then maps that attribute name to a new attribute name / information gain tuple …
|> List.map(fun attrName -> attrName, (informationGain data attrName))
… then from the newly generated list, pick out the tuple with the highest information gain …
|> List.maxBy(fun (attrName, infoGain) -> infoGain)
…finally returning the first element of that tuple, which is the attribute with the highest information gain.
|> fst
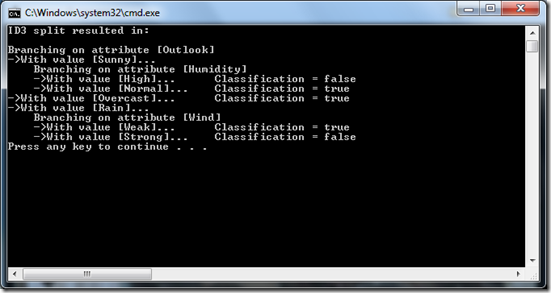
Once you can construct a decision tree in memory, how do get it out? The simplest way is to print it to the console.
The code is very straight forward. Note the use of ‘padding parameter’, so that recursive calls get indented more and more. This is a very helpful technique when printing tree-like data structures to the console.
/// Print the decision tree to the console
let rec printID3Result indent node =
let padding = new System.String(' ', indent)
match node with
| Leaf(classification, data) ->
printfn "\tClassification = %b" classification
// data |> Seq.iter (fun item -> printfn "%s->%s" padding <| item.ToString())
| DecisionNode(attribute, childNodes) ->
printfn "" // Finish previous line
printfn "%sBranching on attribute [%s]" padding attribute
childNodes
|> Seq.iter (fun (attrValue, childNode) ->
printf "%s->With value [%s]..." padding attrValue
printID3Result (indent + 4) childNode)
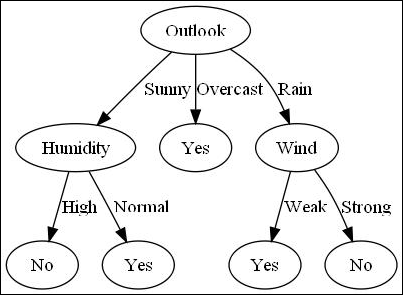
However, it’s almost the year 2010. So in lieu of flying cars perhaps we can at least do better than printing data to the console. Ideally, we want to generate some sexy image like this:
You could painstakingly construct the decision tree using Microsoft Visio but fortunately there are tools to do this for you. AT&T Research has produced a great tool called GraphViz. While the end result doesn’t quite have sizzle, it’s very easy enough to get going.
The following function dumps the decision tree into a format that GraphViz can plot. (Just copy the printed text into the tool and plot it using the default settings.)
/// Prints the tree in a format amenable to GraphViz
/// See https://www.graphviz.org/ for more format
let printInGraphVizFormat node =
let rec printNode parentName name node =
match node with
| DecisionNode(attribute, childNodes) ->
// Print the decision node
printfn "\"%s\" [ label = \"%s\" ];" (parentName + name) attribute
// Print link from parent to this node (unless it's the root)
if parentName <> "" then
printfn "\"%s\" -> \"%s\" [ label = \"%s\" ];" parentName (parentName + name) name
childNodes
|> Seq.iter(fun (attrValue, childNode) ->
printNode (parentName + name) attrValue childNode)
| Leaf(classification, _) ->
let label =
match classification with
| true -> "Yes"
| false -> "No"
// Print the decision node
printfn "\"%s\" [ label = \"%s\" ];" (parentName + name) label
// Print link from parent to this node
printfn "\"%s\" -> \"%s\" [ label = \"%s\" ];" parentName (parentName + name) name
printfn "digraph g {"
printNode "" "root" node
printfn "}"
So there you have it, ID3 in F#. With a little bit of mathematics and some clever output you can construct decision trees for all your machine learning needs. Think of the ID3 algorithm in the future the next time you want to mine customer transactions, analyze server logs, or program your killer robot to find Sarah Conner.
<TotallyShamelessPlug> If you would like to learn more about F#, check out Programming F# by O’Reilly. Available on Amazon and at other fine retailers. </TotallyShamelessPlug>
Comments
Anonymous
November 02, 2009
If you explicitly set the fontsize to say 12, you won't get that annoying clipping of the bottom of the text of the "Outlook"-node. For example like so: printfn "digraph g {" printfn " graph [fontsize=12]" printfn " node [fontsize=12]" printfn " edge [fontsize=12]" printNode "" "root" node printfn "}"Anonymous
November 03, 2009
Thanks for the tip, I'll try to update the image late tonight. I know there enough options in GraphViz to make it prettier, I just didn't spend the time to learn them.Anonymous
November 20, 2009
Thanks for taking the time to write an informative post. Unfortunately, the link to the previous article appears not to point to the right place - I found the right article in the end, but it's a little confusing.