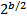Implementing uniqueness constraints on large columns

SQL Server uniqueness constraints create an underlying unique index. SQL Server index keys may not be more than 900 bytes. Below I discuss how to implement uniqueness constraints with hash indexes when the key size can exceed 900 bytes and give the results of some tests on the relative performance of the hash index approach.

Calculating the size of an index

If there are variable length columns, SQL Server may allow the uniqueness constraint to be created but oversized rows will not be insertable. Below is a formula to determine when an index may overflow the 900 byte limit. The maximum size of a unique constraint index key can be calculated using Table 1 as:

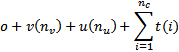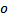 where  is the overhead,  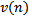is the variable sized column overhead for  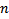variable sized columns,  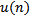is the nullable column overhead for  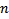nullable columns,  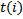is the type cost for column 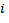,  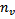is the number of variable sized columns, 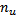is the number of nullable columns and  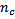is the number of columns. The overhead  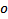varies depending on whether or not the underlying index is clustered (see Table 1).

Table 1 Table of contributions to the size of an index key. To calculate the maximum size of an index key in bytes add the size of every column in the index key and the primary key and add the overhead.

 

Object	Size (bytes)
bigint	8
binary(n)
binary(max)
bit	1
char
date	3
datetime	8
datetime2	8
datetimeoffset	10
decimal	17
float	8
geography
geometry
hierarchyid	892
image
int	4
money	8
nchar(n)
nchar(max)
ntext
numeric	17
nvarchar(n)
nvarchar(max)
real	4
smalldatetime	4
smallint	2
smallmoney	4
sql_variant	8016
sysname	256
text
time	5
timestamp	8
tinyint	1
uniqueidentifier	16
varbinary
varbinary(max)
varchar
xml
CLR type	?
variable size columns (n)	(0 if n = 0)
nullable columns (n)	(0 if n = 0)
clustered overhead	4
nonclustered overhead	7

Using hash indexes to enforce uniqueness constraints

If the index key will always be 900 bytes or less, then an ordinary uniqueness constraint may be used. If the index key could be greater than 900 bytes, then a uniqueness constraint can be enforced with an after-trigger. To avoid table scans, a hash index can be generated for the columns with the unique constraint. The uniqueness constraint can be enforced with the scheme:

create table [Schema].[Table]
(
  [Id]      int not null constraint [PK_Table] primary key,
  …,
  [Column₁] Column₁TypeDeclaration not null,
  [Column₂] Column₂TypeDeclaration null,
  …,
  [Internal_Hash_Column₁_Column₂] as checksum([Column₁], [Column₂]) persisted not null
);
go

create index [Unique_Hash_Table_Column₁_Column₂] on [Schema].[Table] ([Internal_Hash_Column₁_Column₂]);
go

create trigger [ConstraintInsertTrigger_Extent] on [Schema].[Table]
  after of insert, update as
begin
  if (update([Column₁]) or update([Column₂])) and
exists (select *
from [Schema].[Table] as T
inner join inserted as I on I.[Internal_Hash_Column₁_Column₂] = T. [Internal_Hash_Column₁_Column₂] and
I.[Column₁] = T.[Column₁] and
(I.[Column₂] = T.[Column₂] or (I.[Column₂] is null and T.[Column₂] is null))
group by I.[Internal_Hash_Column₁_Column₂], I.[Column₁], I.[Column₂]
having count(*) > 1)
 begin
  if @@trancount > 0
begin
rollback transaction;
end;

raiserror(N'Error: Values in the columns [Schema].[Table] ([Column₁], [Column₂]) must be unique.', 16, 0);
  end;
end;
go

Essentially, the strategy is to store an indexed hash of the columns in the uniqueness constraint. The after trigger makes sure there are no duplicates, by searching for rows that both hash to the same value as one of the inserted rows and match on the constrained columns. Using hashes avoids scanning the entire table for matches and has good space efficiency. The above scheme shows how to handle multiple columns and both nullable and non-nullable columns.

The reason to use checksum and neither hashbytes nor binary_checksum is that checksum respects collation. For example,

checksum(N'X') = checksum(N'x')

but

binary_checksum(N'X') ≠ binary_checksum(N'x').

However, hashbytes and binary_checksum are suitable hashing functions for non-text columns. Also if the constrained columns are unlikely to contain common prefixes, a prefix of the columns (e.g. left([Column], 10)) may be a very good hashing function.

Using a uniqueness constraint on a hashed column to enforce uniqueness constraints

A common alternative strategy is to put a unique constraint over a persisted column defined using hashbytes. The idea is that the chance of a collision for, say, a SHA1 hash is so low that other bugs or hardware failures are much more likely to cause a failure. However, because of the Birthday Fallacy/Paradox people often underestimate the chance of a collision happening. If a hashing function is perfect then the chance of there being a collision among n randomly chosen values in a b-bit hash is approximately:

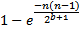In general, a collision is highly likely in a sample of size

Thus for, say, the 160 bit SHA1 hash the chance of a collision in even a trillion random rows seems very low. However, there are some flaws in this argument:

· Cryptographic hashing functions are poorly understood but there are strong indications that MD5 and SHA1 are weaker than perfect hashing functions.

· For a given value, it is often feasible to find another value that hashes to the same hash (i.e. a hash collision). Thus if an application could be compromised by a hash collision and an adversary has some control over the values the application uses then this strategy is unsuitable.

· Cryptographic hash functions do not respect collations. Thus, two strings that are equal like ‘X’ and ‘x’ (in a case insensitive collation) may hash to different hashes.

· The input to the hashing function is usually not random.

Relative performance of the hash index approach for columns under 900 bytes

It seems likely that the hash index approach is more efficient than the unique index based approach at enforcing uniqueness constraints. Table 2 and Table 3 show the average time to insert and delete 1 000 and 100 000 rows for various sized strings with a uniqueness constraint. The SQL Server unique constraint and the hash index approach are compared for both the no prefix and the 20 byte (10 Unicode character) common prefix cases. From this analysis, it is clear that for column sets under 900 bytes the hash index approach is unlikely to perform better than a traditional unique index based approach. The test was carried out on a dedicated workstation with an Intel Pentium D 3.00GHz processor and 4 GB of RAM. The test script is attached to this blog entry.

Table 2: The average time, in seconds, to insert and delete 1 000 rows with a Unicode string with a uniqueness constraint. Both the unique and hash index approaches to uniqueness constraint enforcement are tabulated. Both random strings and strings with a fixed 20 byte (10 Unicode character) prefix are tabulated. The first time in each pair, is the time to insert 1 000 rows at once. The second time in each pair, is the time to insert 1 000 rows separately (i.e. 1 at a time).

	Unique index				Hash index
Length	No prefix		With prefix		No prefix		With prefix
50	0.10	0.43	0.11	0.46	0.12	0.59	0.12	0.59
100	0.18	0.45	0.18	0.44	0.14	0.58	0.14	0.57
200	0.26	0.56	0.26	0.54	0.28	0.62	0.24	0.60
400	0.37	0.62	0.39	0.66	0.31	0.65	0.42	0.70

Table 3: The average time, in seconds, to insert and delete 100 000 rows with a Unicode string with a uniqueness constraint. Both the unique and hash index approaches to uniqueness constraint enforcement are tabulated. Both random strings and strings with a fixed 20 byte (10 Unicode character) prefix are tabulated. The first time in each pair, is the time to insert 100 000 rows at once. The second time in each pair, is the time to insert 100 000 rows separately (i.e. 1 at a time).

	Unique index				Hash index
Length	No prefix		With prefix		No prefix		With prefix
50	6.71	36.22	6.92	35.05	20.82	52.60	20.54	60.33
100	7.09	37.36	7.33	37.02	39.92	57.03	36.14	57.46
200	16.38	43.13	15.01	44.09	65.81	59.12	62.35	59.55
400	33.59	55.07	24.99	56.63	149.95	70.06	151.21	71.07

Large uniqueness constraints.docx