Vectors, vertices, and quaternions
Throughout Direct3D, vertices describe position and orientation. Each vertex in a primitive is described by a vector that gives its position, color, texture coordinates, and a normal vector that gives its orientation.
Quaternions add a fourth element to the [x, y, z] values that define a three-component-vector. Quaternions are an alternative to the matrix methods that are typically used for 3D rotations. A quaternion represents an axis in 3D space and a rotation around that axis. For example, a quaternion might represent a (1,1,2) axis and a rotation of 1 radian. Quaternions carry valuable information, but their true power comes from the two operations that you can perform on them: composition and interpolation.
Performing composition on quaternions is similar to combining them. The composition of two quaternions is notated like the following illustration.
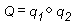
The composition of two quaternions applied to a geometry means "rotate the geometry around axis₂ by rotation₂, then rotate it around axis₁ by rotation₁." In this case, Q represents a rotation around a single axis that is the result of applying q₂, then q₁ to the geometry.
Using quaternion interpolation, an application can calculate a smooth and reasonable path from one axis and orientation to another. Therefore, interpolation between q₁ and q₂ provides a simple way to animate from one orientation to another.
When you use composition and interpolation together, they provide you with a simple way to manipulate a geometry in a manner that appears complex. For example, imagine that you have a geometry that you want to rotate to a given orientation. You know that you want to rotate it r₂ degrees around axis₂, then rotate it r₁ degrees around axis₁, but you don't know the final quaternion. By using composition, you could combine the two rotations on the geometry to get a single quaternion that is the result. Then, you could interpolate from the original to the composed quaternion to achieve a smooth transition from one to the other.
Related topics
Coordinate systems and geometry