Konvolutionella neurala nätverk
Även om du kan använda djupinlärningsmodeller för alla typer av maskininlärning är de särskilt användbara för att hantera data som består av stora matriser med numeriska värden , till exempel bilder. Maskininlärningsmodeller som fungerar med bilder är grunden för ett område med artificiell intelligens som kallas , och djupinlärningstekniker har varit ansvariga för att driva fantastiska framsteg på detta område under de senaste åren.
Kärnan i djupinlärningens framgång på detta område är en typ av modell som kallas ett konvolutionellt neuralt nätverk, eller CNN. En CNN fungerar vanligtvis genom att extrahera funktioner från bilder och sedan mata in dessa funktioner i ett fullständigt anslutet neuralt nätverk för att generera en förutsägelse. Extraheringsskikten för funktioner i nätverket har effekten att minska antalet funktioner från den potentiellt enorma matrisen med enskilda pixelvärden till en mindre funktionsuppsättning som stöder etikettförutsägelse.
Lager i en CNN
CNN består av flera lager, där var och en utför en specifik uppgift för att extrahera funktioner eller förutsäga etiketter.
Konvolutionslager
En av huvudskikttyperna är ett convolutional lager som extraherar viktiga funktioner i bilder. Ett convolutional-lager fungerar genom att tillämpa ett filter på bilder. Filtret definieras av en kernel- som består av en matris med viktvärden.
Ett 3x3-filter kan till exempel definieras så här:
1 -1 1
-1 0 -1
1 -1 1
En bild är också bara en matris med pixelvärden. För att använda filtret applicerar du det på en bild och beräknar en viktad summa av de motsvarande bildpixelvärdena under filterkärnan. Resultatet tilldelas sedan till mittencellen för en motsvarande 3x3-ruta i en ny matris med värden med samma storlek som bilden. Anta till exempel att en bild på 6 x 6 har följande pixelvärden:
255 255 255 255 255 255
255 255 100 255 255 255
255 100 100 100 255 255
100 100 100 100 100 255
255 255 255 255 255 255
255 255 255 255 255 255
Att tillämpa filtret på den övre vänstra 3x3-delen av bilden fungerar så här:
255 255 255 1 -1 1 (255 x 1)+(255 x -1)+(255 x 1) +
255 255 100 x -1 0 -1 = (255 x -1)+(255 x 0)+(100 x -1) + = 155
255 100 100 1 -1 1 (255 x1 )+(100 x -1)+(100 x 1)
Resultatet tilldelas motsvarande pixelvärde i den nya matrisen så här:
? ? ? ? ? ?
? 155 ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
Nu flyttas filtret (konvolvera), vanligtvis med hjälp av ett steg på storlek 1 (så att man flyttar en pixel åt höger), och värdet för nästa pixel beräknas.
255 255 255 1 -1 1 (255 x 1)+(255 x -1)+(255 x 1) +
255 100 255 x -1 0 -1 = (255 x -1)+(100 x 0)+(255 x -1) + = -155
100 100 100 1 -1 1 (100 x1 )+(100 x -1)+(100 x 1)
Så nu kan vi fylla i nästa värde för den nya matrisen.
? ? ? ? ? ?
? 155 -155 ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
En process upprepas tills vi har tillämpat filtret på alla 3x3-rutor av bilden för att skapa en ny matris med värden som ser ut så här:
? ? ? ? ? ?
? 155 -155 155 -155 ?
? -155 310 -155 155 ?
? 310 155 310 0 ?
? -155 -155 -155 0 ?
? ? ? ? ? ?
På grund av filterkärnans storlek kan vi inte beräkna värden för bildpunkterna vid kanten. så vi använder vanligtvis bara en utfyllnad värde (ofta 0):
0 0 0 0 0 0
0 155 -155 155 -155 0
0 -155 310 -155 155 0
0 310 155 310 0 0
0 -155 -155 -155 0 0
0 0 0 0 0 0
Utdata från convolution skickas vanligtvis till en aktiveringsfunktion, som ofta är en ReLU-funktion (Rectified Linear Unit) som säkerställer att negativa värden anges till 0:
0 0 0 0 0 0
0 155 0 155 0 0
0 0 310 0 155 0
0 310 155 310 0 0
0 0 0 0 0 0
0 0 0 0 0 0
Den resulterande matrisen är en funktionskarta med funktionsvärden som kan användas för att träna en maskininlärningsmodell.
Obs: Värdena på funktionskartan kan vara större än det maximala värdet för en pixel (255), så om du vill visualisera funktionskartan som en bild måste du normalisera funktionsvärdena mellan 0 och 255.
Konvolutionsprocessen visas i animationen nedan.

- En bild skickas till det konvolutionella lagret. I det här fallet är bilden en enkel geometrisk form.
- Bilden består av en matris med pixlar med värden mellan 0 och 255 (för färgbilder är detta vanligtvis en 3-dimensionell matris med värden för röda, gröna och blå kanaler).
- En filterkärna initieras vanligtvis med slumpmässiga vikter (i det här exemplet har vi valt värden för att markera effekten som ett filter kan ha på pixelvärden, men i en riktig CNN genereras de initiala vikterna vanligtvis från en slumpmässig gaussisk fördelning). Det här filtret används för att extrahera en funktionskarta från bilddata.
- Filtret är sammanräknat i bilden och beräknar funktionsvärden genom att tillämpa en summa av vikterna multiplicerat med motsvarande pixelvärden i varje position. En rektifierad aktiveringsfunktion för linjär enhet (ReLU) tillämpas för att säkerställa att negativa värden är inställda på 0.
- Efter sammandragningen innehåller funktionskartan de extraherade funktionsvärdena, som ofta framhäver viktiga visuella attribut för bilden. I det här fallet markerar funktionskartan kanterna och hörnen på triangeln i bilden.
Vanligtvis tillämpar ett convolutional-lager flera filterkärnor. Varje filter skapar en annan funktionskarta och alla funktionskartor skickas till nästa lager i nätverket.
Poollager
Efter att ha extraherat egenskapsvärden från bilder används poolningslager (eller nedsamplingslager) för att minska antalet egenskapsvärden samtidigt som de viktiga differentierande egenskaperna som har extraherats bevaras.
En av de vanligaste typerna av pooler är maximal poolning där ett filter tillämpas på bilden, och endast det maximala pixelvärdet i filterområdet behålls. Om du till exempel tillämpar en 2x2-poolningskärna på följande del av en bild skulle resultatet bli 155.
0 0
0 155
Observera att effekten av 2x2-poolfiltret är att minska antalet värden från 4 till 1.
Precis som med konvolutionella lager fungerar poolskikt genom att tillämpa filtret över hela funktionens karta. Animeringen nedan visar ett exempel på maximal poolning för en bildkarta.

- Funktionskartan som extraheras av ett filter i ett convolutional-lager innehåller en matris med funktionsvärden.
- En poolkärna används för att minska antalet funktionsvärden. I det här fallet är kernelstorleken 2x2, så den kommer att producera en array med en fjärdedel av antalet funktionsvärden.
- Poolkärnan konvolveras över funktionskartan och behåller endast det högsta pixelvärdet i varje position.
Ta bort lager
En av de svåraste utmaningarna i en CNN är att undvika överanpassning, där den resulterande modellen presterar bra med träningsdata men inte generaliserar bra till nya data som den inte tränades på. En teknik som du kan använda för att minimera överanpassning är att inkludera lager där träningsprocessen slumpmässigt eliminerar (eller "droppar") funktionskartor. Detta kan verka kontraintuitivt, men det är ett effektivt sätt att se till att modellen inte lär sig att vara överberoende av träningsbilderna.
Andra tekniker som du kan använda för att minimera överanpassning är att slumpmässigt vända, spegla eller snedställa träningsbilderna för att generera data som varierar mellan träningsepoker.
Platta till lagren
När du har använt konvolutional- och poollager för att extrahera de viktigaste funktionerna i bilderna är de resulterande funktionskartorna flerdimensionella matriser med pixelvärden. Ett plattningslager används för att platta ut egenskapskartor till en vektor med värden som kan användas som input i ett fullständigt anslutet lager.
Helt anslutna lager
Vanligtvis slutar en CNN med ett fullständigt anslutet nätverk där funktionsvärdena skickas till ett indatalager, genom ett eller flera dolda lager, och genererar förutsagda värden i ett utdatalager.
En grundläggande CNN-arkitektur kan se ut ungefär så här:
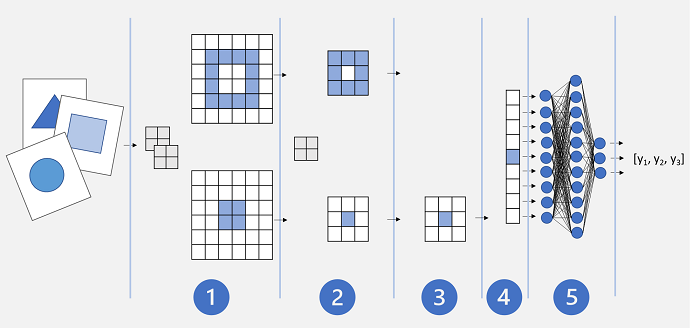
- Bilder matas in i ett konvolutionellt lager. I det här fallet finns det två filter, så varje bild skapar två funktionskartor.
- Funktionskartorna skickas till ett poollager, där en 2x2-poolkärna minskar storleken på funktionskartorna.
- Ett fallande lager släpper slumpmässigt några av funktionsmappningarna för att förhindra överanpassning.
- Ett utplattande lager tar de återstående funktionskartamatriserna och jämnar ut dem till en vektor.
- Vektorelementen matas in i ett helt anslutet nätverk, vilket genererar förutsägelserna. I det här fallet är nätverket en klassificeringsmodell som förutsäger sannolikheter för tre möjliga bildklasser (triangel, kvadrat och cirkel).
Träna en CNN-modell
Som med alla djupa neurala nätverk tränas en CNN genom att skicka batchar med träningsdata genom den över flera epoker, justera vikterna och biasvärdena baserat på förlusten som beräknas för varje epok. När det gäller en CNN innehåller backpropagation av justerade vikter filterkärnvikter som används i konvolutionala lager samt de vikter som används i helt anslutna skikt.