Begrepp för djupt neuralt nätverk
Innan vi utforskar hur du tränar en DNN-maskininlärningsmodell (Deep Neural Network) ska vi fundera på vad vi försöker uppnå. Maskininlärning handlar om att förutsäga en etikett baserat på vissa funktioner i en viss observation. Enkelt uttryckt är en maskininlärningsmodell en funktion som beräknar y (etiketten) från x (funktionerna): f(x)=y.
Ett enkelt klassificeringsexempel
Anta till exempel att din observation består av vissa mätningar av en pingvin.

Mer specifikt är måtten:
- Längden på pingvinens räkning.
- Djupet av pingvinens räkning.
- Längden på pingvinens flipper.
- Pingvinens vikt.
I det här fallet är funktionerna (x) en vektor med fyra värden, eller matematiskt x=[x1,x 2,x 3,x 4].
Låt oss anta att etiketten vi försöker förutsäga (y) är pingvinarten, och att det finns tre möjliga arter det kan vara:
- Adelie
- Gentoo
- Chinstrap
Detta är ett exempel på ett klassificeringsproblem , där maskininlärningsmodellen måste förutsäga den mest sannolika klass som observationen tillhör. En klassificeringsmodell åstadkommer detta genom att förutsäga en etikett som består av sannolikheten för varje klass. Med andra ord är y en vektor med tre sannolikhetsvärden; en för var och en av de möjliga klasserna: y=[P(0),P(1),P(2)].
Du tränar maskininlärningsmodellen med hjälp av observationer som du redan känner till den sanna etiketten för. Du kan till exempel ha följande funktionsmått för ett Adelie-prov :
x=[37.3, 16.8, 19.2, 30.0]
Du vet redan att detta är ett exempel på en Adelie (klass 0), så en perfekt klassificeringsfunktion bör resultera i en etikett som anger 100 % sannolikhet för klass 0 och en sannolikhet på 0 % för klasserna 1 och 2:
y=[1, 0, 0]
En djup neural nätverksmodell
Så hur skulle vi använda djupinlärning för att skapa en klassificeringsmodell för pingvinklassificeringsmodellen? Låt oss titta på ett exempel:
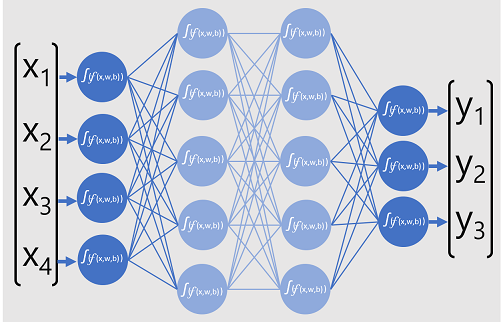
Den djupa neurala nätverksmodellen för klassificeraren består av flera lager av artificiella neuroner. I det här fallet finns det fyra lager:
- Ett indatalager med en neuron för varje förväntat indatavärde (x).
- Två så kallade dolda lager, som var och en innehåller fem neuroner.
- Ett utdatalager som innehåller tre neuroner – ett för varje klasss sannolikhetsvärde (y) som ska förutsägas av modellen.
På grund av nätverkets skiktade arkitektur kallas den här typen av modell ibland för en flerskiktsperceptron. Observera dessutom att alla neuroner i indata och dolda lager är anslutna till alla neuroner i de efterföljande lagren - detta är ett exempel på ett helt anslutet nätverk.
När du skapar en modell som den här måste du definiera ett indatalager som stöder antalet funktioner som din modell ska bearbeta och ett utdatalager som återspeglar antalet utdata som du förväntar dig att den ska producera. Du kan bestämma hur många dolda lager du vill inkludera och hur många neuroner som finns i var och en av dem; men du har ingen kontroll över in- och utdatavärdena för dessa lager – dessa bestäms av modellträningsprocessen.
Träna ett djupt neuralt nätverk
Träningsprocessen för ett djupt neuralt nätverk består av flera iterationer, så kallade epoker. För den första epoken börjar du med att tilldela slumpmässiga initieringsvärden för värdena vikt (w) och bias b. Sedan är processen följande:
- Funktioner för dataobservationer med kända etikettvärden skickas till indataskiktet. I allmänhet grupperas dessa observationer i batchar (kallas ofta minibatch).
- Neuronerna tillämpar sedan sin funktion, och om det aktiveras skickar du resultatet till nästa lager tills utdataskiktet genererar en förutsägelse.
- Förutsägelsen jämförs med det faktiska kända värdet och mängden varians mellan de förutsagda och sanna värdena (som vi kallar förlusten) beräknas.
- Baserat på resultaten beräknas reviderade värden för vikter och biasvärden för att minska förlusten, och dessa justeringar backpropageras till neuronerna i nätverksskikten.
- Nästa epok upprepar batchträningen framåtpass med de reviderade vikt- och biasvärdena, vilket förhoppningsvis förbättrar modellens noggrannhet (genom att minska förlusten).
Kommentar
Bearbetning av träningsfunktionerna som en batch förbättrar effektiviteten i träningsprocessen genom att bearbeta flera observationer samtidigt som en matris med funktioner med vektorer av vikter och fördomar. Linjära algebraiska funktioner som fungerar med matriser och vektorer finns också i 3D-grafikbearbetning, varför datorer med grafiska bearbetningsenheter (GPU: er) ger betydligt bättre prestanda för djupinlärningsmodellträning än endast datorer med central bearbetningsenhet (CPU).
En närmare titt på förlustfunktioner och backpropagation
I den tidigare beskrivningen av djupinlärningsprocessen nämndes att förlusten från modellen beräknas och används för att justera vikt- och biasvärdena. Hur fungerar det här?
Beräkna förlust
Anta att ett av exemplen som skickas genom träningsprocessen innehåller funktioner i ett Adelie-prov (klass 0). Rätt utdata från nätverket skulle vara [1, 0, 0]. Anta nu att utdata som genereras av nätverket är [0.4, 0.3, 0.3]. Genom att jämföra dessa kan vi beräkna en absolut varians för varje element (med andra ord hur långt varje förutsagt värde är borta från vad det ska vara) som [0,6, 0,3, 0,3].
Eftersom vi faktiskt hanterar flera observationer aggregerar vi vanligtvis variansen , till exempel genom att placera de enskilda variansvärdena och beräkna medelvärdet, så vi får ett enda genomsnittligt förlustvärde, till exempel 0,18.
Optimerare
Här är den smarta biten. Förlusten beräknas med hjälp av en funktion som fungerar på resultaten från det sista lagret i nätverket, som också är en funktion. Det sista skiktet av nätverket fungerar på utdata från föregående lager, som också är funktioner. Så i själva verket är hela modellen från indataskiktet direkt till förlustberäkningen bara en stor kapslad funktion. Funktioner har några riktigt användbara egenskaper, bland annat:
- Du kan konceptualisera en funktion som en ritad linje som jämför dess utdata med var och en av dess variabler.
- Du kan använda differentiell kalkyl för att beräkna funktionens derivat när som helst med avseende på dess variabler.
Vi tar den första av dessa funktioner. Vi kan rita raden i funktionen för att visa hur ett enskilt viktvärde jämförs med förlust och markera på den raden den punkt där det aktuella viktvärdet matchar det aktuella förlustvärdet.
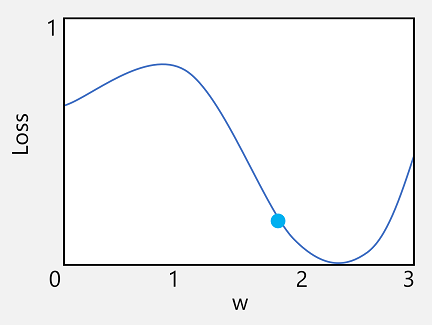
Nu ska vi tillämpa den andra egenskapen för en funktion. Derivatet av en funktion för en viss punkt anger om lutningen (eller toningen) av funktionsutdata (i det här fallet förlust) ökar eller minskar med avseende på en funktionsvariabel (i det här fallet viktvärdet). Ett positivt derivat indikerar att funktionen ökar och ett negativt derivat indikerar att den minskar. I det här fallet har funktionen en nedåtriktad toning vid den ritade punkten för det aktuella viktvärdet. Med andra ord, att öka vikten kommer att ha effekten att minska förlusten.
Vi använder en optimerare för att tillämpa samma trick för alla vikt- och biasvariabler i modellen och bestämma i vilken riktning vi behöver justera dem (upp eller ned) för att minska den totala mängden förlust i modellen. Det finns flera vanliga optimeringsalgoritmer, inklusive stochastic gradient descent (SGD), Adaptive Learning Rate (ADADELTA), Adaptive Momentum Estimation (Adam) och andra, som alla är utformade för att ta reda på hur man justerar vikter och fördomar för att minimera förlusten.
Inlärningstakt
Nu är den uppenbara nästa frågan, med hur mycket ska optimeraren justera vikterna och biasvärdena? Om du tittar på diagrammet för vårt viktvärde kan du se att öka vikten med en liten mängd kommer att följa funktionslinjen nedåt (minska förlusten), men om vi ökar den med för mycket börjar funktionslinjen gå upp igen, så vi kan faktiskt öka förlusten. och efter nästa epok kan vi finna att vi behöver minska vikten.
Storleken på justeringen styrs av en parameter som du anger för utbildning som kallas inlärningshastighet. En låg inlärningsfrekvens resulterar i små justeringar (så det kan ta fler epoker för att minimera förlusten), medan en hög inlärningstakt resulterar i stora justeringar (så du kan missa minimumet helt och hållet).