Vad är klassificering?

Slutförd

Binär klassificering är klassificering med två kategorier. Vi kan till exempel märka patienter som icke-diabetiker eller diabetiker.

Klassförutsägelse görs genom att fastställa sannolikheten för varje möjlig klass som ett värde mellan 0 (omöjligt) och 1 (vissa). Den totala sannolikheten för alla klasser är alltid 1, eftersom patienten definitivt är antingen diabetiker eller icke-diabetiker. Så om den förväntade sannolikheten för att en patient är diabetiker är 0,3, finns det en motsvarande sannolikhet på 0,7 att patienten är icke-diabetiker.

Ett tröskelvärde, ofta 0,5, används för att fastställa den förutsagda klassen. Om den positiva klassen (i det här fallet diabetiker) har en förutsagd sannolikhet som är större än tröskelvärdet, förutsägs en klassificering av diabetiker.

Träna och utvärdera en klassificeringsmodell

Klassificering är ett exempel på en övervakad maskininlärningsteknik, vilket innebär att den förlitar sig på data som innehåller kända funktionsvärden och kända etikettvärden . I det här exemplet är funktionsvärdena diagnostiska mätningar för patienter, och etikettvärdena är en klassificering av icke-diabetiker eller diabetiker. En klassificeringsalgoritm används för att anpassa en delmängd av data till en funktion som kan beräkna sannolikheten för varje klassetikett från funktionsvärdena. Återstående data används för att utvärdera modellen genom att jämföra de förutsägelser den genererar från funktionerna till de kända klassetiketterna.

Ett enkelt exempel

Nu ska vi utforska ett exempel som hjälper dig att förklara de viktigaste principerna. Anta att vi har följande patientdata, som består av en enda funktion (blodsockernivå) och en klassetikett 0 för icke-diabetes, 1 för diabetiker.

Blodglukos	Diabetisk
82	0
92	0
112	1
102	0
115	1
107	1
87	0
120	1
83	0
119	1
104	1
105	0
86	0
109	1

Vi använder de första åtta observationerna för att träna en klassificeringsmodell, och vi börjar med att rita blodglukosfunktionen (x) och den förutsagda diabetesetiketten (y).

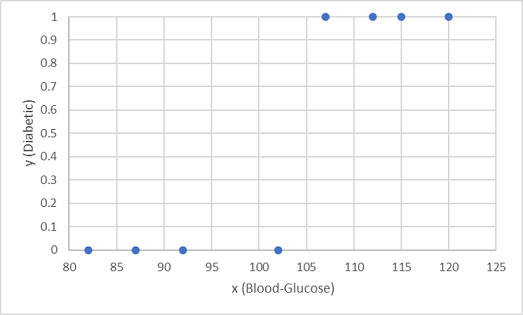
Vad vi behöver är en funktion som beräknar ett sannolikhetsvärde för y baserat på x (med andra ord behöver vi funktionen f(x) = y). Du kan se från diagrammet att patienter med låg blodsockernivå alla är icke-diabetiker, medan patienter med en högre blodsockernivå är diabetiker. Det verkar som ju högre blodsockernivån är, desto mer troligt är det att en patient är diabetiker, med böjningspunkten någonstans mellan 100 och 110. Vi måste anpassa en funktion som beräknar ett värde mellan 0 och 1 för y till dessa värden.

En sådan funktion är en logistisk funktion, som bildar en sigmoidal (S-formad) kurva.

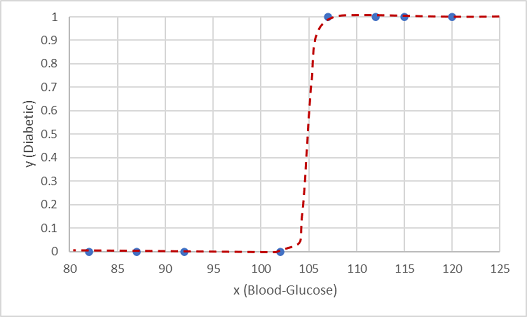
Nu kan vi använda funktionen för att beräkna ett sannolikhetsvärde som y är positivt, vilket innebär att patienten är diabetiker, från valfritt värde av x genom att hitta punkten på funktionslinjen för x. Vi kan ange ett tröskelvärde på 0,5 som brytpunkt för klassetikettförutsägelse.

Vi testar det med de två datavärden som vi höll tillbaka.

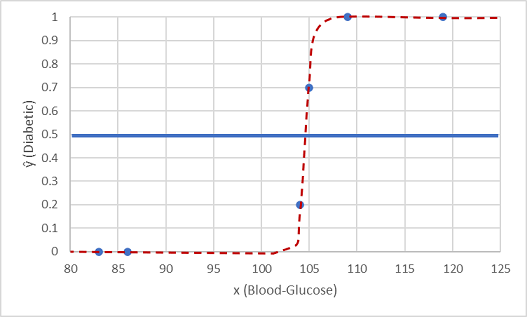
Punkter som ritas under tröskelvärdet ger en förutsagd klass på 0 (icke-diabetiker) och punkter ovanför linjen förutspås som 1 (diabetiker).

Nu kan vi jämföra etikettförutsägelserna (ŷ eller "y-hat"), baserat på den logistiska funktion som är inkapslad i modellen, med de faktiska klassetiketterna (y).

x	y	ŷ
83	0	0
119	1	1
104	1	0
105	0	1
86	0	0
109	1	1