Analysera klassificering med egenskapskurvor för mottagaroperator

  • 4 minuter

Klassificeringsmodeller måste tilldela ett exempel till en kategori. Den måste till exempel använda funktioner som storlek, färg och rörelse för att avgöra om ett objekt är en vandrare eller ett träd.

Vi kan förbättra klassificeringsmodeller på många sätt. Vi kan till exempel se till att våra data är balanserade, rena och skalade. Vi kan också ändra vår modellarkitektur och använda hyperparametrar för att pressa ut så mycket prestanda som möjligt ur våra data och vår arkitektur. Så småningom hittar vi inget bättre sätt att förbättra prestanda på vårt test (eller hålla ut) set och deklarera vår modell redo.

Modelljustering till den här punkten kan vara komplex, men vi kan använda ett sista enkelt steg för att ytterligare förbättra hur bra vår modell fungerar. För att förstå detta måste vi dock gå tillbaka till grunderna.

Sannolikheter och kategorier

Många modeller har flera beslutssteg, och det sista är ofta bara ett binariseringssteg. Under binariseringen konverteras sannolikheter till en hård etikett. Anta till exempel att modellen har funktioner och beräknar att det finns en 75%-chans att den visades som vandrare och 25 % chans att den visades ett träd. Ett objekt får inte vara 75 % vandrare och 25 % träd. Det är det ena eller det andra! Därför tillämpar modellen ett tröskelvärde som normalt är 50 %. Eftersom vandrarklassen är större än 50 % deklareras objektet vara en vandrare.

Tröskelvärdet på 50 % är logiskt. det innebär att den mest sannolika etiketten enligt modellen alltid väljs. Om modellen är partisk kanske det här tröskelvärdet på 50 % inte är lämpligt. Om modellen till exempel har en liten tendens att plocka träd mer än vandrare och plocka träd 10 % oftare än den borde, kan vi justera vårt beslutströskelvärde för att ta hänsyn till detta.

Uppdatera om beslutsmatriser

Beslutsmatriser är ett bra sätt att bedöma vilka typer av misstag en modell gör. Detta ger oss frekvenser av sanna positiva (TP), sanna negativa (TN), falska positiva (FP) och falska negativa (FN)

Diagram som visar en förvirringsmatris med sanna positiva identifieringar, sanna negativa identifieringar, falska positiva identifieringar och falska negativa värden.

Vi kan beräkna några praktiska egenskaper från förvirringsmatrisen. Två populära egenskaper är:

  • True Positive Rate (sensitivity): hur ofta "True"-etiketter identifieras korrekt som "True". Hur ofta modellen till exempel förutsäger "vandrare" när exemplet visas är i själva verket en vandrare.
  • False Positive Rate (false alarm rate): how often "False" labels are incorrectly identified as "True". Till exempel hur ofta modellen förutsäger "vandrare" när det visas ett träd.

Att titta på sanna positiva och falska positiva priser kan hjälpa oss att förstå en modells prestanda.

Tänk på vårt vandrareexempel. Helst är den sanna positiva frekvensen mycket hög och den falska positiva hastigheten är mycket låg, eftersom det innebär att modellen identifierar vandrare väl och inte identifierar träd som vandrare så ofta. Men om den sanna positiva frekvensen är mycket hög, men den falska positiva frekvensen också är mycket hög, är modellen partisk; det identifierar nästan allt det möter som vandrare. På samma sätt vill vi inte ha en modell med låg sann positiv hastighet, för när modellen stöter på en vandrare märker den dem som ett träd.

ROC-kurvor

ROC-kurvor (Receiver Operator Characteristic) är ett diagram där vi ritar sann positiv hastighet jämfört med falsk positiv hastighet.

ROC-kurvor kan vara förvirrande för nybörjare av två huvudsakliga skäl. Den första orsaken är att nybörjare vet att en modell bara har ett värde för sanna positiva och sanna negativa priser, så ett ROC-diagram måste se ut så här:

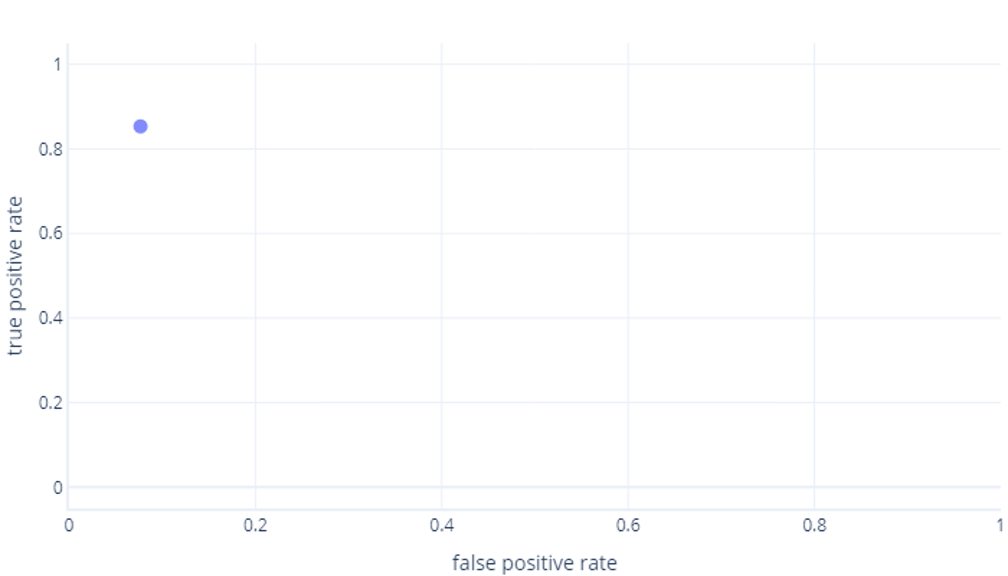
Egenskapskurva för mottagaroperator med en ritpunkt.

Om du också tänker det här, har du rätt. En tränad modell genererar bara en punkt. Kom dock ihåg att våra modeller har ett tröskelvärde – normalt 50 % – som används för att avgöra om etiketten true (hiker) eller false (tree) ska användas. Om vi ändrar tröskelvärdet till 30 % och beräknar om sanna positiva och falska positiva värden får vi en annan punkt:

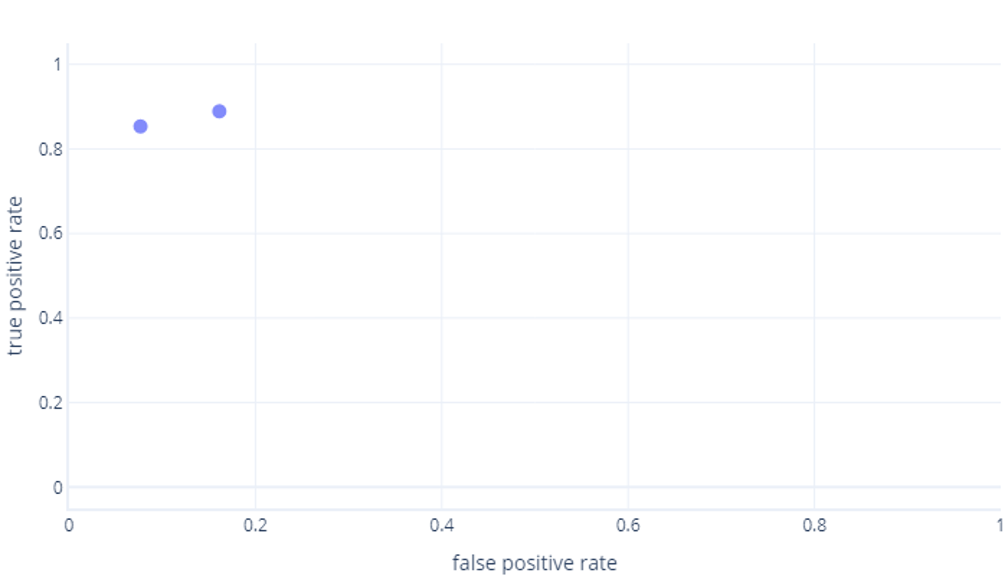
Egenskapskurva för mottagaroperator med två ritpunkter.

Om vi gör detta för tröskelvärden mellan 0%-100 %, kan vi få ett diagram som liknar detta:

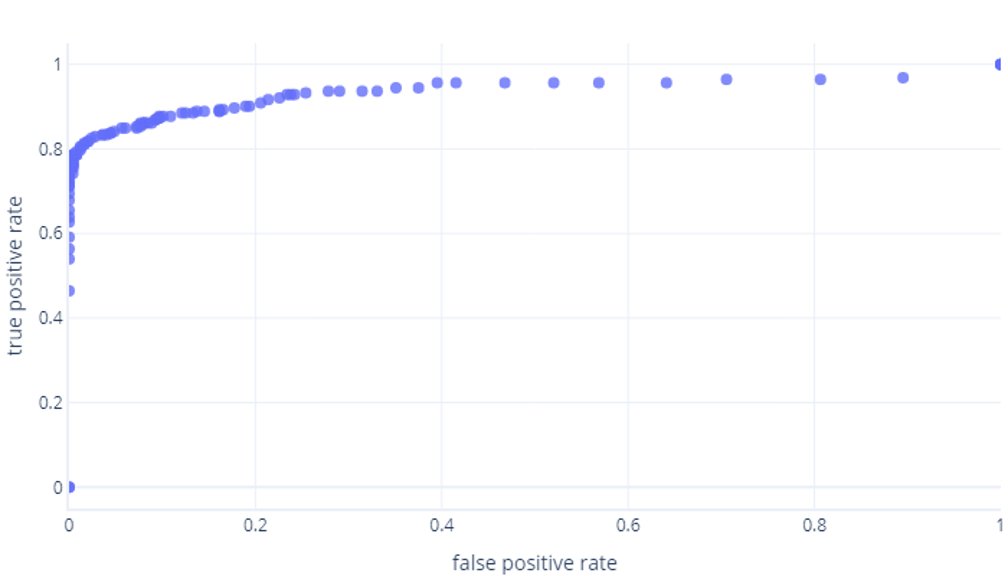
Egenskapskurva för mottagaroperator med en linje med ritpunkter.

Som vi vanligtvis visar som en rad, i stället:

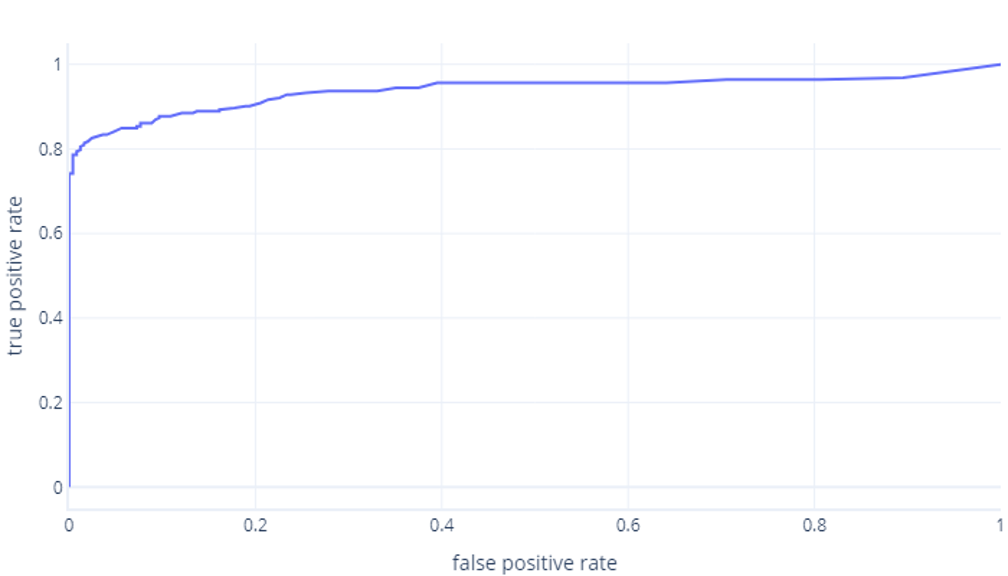
Egenskapskurva för mottagaroperator med en linje i stället för ritpunkter för falska positiva identifieringar.

Den andra anledningen till att dessa grafer kan vara förvirrande är jargongen. Kom ihåg att vi vill ha en hög sann positiv hastighet (identifiera vandrare som sådana) och en låg falsk positiv hastighet (inte identifiera träd som vandrare).

Mottagaroperatorns karakteristiska kurvdiagram med en linje i stället för ritpunkter för att identifiera träd som vandrare.

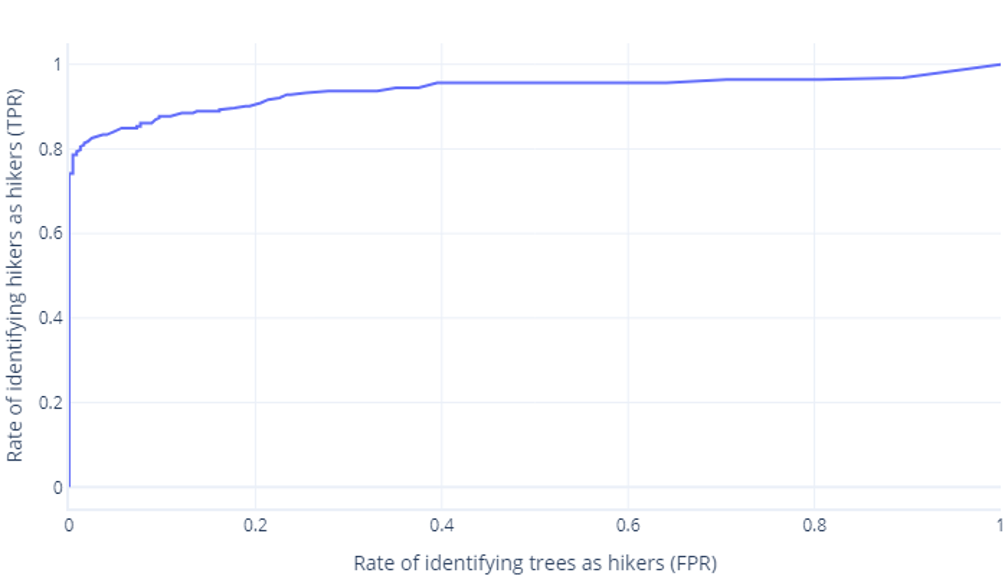
Bra ROC, dålig ROC

Att förstå bra och dåliga ROC-kurvor är något som bäst görs i en interaktiv miljö. När du är redo kan du gå vidare till nästa övning för att utforska det här ämnet.