Beslutsträd och modellarkitektur
När vi pratar om arkitektur tänker vi ofta på byggnader. Arkitekturen ansvarar för hur en byggnad är strukturerad. dess höjd, dess djup, antalet golv och hur saker och ting är anslutna internt. Den här arkitekturen avgör också hur vi använder en byggnad: var vi går in i den och vad vi kan "få ut av den", praktiskt taget.
Inom maskininlärning refererar arkitekturen till ett liknande begrepp. Hur många parametrar har den och hur länkas de samman för att uppnå en beräkning? Beräknar vi mycket parallellt (bredd) eller har vi serieåtgärder som är beroende av en tidigare beräkning (djup)? Hur kan vi tillhandahålla indata till den här modellen och hur kan vi ta emot utdata? Sådana arkitektoniska beslut gäller vanligtvis bara för mer komplexa modeller, och arkitektoniska beslut kan variera från enkla till komplexa. Dessa beslut fattas vanligtvis innan modellen tränas, men i vissa fall finns det utrymme att göra ändringar efter träningen.
Låt oss utforska detta mer konkret med beslutsträd som exempel.
Vad är ett beslutsträd?
I grund och botten är ett beslutsträd ett flödesdiagram. Beslutsträd är en kategoriseringsmodell som delar upp beslut i flera steg.
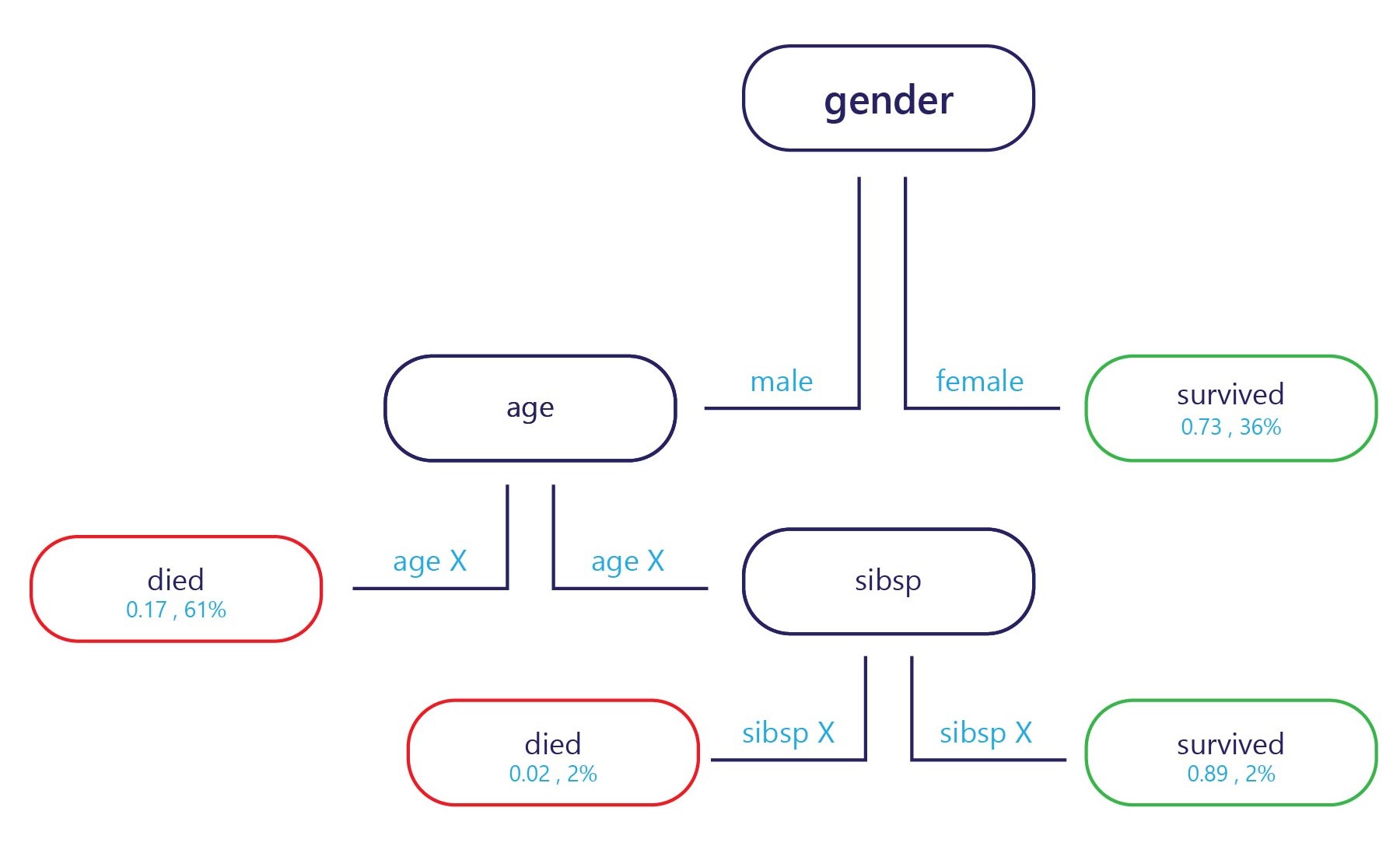
Exemplet om det tillhandahålls vid startpunkten (överst i diagrammet ovan) och varje slutpunkt har en etikett (längst ned i diagrammet). Vid varje nod avgör en enkel "if"-instruktion vilken gren exemplet skickar till nästa. När grenen har nått slutet av trädet (bladen) tilldelas den till en etikett.
Hur tränas beslutsträd?
Beslutsträd tränas en nod eller beslutspunkt i taget. Vid den första noden utvärderas hela träningsuppsättningen. Därifrån väljs en funktion som bäst kan separera uppsättningen i två delmängder som har mer homogena etiketter. Anta till exempel att vår träningsuppsättning var följande:
| Vikt (funktion) | Ålder (funktion) | Vann en medalj (etikett) |
|---|---|---|
| 90 | 18 | Nej |
| 80 | 20 | Nej |
| 70 | 19 | Nej |
| 70 | 25 | Nej |
| 60 | 18 | Ja |
| 80 | 28 | Ja |
| 85 | 26 | Ja |
| 90 | 25 | Ja |
Om vi gör vårt bästa för att hitta en regel för att dela upp dessa data kan vi delas upp efter ålder runt 24 år, eftersom de flesta medaljvinnare var över 24 år. Den här uppdelningen skulle ge oss två delmängder av data.
Delmängd 1
| Vikt (funktion) | Ålder (funktion) | Vann en medalj (etikett) |
|---|---|---|
| 90 | 18 | Nej |
| 80 | 20 | Nej |
| 70 | 19 | Nej |
| 60 | 18 | Ja |
Delmängd 2
| Vikt (funktion) | Ålder (funktion) | Vann en medalj (etikett) |
|---|---|---|
| 70 | 25 | Nej |
| 80 | 28 | Ja |
| 85 | 26 | Ja |
| 90 | 25 | Ja |
Om vi slutar här har vi en enkel modell med en nod och två blad. Leaf 1 innehåller icke-medaljvinnare och är 75% korrekt på vår träningsuppsättning. Leaf 2 innehåller medaljvinnare, och är också 75% korrekt på träningsuppsättningen.
Men vi behöver inte stanna här. Vi kan fortsätta den här processen genom att dela upp bladen ytterligare.
I delmängd 1 kunde den första nya noden delas efter vikt, eftersom den enda medaljvinnaren hade en vikt mindre än personer som inte vann en medalj. Regeln kan vara inställd på "vikt < 65". Personer med vikt < 65 förutspås ha vunnit en medalj, medan alla med vikt ≥65 inte uppfyller detta kriterium och kan förutsägas att inte vinna en medalj.
I delmängd 2 kan den andra nya noden också delas upp efter vikt, men den här gången förutsäger att alla med en vikt över 70 skulle ha vunnit en medalj, medan de under den inte skulle göra det.
Detta skulle ge oss ett träd som skulle kunna uppnå 100 % noggrannhet på träningsuppsättningen.
Styrkor och svagheter i beslutsträd
Beslutsträd anses ha låg bias. Det innebär att de vanligtvis är bra på att identifiera funktioner som är viktiga för att märka något korrekt.
Den största svagheten i beslutsträd är överanpassning. Tänk på exemplet som angavs tidigare: modellen ger ett exakt sätt att beräkna vem som sannolikt kommer att vinna en medalj, och detta förutsäger 100 % av träningsdatauppsättningen korrekt. Den här noggrannhetsnivån är ovanlig för maskininlärningsmodeller, vilket normalt gör många fel på träningsdatauppsättningen. Bra träningsprestanda är inte en dålig sak i sig, men trädet har blivit så specialiserat på träningsuppsättningen att det förmodligen inte kommer att göra bra på testuppsättningen. Detta beror på att trädet har lyckats lära sig relationer i träningsuppsättningen som förmodligen inte är verkliga, till exempel att ha en vikt på 60 kg garanterar en medalj om du är under 25 år gammal.
Modellarkitektur påverkar överanpassning
Hur vi strukturerar vårt beslutsträd är nyckeln till att undvika dess svagheter. Ju djupare trädet är, desto mer sannolikt är det att överanpassa träningsuppsättningen. Om vi till exempel i det enkla trädet ovan endast begränsade trädet till den första noden skulle det göra fel på träningsuppsättningen, men förmodligen göra bättre på testuppsättningen. Detta beror på att det skulle ha mer allmänna regler om vem som vinner medaljer, till exempel "idrottare över 24", snarare än extremt specifika regler som kanske bara gäller för träningsuppsättningen.
Även om vi fokuserar på träd här har andra komplexa modeller ofta liknande svaghet som vi kan minimera genom beslut om hur de är strukturerade eller hur de tillåts manipuleras av träningen.